Ⅰ. Introduction

COORDINATION of multi-agent swarm systems has attracted great interest in recent years. Coordinated movement of fish and formation of birds are two examples of coordination of multi-agent swarm systems in nature. Also,it is known that the swarm behavior of networks of agents has potential applications in various areas (for example in formation control ^{[1, 2]},flocking ^[3] and sensor networks ^[4]). Asymptotic swarm stability,as a general form of consensus,is one of the interesting behaviors in swarm systems. Till now,different studies have been done in this regard ^{[5, 6, 7, 8, 9]}. The dynamic model of agents in most of these studies has been considered in a classical integer order form,whereas the dynamic model of many real-world systems can be better described by fractional order dynamical equations ^{[10, 11]}. Considering this point,study on fractional order swarm systems has attracted much interest in recent years ^{[12, 13, 14, 15, 16, 17, 18, 19, 20]}. For example,these studies include obtaining conditions for coordination in the networked fractional order systems ^[12],time response behavior analysis of agents in asymptotically swarm stable fractional order swarm systems ^[16],controller design for enforcing the agents in uncertain fractional order systems to track a desired trajectory while achieving consensus ^[18],and deriving consensus conditions in the presence of communication time-delays [^[14], ^[19]-^[20]].

In practice,we are faced with different constraints in coordination of multi-agent swarm systems (for example,measurement constraints ^[21],dealing with agents having nonlinear dynamics ^[22],communication constraints ^[23],uncertainty in the dynamical models of the agents ^[24],and time-varying communication links ^[25]). One of the major challenges in the swarm systems is to control the agents when they are exposed to input saturation constraint ^{[26, 27, 28, 29]}. In real-world swarm systems,this constraint is commonly due to physical limitations of the actuators. In this paper,the aim is asymptotic swarm stabilization of fractional order linear time invariant swarm systems subject to input constraints. To clarify the motivation of the paper,let us give an example. Consider a multi-robot system composed of a large number of cooperative mobile robots ^[18]. Assume that the aim of coordination is consensus in such a system ^{[30, 31]}. In some situations,it is more accurate and realistic to model these robots with fractional order differential equations ^{[32, 33]} (for example,when the friction is modeled by the fractional order equations ^{[34, 35]},or when the robots are driven on the sandy or muddy road ^[12]). In these situations,we face a multi-agent system with a fractional order swarm model. Also due to the physical constraints,in these cases the input torque that should be applied to the wheels of the robot for changing the velocity or the orientation is limited. Generally speaking,in the mentioned example the control objective is to achieve consensus in a multi-robot system as a fractional order swarm system where the control inputs are subjected to input constraints. This example clearly verifies the importance of controller design in the presence of control input constraints for achieving consensus in a fractional order swarm system. Considering input saturation constraints,consensus in networked multi-agent systems has been studied in ^{[26, 27, 28, 29]}. But,the dynamics of each agent in these papers is in classical integer order form. Recently, ^[36] has considered input saturation in stability and stabilization of fractional order linear systems. In the present paper,the results of ^[36] are used for proposing a control law for asymptotic swarm stabilization of fractional order swarm systems in the presence of input saturation constraints.

Another constraint is also considered in this paper. More precisely, the other constraint is an assumption that during achieving consensus,all the agents will be inside a specified region and the distance of agents from the final destination is less than a desired value. To reveal the motivation for considering such a constraint in this paper,we again recall the above-mentioned example on consensus in a multi-robot system. In this swarm system,due to the communication and environmental limitations,it may be desirable that the distance between the robots and their final distention is less than a specified value during the reaching consensus. This control objective can be satisfied by considering ,the ,second constraint, in ,the ,controller ,design procedure. In summary,the main contribution of the paper is to propose a feedback controller for asymptotic swarm stabilization of fractional order linear time invariant swarm systems in the presence of the aforementioned constraints.

This paper is organized as follows: The problem formulation and some preliminaries are given in Section Ⅱ. Section Ⅲ presents some properties on linear transformations appeared in our study. The control law for the asymptotic swarm stabilization of fractional order swarm systems with input constraint is obtained in Section Ⅳ. Simulation results in Section Ⅴ are given to confirm the analytical results. Finally,conclusions in Section Ⅵ close the paper.

Ⅱ. Preliminaries A. Notations

The notations used in this paper are fairly standard. ${\bf R}^+$ denotes the set of positive real numbers. sgn $( \cdot )$ and sat $( \cdot )$ respectively indicate the sign and saturation functions. $sym\{X\}$, where $X$ is a real square matrix,denotes the symmetric matrix $X^{\rm T}+X$. ${\rm{diag}}\left\{ {{c_1},{c_2}, \cdots ,{c_n}} \right\}$ specifies a diagonal matrix with diagonal entries ${c_1},{c_2}, \ldots $, and $c_n $. If $z\in {\bf C}$, ${arg(z)}$ denotes the argument of $z$. Also,$I_m$ and $\otimes $ respectively indicate the $m\times m$ identity matrix and the kronecker product operator. $eig(A)$ denotes eigenvalue of the square matrix $A$. $Nu(M)$ and $Ra(M)$ are respectively the null space and the range space of matrix $M$. $\left\| {\mbox{ }\cdot \mbox{ }} \right\|$ and $\left\| {\mbox{ }\cdot \mbox{ }} \right\|_\infty $ specify respectively 2-norm and infinity-norm functions. The distance between vector $e=[e_1 ,e_2 ,\ldots,e_n ]\in {\bf R}^n$ and the non-empty set $S$ is defined by $D(e,S):=\mathop {inf}_{s\in S} \vert \vert e-s\vert \vert $. Moreover,$A_{(i)} $ denotes the $i$-th row of matrix $A\in {\bf R}^{m\times n}$. Finally for the vectors $A_1 ,A_2 ,A_3 \in {\bf R}^n$,the vector inequality $A_1 \le A_2 \le A_3 $ means $A_{1_{(i)}} \le A_{2_{(i)}} \le A_{3_{(i)}} ,i=1,\ldots n$.

B. Fractional Order Linear Time Invariant Swarm Systems

A fractional order linear time invariant swarm system of $N$ agents can be described by ^[16]

\begin{align} D_t^\alpha x_i &=Ax_i +F\sum\limits_{j=1}^N {w_{ij} (x_j -x_i)+B} u_i ,\nonumber \\i&=1,2,\ldots,N. \end{align}

(1)

where $A\in {\bf R}^{d\times d},\quad F\in {\bf R}^{d\times d},_{ }B\in {\bf R}^{d\times m},\quad x_i \in {\bf R}^d,\quad u_i \in {\bf R}^m,$ $w_{ij} \ge 0,$ and $\alpha \in (0,1]$. Also,in (1) $D_t^\alpha $ denotes the Caputo fractional derivative operator defined as follows ^[37].

\begin{align} D_t^\alpha f(t)&=\frac{1}{\Gamma (\left\lceil \alpha \right\rceil -\alpha )}\int_0^{\rm T} {\frac{f^{(\left\lceil \alpha \right\rceil )}(\tau )}{(t-\tau )^{\alpha -\left\lceil \alpha \right\rceil +1}}{\rm d}\tau },\nonumber \\ 0&<\alpha \notin {\bf Z}. \end{align}

(2)

In this swarm system,the communication among agents is described by a weighted graph of order $N$,denoted by $G$,such that each agent is corresponding to a vertex of $G$. This graph may either be directed or undirected. $w_{ij} $ in (1) indicates the weight of the edge between $i$-th and $j$-th agents and can be considered as a measure of data transmission between these two agents ^[38]. The adjacency matrix of graph $G$ is as follows:

\begin{align*} W_G =\left[{{\begin{array}{*{20}c} {w_{11} } & {\ldots} & {w_{1N} } \\ \vdots & \ddots & \vdots \\ {w_{N1} } & \cdots & {w_{NN} } \\ \end{array} }} \right]\nonumber \end{align*}

The concept of asymptotic swarm stability in a swarm system is defined on the basis of the relative distances between the agents ^[38].

Definition 1. (Asymptotic swarm stability) ^[38] The fractional order linear time invariant swarm system in (1) is asymptotically swarm stable if for each $\bar {\varepsilon }>0$ there exists $\bar {T}>0$ such that $\left\| {x_i (t)-x_j (t)} \right\|<\bar {\varepsilon }$ for all $i,j\in \{1,2,\ldots,N\}$ and $t>\bar {T}.$

Considering the pseudo state vector of agents as $x=[x_1^{\rm T} ,\ldots,x_N^{\rm T}]^{\rm T}$,the swarm system in (1) can be rewritten as ^[38]

\begin{align} D_t^\alpha x=(I_N \otimes A-L\otimes F)x+(I_N \otimes B)U, \end{align}

(3)

where $U=[u_1^{\rm T} ,\ldots,u_N^{\rm T}]^{\rm T}$ is the input vector and $L=L(G)$ is the Laplacian matrix of graph $G$ ^[39]. In this paper,the following assumption is considered on communication graph $G$.

Assumption 1. Graph $G$ in swarm system (1) is in one of the following forms:

1) $G$ is an undirected connected graph.

2) $G$ is a directed graph which includes a spanning tree and the eigenvalues of its Laplacian matrix are real numbers.

Let $\lambda _1 =0,\;\lambda _2 ,\ldots,\lambda _N \in {\bf R}^+_{ }$ be the eigenvalues of the Laplacian matrix $L$ of fractional order linear time invariant swarm system in (1) (Considering Assumption 1,the Laplacian matrix $L$ has exactly one zero eigenvalue and its other eigenvalues are positive real ^[5]). Also,assume that the Jordan canonical form of $L_{ }$ is denoted by $J$. This means that there exists a non-singular matrix $T$ such that

\begin{align*} J=TLT^{-1}=\left[{{\begin{array}{*{20}c} 0 & 0 & 0 & \cdots & 0 \\ 0 & {\lambda _2 } & \ast & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \ldots & \ast \\ 0 & 0 & \cdots & 0 & {\lambda _N } \\ \end{array} }} \right], \end{align*}

where "*" may either be 1 or 0. By defining $\tilde {x}=[\tilde {x}_1^{\rm T},\tilde {x}_2^{\rm T},\ldots,\tilde {x}_N^{\rm T} ]^{\rm T}=(T\otimes I_d )x$ and $\tilde {U}=[\tilde {u}_1^{\rm T},\tilde {u}_2^{\rm T},\ldots,\tilde {u}_N^{\rm T}]^{\rm T}=(T\otimes I_m )U$,the swarm system in (3) is rewritten as

\begin{align} D_t^\alpha \tilde {x}=(I_N \otimes A-J\otimes F)\tilde {x}+(I_N \otimes B)\tilde {U}, \end{align}

(4)

where matrix $I_N \otimes A-J\otimes F$ is of the form

\begin{align} &I_N \otimes A-J\otimes F \nonumber \\& =\left[{{\begin{array}{*{20}c} A & 0 & 0 & \cdots & 0 \\ 0 & {A-\lambda _2 F} & \times & \cdots & 0 \\ 0 & \vdots & \vdots & \ddots & \vdots \\ \vdots & 0 & \cdots & \cdots & \times \\ 0 & 0 & \cdots & 0 & {A-\lambda _N F} \\ \end{array} }} \right]\in {\bf R}^{Nd\times Nd}, \end{align}

(5)

and each "$\times $" represents a block in ${\bf R}^{d\times d}$ that may either be $-F$ or 0 ^{[16, 38]}. Also,matrix $I_N \otimes B$ in (4) is expressed as follows.

\begin{align} I_N \otimes B=\left[{{\begin{array}{*{20}c} B & 0 & 0 & \cdots & 0 \\ 0 & B & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \cdots & 0 \\ 0 & 0 & \cdots & 0 & B \\ \end{array}}} \right]\in {\bf R}^{Nd\times Nm}. \end{align}

(6)

The following lemma presents the necessary and sufficient conditions for asymptotic swarm stability of the fractional order swarm system (1) by checking the asymptotic stability of a fractional order linear time invariant system.

Lemma 1. ^[38] The fractional order linear time invariant swarm system (1) with Assumption 1 is asymptotically swarm stable if and only if the following system

\begin{align} D_t^\alpha \hat {x}=\hat {A}\hat {x}+\hat {B}\hat {U}, \end{align}

(7)

is asymptotically stable where $\hat {x}=[\tilde {x}_2^{\rm T} ,\tilde {x}_3^{\rm T} ,\ldots,\tilde {x}_N^{\rm T}]^{\rm T}\in {\bf R}^{(N-1)d}$,$\hat {U}=[\tilde {u}_2^{\rm T} ,\tilde {u}_3^{\rm T} ,\ldots,\tilde {u}_N^{\rm T}]^{\rm T}\in {\bf R}^{(N-1)m}$ and matrices $\hat {A}$ and $\hat {B}$ are defined as follows:

\begin{align} &\hat {A}=\left[{{\begin{array}{*{20}c} {A-\lambda _2 F} & \times & 0 & \cdots & 0 \\ 0 & {A-\lambda _3 F} & \times & \cdots & 0 \\ 0 & \vdots & \vdots & \ddots & \vdots \\ \vdots & 0 & \cdots & \cdots & \times \\ 0 & 0 & \cdots & 0 & {A-\lambda _N F} \\ \end{array} }} \right]\nonumber \\& ~~~~~~\in {\bf R}^{(N-1)d\times (N-1)d} \end{align} \begin{align} &\hat {B}=\left[{{\begin{array}{*{20}c} B & 0 & 0 & \cdots & 0 \\ 0 & B & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \cdots & 0 \\ 0 & 0 & \cdots & 0 & B \\ \end{array} }} \right] & \in {\bf R}^{(N-1)d\times (N-1)m}\nonumber \end{align}

(8)

Although Lemma 1 has been presented in ^[38] for integer order case (i.e. where $\alpha =1)$,its proof can be easily extended to the fractional order case ^[16]. On the other hand,system (7) is asymptotically stable (or equivalently the swarm system (1) with Assumption 1 is asymptotically swarm stable) if and only if the condition $\left| {arg (\lambda )} \right|>\alpha \pi /2$ is satisfied for each eigenvalue $\lambda $ of matrix $\hat {A}$ ^[40]. In such a case,matrix $\hat {A}$ is called an $\alpha $-Hurwitz matrix

C. Problem Statement

In this paper,the aim is asymptotic swarm stabilization of fractional order linear time invariant swarm system (1) under the following constraints:

Constraint 1. The control inputs $u_i, {i}=1,2,\ldots,N,$ in (1) should be bounded as $\left| {u_{i(l)}} \right|\le \bar {u}_{i(l)}$,${i}=1,2,\ldots,N,{l}=1,2,\ldots m$, where $\bar {u}_{i(l)} \in {\bf R}^+$ denotes the allowable upper bound for the $l$-th control input of $i$-th agent.

Constraint 2. The distance between $x(t)=[x_1^{\rm T} (t),\ldots,x_N^{\rm T} (t)]^{\rm T}\in {\bf R}^{Nd}$ and the set $\{x\in {\bf R}^{Nd}\vert x=[x_1^{\rm T} ,\ldots,x_N^{\rm T} ]^{\rm T},\;x_1 =x_2 =\cdots =x_N ,\;x_i \in {\bf R}^d \,(i=1,\ldots,N)\}$ in the $Nd$-dimensional space should be less than $\mu \in {\bf R}^+$ for each $t\ge 0$.

Constraint 1 specifies the input saturation constraints in the fractional order swarm system (1). Actually,this constraint will bound the input signals in (1) similar to the virtual saturation function $sat(u_i) :{\bf R}^m\to {\bf R}^m$ where

\begin{align} sat(u_i )=[sat(u_{i(1)} ),sat(u_{i(2)} ),\ldots,sat(u_{i(m)})]^{\rm T} \end{align}

(9)

and $ sat(u_{i(l)} ),i=1,2,\ldots,N,\mbox{ }l=1,2,\ldots,m $ is defined as follows ^[36].

\begin{align} sat(u_{i(l)})={\rm sgn}(u_{i(l)}){\rm min} (\bar {u}_{i(l)},\left | {u_{i(l)}}\right|). \end{align}

(10)

Also,Constraint 2 states that during reaching consensus the pseudo state vector of agents ($x(t))$ should be inside a specified region. Note that the line $x_1 =x_2 =\cdots =x_N $ expresses a situation in which the pseudo states of all agents are the same. This situation can be interpreted as the "final destination" in the problem of swarm stabilization. In fact,Constraint 2 enforces that during reaching consensus,the distance between agents and this final destination is less than a desired value specified by $\mu $.

Ⅲ. Some Properties of $x\to (QT\otimes I_d )x$

According to the definitions of pseudo-state variables $x=[x_1^{\rm T} ,\ldots,x_N^{\rm T}]^{\rm T}\in {\bf R}^{Nd}$, $\tilde {x}=[\tilde {x}_1^{\rm T} ,\tilde {x}_2^{\rm T} ,\ldots,\tilde {x}_N^{\rm T}]^{\rm T}=(T\otimes I_d )x$,and $\hat {x}=[\tilde {x}_2^{\rm T} ,\tilde {x}_3^{\rm T} ,\ldots,\tilde {x}_N^{\rm T}]^{\rm T}\in {\bf R}^{(N-1)d}$ in the previous section,one can easily obtain the vector $\hat {x}$

\begin{align} \hat{x}=(Q\otimes I_d )(T\otimes I_d )x=(QT\otimes I_d )x, \end{align}

(11)

where

\begin{align} Q=\left[{{\begin{array}{*{20}c} 0 & 1 & 0 & \cdots & 0 \\ \vdots & 0 & \vdots & \ddots & \vdots \\ 0 & \vdots & \vdots & \cdots & 0 \\ 0 & 0 & \cdots & 0 & 1 \\ \end{array} }} \right]_{(N-1)\times N.} \end{align}

(12)

In this section,the linear transformation $x\in {\bf R}^{Nd}\to \hat {x}=(QT\otimes I_d )x\in {\bf R}^{(N-1)d}$ is studied from the viewpoint of geometric properties. We will use these geometric properties to solve the main problem in the next section. At first,consider the following lemma.

Lemma 2. By the linear transformation $x\to \hat {x}=Px$,where $P=QT\otimes I_d $,$T$ is the transition matrix introduced in Section Ⅱ-B and $Q$ is defined as in (12),the closed ball ${\beta _\varepsilon }: = \{ \hat x \in {{\bf{R}}^{(N - 1)d}}|{\hat x^{\rm{T}}}\hat x \le \varepsilon \} $ transforms to the region $\beta _\varepsilon ^\prime : = \{x\in {\bf R}^{Nd}\vert x^{\rm T}zx\le \varepsilon \}$ with $z=P^{\rm T}P$.

Proof. By substituting $\hat {x}$ from (11) in the definition of the closed ball $\beta _\varepsilon $,the region $\beta _\varepsilon ^\prime $ is easily obtained.

It is clear that the center of the closed ball $\beta _\varepsilon $ in Lemma 2 is the origin. According to Lemma 2,the set $\{x\in {\bf R}^{Nd}\vert x^{\rm T}zx=0\}$ specifies all the vectors which are transformed by the aforementioned transformation to the origin. The geometric interpretation of this set is revealed in Lemma 3.

Lemma 3. If $P=QT\otimes I_d $,$z=P^{\rm T}P$,and matrices $T$ and $Q$ are as in Lemma 2,then $\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}=\{x\in {\bf R}^{Nd}\vert x^{\rm T}zx=0\}$.

Proof. To prove this lemma,we show that the set $\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$ is the only solution of the equation $x^{\rm T}zx=0$. The equation $x^{\rm T}zx=0$ can be written as

\begin{align} x^{\rm T}zx=x^{\rm T}P^{\rm T}Px=\left\| {Px} \right\|^2=0, \end{align}

(13)

which is equivalent to

\begin{align} Px=(QT\otimes I_d )x=0. \end{align}

(14)

For simplicity,assume that $d=1$ which results in $I_d =1$ (The proof can be easily extended for $d>1)$. Assuming $I_d =1$ and using(12),(14) can be written as

\begin{align} QTx=\left[{{\begin{array}{*{20}c} {t_{2,1} } & \cdots & {t_{2,N} } \\ \vdots & \ddots & \vdots \\ {t_{N,1} } & \cdots & {t_{N,N} } \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {x_1 } \\ {x_2 } \\ \vdots \\ {x_N }\end{array} }} \right]=0, \end{align}

(15)

where $t_{i,k} $ ($i=2,3,\ldots,N,k=1,2,\ldots,N)$ denotes the elements of similarity matrix $T$. On the other hand,

\begin{align} T\left[{{\begin{array}{*{20}c} {\hat {t}_{11} } \\ {\hat {t}_{11} } \\ \vdots \\ {\hat {t}_{11} } \\ \end{array} }} \right]=\left[{{\begin{array}{*{20}c} 1 \\ 0 \\ \vdots \\ 0 \\ \end{array} }} \right], \end{align}

(16)

where $[\hat {t}_{11} ,\ldots,\hat {t}_{11}]^{\rm T}$ is the first column of matrix $T^{-1}$ ^{[16, 18]}. Equation (16) means that the sum of all entries in each row (except the first row) of matrix $T$ is zero,i.e. $\sum_{k=1}^N {t_{i,k} =\mbox{ }0,\mbox{i}=2,3,\ldots,N} $. As a result,according to (15),it is easy to conclude that each member of the set $\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$ is a solution for equation (13). Also,according to the independent linearity of the rows of the matrix $T$,the rank of matrix $QT$ in (15) is $N-1$. So,the set $\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$ specifies all of the solutions of equation (13).

To express a geometric property for the region $\beta _\varepsilon ^\prime $ introduced in Lemma 2,some preliminary lemmas are needed. These lemmas (Lemmas 4-6) are as follows.

Lemma 4 ^[41] Let $\bar {G}\in {\bf R}^{n\times n}$ and $\bar {H}\in {\bf R}^{m\times m}$ be two arbitrary matrices and have singular values (eigenvalues) $\sigma _i ,i=1,2,\ldots,n$ and $\mu _j \mbox{,}j=1,2,\ldots,m$ respectively. Then,the $mn$ singular values (eigenvalues) of matrix $\bar {G}\otimes \bar {H}$ are as follows.

\begin{align} \sigma _1 \mu _1 ,\ldots,\sigma _1 \mu _m ,\mbox{ }\sigma _2 \mu _1 ,\ldots,\sigma _2 \mu _m ,\mbox{ }\ldots\mbox{ },\sigma _n \mu _1 ,\ldots,\sigma _n \mu _m. \end{align}

(17)

Lemma 5. If $S:= {S}'\otimes I_d $,where matrix ${S}'$ is defined as

\begin{align} {S}'=\left[{{\begin{array}{*{20}c} {N-1} & {-1} & \cdots & {-1} \\ {-1} & {N-1} & \ddots & \vdots \\ \vdots & \vdots & \cdots & {-1} \\ {-1} & \cdots & {-1} & {N-1} \\ \end{array} }} \right]\in {\bf R}^{N\times N}, \end{align}

(18)

then

\begin{align} \left\| S \right\|=N. \end{align}

(19)

Proof. It can be verified that the characteristic polynomial of matrix ${S}'$ is

\begin{align} \det (\lambda I-{S}')=\lambda (\lambda -N)^{N-1}. \end{align}

(20)

From (20),${S}'$ has one zero eigenvalue,and the other eigenvalues of this matrix are equal to $N$. Therefore,the maximum singular value of real symmetric matrix ${S}'$ or equivalently its 2-norm is $N$.

Lemma 6. Let $\rho _{\min } $ denote the minimum singular value of matrix $QT$ where $T$ is the transition matrix introduced in Section Ⅱ-B and $Q$ is defined by (12). In this case,

\begin{align} \left\| {Sx} \right\|\le \frac{N}{\rho _{\min } }\left\| {Px} \right\|,\quad \forall x\in {\bf R}^{Nd}, \end{align}

(21)

where matrices $P$ and $S$ are respectively defined in Lemmas 2 and 5.

Proof. In the proof of Lemma 3,it is verified that $Nu(P)=\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$. On the other hand,by considering the structure of matrix ${S}'$ in (18) and noting $S={S}'\otimes I_d $ it is deduced that $Nu(S)=\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$. Therefore,subspaces $Nu(S)$ and $Nu(P)$ are identical,and consequently,the orthogonal complements of these subspaces (i.e.,$Ra(S^{\rm T})$ and $Ra(P^{\rm T}))$ are also identical. Now,by the range-null space decomposition of ${\bf R}^{Nd}$ ^[42],each $x\in {\bf R}^{Nd}$ can be uniquely written as $x=x_{Nu} +x_{Ra} $ where $x_{Nu} \in Nu(S)=Nu(P)=\{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$ and $x_{Ra} \in Ra(S^{\rm T})=Ra(P^{\rm T})$. Since $Sx_{Nu} =0$,for each $x\in {\bf R}^{Nd}$ decomposed in the form $x=x_{Nu} +x_{Ra} $ we have

\begin{align} \left\| {Sx} \right\|=\left\| {Sx_{Ra} } \right\|. \end{align}

(22)

Let us define the new matrix $\hat {P}$ as follows:

\begin{align} \hat {P}=(Q^{\rm T}QT)\otimes I_d. \end{align}

(23)

Considering the structures of matrices $Q$ and $QT$ from (12) and (15),it is deduced that matrix $Q^{\rm T}QT$ is in the form

\begin{align} Q^{\rm T}QT=\left[{{\begin{array}{*{20}c} 0 & \cdots & 0 \\ {t_{2,1} } & \cdots & {t_{2,N} } \\ \vdots & \ddots & \vdots \\ {t_{N,1} } & \cdots & {t_{N,N} } \\ \end{array} }} \right]. \end{align}

(24)

As discussed in the proof of Lemma 3,we know that $\sum_{k=1}^N {t_{i,k} =\mbox{ }0,\mbox{ }i=2,3,\ldots,N} $. According to this equality,nonsingularity of matrix $T,$ and structure of matrix $Q^{\rm T}QT$ in (24),it is found that $\hat {P}x_{Nu} =0$ if and only if $x_{Nu} \in \{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$. Hence,$Nu(\hat {P})=Nu(S)=Nu(P)$,$Ra(\hat {P})=Ra(S)=Ra(P)$, and for each $x\in {\bf R}^{Nd}$ decomposed as $x=x_{Nu} +x_{Ra} $, we have

\begin{align} \left\| {\hat {P}x} \right\|=\left\| {\hat {P}x_{Ra} } \right\|. \end{align}

(25)

It can be easily verified that matrix $Q$ in (12) has the property $Q^{\rm T}Q=\left( {Q^{\rm T}Q} \right)^2$. This property enforces that $x^{\rm T}P^{\rm T}Px=x^{\rm T}\hat {P}^{\rm T}\hat {P}x$, for each $x\in {\bf R}^{Nd}$,and consequently $\left\| {Px} \right\|=\left\| {\hat {P}x} \right\|$. From this equality and (25),

\begin{align} \left\| {Px} \right\|=\left\| {\hat {P}x_{Ra} } \right\|. \end{align}

(26)

Since $T$ is an invertible matrix,the rank of matrix $Q^{\rm T}QT$ equals $N-1$. This means that matrix $Q^{\rm T}QT$ has one zero singular value (namely $\rho _1 =0$ ) and $N-1$ nonzero singular values denoted by $\rho _2 ,\rho _3 ,\ldots,\rho _N $. Hence,according to Lemma 4 the singular values of matrix $\hat {P}$ are

\begin{align} \underbrace {0,\ldots,0}_{d\mbox{ times}},\mbox{ }\underbrace {\rho _2 ,\ldots,\rho _2 }_{d\mbox{ times}},\underbrace {\rho _3 ,\ldots,\rho _3 }_{d\mbox{ times}},\ldots,\underbrace {\rho _N ,\ldots,\rho _N }_{d\mbox{ times}}. \end{align}

(27)

Now,consider the following two matrix inequalities

\begin{align} \left\| {Sx_{Ra} } \right\|\le \left\| S \right\|\left\| {x_{Ra} } \right\|, \end{align}

(28)

and

\begin{align} \rho _{\min } \left\| {x_{Ra} } \right\|\le \left\| {\hat {P}x_{Ra} } \right\|, \end{align}

(29)

for each $x_{Ra} \in Ra(\hat {P})=Ra(S)=Ra(P)$,where $\rho _{\min } $ indicates the minimum nonzero singular value of matrix $\hat {P}$. From (15) and (24),it is found that the only difference between matrices $Q^{\rm T}QT$ and $QT$ is an extra zero row. Hence,these two matrices have the same nonzero singular values (i.e. $\rho _2 ,\rho _3 ,\ldots,\rho _N )$. This means that $\rho _{\min } $ is the minimum singular value of matrix $QT$. According to (28) and (29),it is obtained that

\begin{align} \left\| {Sx_{Ra} } \right\|\le \left\| S \right\|\frac{\left\| {\hat {P}x_{Ra} } \right\|}{\rho _{\min } }. \end{align}

(30)

By substituting $\left\| {Sx_{Ra} } \right\|$ and $\left\| {\hat {P}x_{Ra} } \right\|$ respectively from (22) and (26) in (30),and noting that $\left\| S \right\|=N$ (Lemma 5),inequality (21) is deduced.

Finally,a geometric property for the region $\beta _\varepsilon ^\prime $ is revealed in the following lemma. Actually this lemma helps us to satisfy Constraint 2 in the controller design procedure of the next section.

Lemma 7. Define the set in Lemma 3 as $\bar {M}:= \{x\in {\bf R}^{Nd}\vert x_1 =x_2 =\cdots =x_N \}$. Also,assume that the positive constant $\varepsilon $ satisfies the condition

\begin{align} \varepsilon \le \mu ^2\rho _{\min } ^2, \end{align}

(31)

where $\mu \in {\bf R}^+$,$\rho _{\min } $ is the minimum singular value of matrix $QT$,$T$ is the transition matrix introduced in Section Ⅱ.-B and $Q$ is defined by (12). In this case $D(x,\bar {M})\le \mu $,$\forall x\in \beta _\varepsilon ^\prime =\{x\in {\bf R}^{Nd}\vert x^{\rm T}zx\le \varepsilon \}.$

Proof. Consider $\bar {m}=[\hat {m},\hat {m},\ldots,\hat {m}]^{\rm T}\in {\bf R}^{Nd}$ as a member of the set $\bar {M}$.

Then for each $x\in \beta _\varepsilon ^\prime $,$D(x,\bar {M})$ is defined as

\begin{align} &D(x,\bar {M})=\mathop {\inf }\limits_{\bar {m}\in \bar {M}} \mbox{ }\left\| {x-\bar {m}} \right\|\nonumber \\ & =\mathop {\inf }\limits_{\hat {m}\in {\bf R}^d} \mbox{ }\sqrt {\left\| {x_1 -\hat {m}} \right\|^2+\left\| {x_2 -\hat {m}} \right\|^2+\cdots+\left\| {x_N -\hat {m}} \right\|^2} \end{align}

(32)

By setting the gradient of $\left\| {x_1 -\hat {m}} \right\|^2+\left\| {x_2 -\hat {m}} \right\|^2+\ldots+\left\| {x_N -\hat {m}} \right\|^2$ with respect to $\hat {m}$ equal to zero, it is found that the minimum of this function occurs at $\hat {m}=\hat {m}^\ast $ where

\begin{align} \hat {m}^\ast =\frac{1}{N}\sum\limits_{i=1}^N {x_i } . \end{align}

(33)

Hence,the distance of $x$ from $\bar {M}$ is equal to $\left\| {x-\bar {m}^\ast } \right\|$ where $\bar {m}^\ast =[\hat {m}^\ast ,\hat {m}^\ast ,\ldots,\hat {m}^\ast]^{\rm T}$. Consequently, (34) is concluded.

$$D(x,\bar M) = {{\sqrt {{{\left\| {(N - 1){x_1} - {x_2} - \cdots - {x_N}} \right\|}^2} + \cdots + {{\left\| {(N - 1){x_N} - {x_1} - \cdots - {x_{N - 1}}} \right\|}^2}} } \over N}.$$

(34)

According to the definition of matrix $S$ in Lemma 5, (34) can be written as

\begin{align} D(x,\bar {M})=\frac{\left\| {Sx} \right\|}{N}. \end{align}

(35)

As we know,the set $\beta _\varepsilon ^\prime =\{x\in {\bf R}^{Nd}\vert x^{\rm T}zx\le \varepsilon \}$ indicates all the points placed inside the surface $x^{\rm T}zx=\varepsilon $. According to the definition of $z,$ i.e. $z=P^{\rm T}P$,we have

\begin{align} \left\| {Px} \right\|^2\le \varepsilon, \end{align}

(36)

for each $x$ in the set $\beta _\varepsilon ^\prime =\{x\in {\bf R}^{Nd}\vert x^{\rm T}zx\le \varepsilon \}$. Inequalities (31) and (36) result in

\begin{align} \left\| {Px} \right\|\le \mu \rho _{\min }. \end{align}

(37)

Finally,(21) and (37) yield in the following inequality for the distance indicated by (35).

\begin{align} D(x,\bar {M})=\frac{\left\| {Sx} \right\|}{N}\le \mu \end{align}

(38)

Ⅳ. Design of the Stabilizing Controller

In this section,the aim is to design a controller for the swarm system (1) such that asymptotic swarm stability is guaranteed and the Constraints 1 and 2 are simultaneously met. To this end,at first in Section Ⅳ-A two useful theorems from ^[36] have been restated. Then,the control law is proposed in Section Ⅳ-B.

A. Two Useful Theorems

At first,let us restate a theorem related to the asymptotic stability of fractional order linear time invariant systems subject to input saturation.

Theorem 1. ^[36] Consider the following fractional order linear time invariant system

\begin{align} D_t^\alpha x(t)=\bar {A}x(t)+\bar {B}sat(u(t)),\mbox{ }x(0)=x_0, \end{align}

(39)

where $0<\alpha <1$,$x(t)\in {\bf R}^n$ ,$u(t)\in {\bf R}^m, \bar {A}\in {\bf R}^{n\times n}_{,} \quad \bar {B}\in {\bf R}^{n\times m}_{ }$ and the saturation function $sat(u(t)):{\bf R}^m\to {\bf R}^m$ is of the form

\begin{align} sat(u(t))=[sat(u(t)_{(1)}),sat(u(t)_{(2)}),\ldots,sat(u(t)_{(m)} )]^{\rm T}, \end{align}

(40)

where $sat(u(t)_{(l)} ),l=1,2,\ldots,m$ is defined as follows.

\begin{align} sat(u(t)_{(l)} )={\rm sgn}(u(t)_{(l)} )\min (\bar {u}(t)_{(l)} ,\left| {u(t)_{(l)} } \right|). \end{align}

(41)

Also,assume that $u(t)=Kx(t),$ where $K\in {\bf R}^{m\times n}$. If there exists a diagonal matrix $\gamma ={\rm diag}\{\gamma _1 ,\gamma _2 ,\ldots,\gamma _m \}$ such that $0<\gamma _i \le 1$ for all $i=1,\ldots,m$ and $\left| {\arg (eig(\bar {A}+\bar {B}\gamma K))} \right|>\alpha \pi /2$,then there exists a sufficiently small closed ball, denoted by $\beta _\delta:= \{x\in {\bf R}^n\vert \left\| x \right\|\le \delta \}$,such that system (39) is asymptotically stable for any $x_0 \in \beta _\delta \subset S(\gamma K,u_0 )$,where ${u_o} = {[{u_{o{\rm{(1)}}}},{u_{o{\rm{(1)}}}}, \ldots ,{u_{o(m)}}]^{\rm{T}}}$ ,$u_{o(i)} \in {\bf R}^+_{ }$ denotes the saturation level for the $i$-th input ($i=1,\ldots,m)$,and $S(\gamma K,u_0 )$ is defined by

\begin{align} S(\gamma K,u_0 )=\{x(t)\in {\bf R}^n\vert -u_0 \le \gamma Kx(t)\le u_0 \}. \end{align}

(42)

As mentioned in ^[36],asymptotic stability of (39) means that for every $\varepsilon >0$,there exists $\delta >0$ such that for every initial condition $x_0 \in \beta _\delta =\{x_0 \in {\bf R}^n\vert \left\| {x_0 } \right\|\le \delta \}$ the solution $x(t,x_0 )$ remains in the closed ball $\beta _\varepsilon:= \{x\in {\bf R}^n\vert \left\| x \right\|\le \varepsilon \}$. In ^[36],it has been shown that the region $\beta _\varepsilon $,can be used to estimate $S(\gamma K,u_0 )$ in (42). Also,the following theorem has been proved which presents a procedure to determine the state feedback control gain $K$.

Theorem 2. ^[36] Consider system (39) with the state feedback controller $u(t)=Kx(t)$,$K\in {\bf R}^{m\times n}$. If there exists matrix $X\in {\bf R}^{m\times n}$,symmetric positive definite matrix $H\in {\bf R}^{n\times n}$,diagonal matrix $\gamma ={\rm diag}\{\gamma _1 ,\gamma _2 ,\ldots,\gamma _m \}$ ($0<\gamma _i \le 1$ for all $i=1,\ldots,m)$,and positive constant $\varepsilon $ such that

\begin{align} \sum\limits_{i=1}^2 {sym\{\Theta _{i1} \otimes (\bar {A}H+\bar {B}X)\}} <0, \end{align}

(43)

\begin{align} \sum\limits_{i=1}^2 {sym\{\Theta _{i1} \otimes (\bar {A}H+\bar {B}\gamma X)\}} <0, \end{align}

(44)

\begin{align} \left[{{\begin{array}{*{20}c} {2H-\varepsilon I} & {\gamma _i X_{(i)}^{\rm T} } \\ {\gamma _i X_{(i)} } & {u_{0(i)}^2 } \\ \end{array} }} \right]\ge 0, \end{align}

(45)

where

\begin{align} \Theta _{11} =\Theta _{21}^{\rm T} =\left[{{\begin{array}{*{20}c} {\sin (\frac{\alpha \pi }{2})} & {-\cos (\frac{\alpha \pi }{2})} \\ {\cos (\frac{\alpha \pi }{2})} & {\sin (\frac{\alpha \pi }{2})} \\ \end{array} }} \right] , \end{align}

(46)

then the fractional order system (39) is asymptotically stabilizable for any $x_0 \in \beta _\delta $ by using the state feedback controller $u(t)=Kx(t)$ with the state feedback control gain $K=XH^{-1}$. Also,the trajectory $x(t,x_0 )$ is placed in the closed ball $\beta _\varepsilon =\{x\in {\bf R}^n\vert \left\| x \right\|\le \varepsilon \}$.

B. Constraint Swarm Stabilization

In this subsection,a controller for swarm stabilization of fractional order linear time invariant swarm systems is proposed which simultaneously satisfies Constraints 1 and 2. Before presenting this control law,consider the following assumption that is necessary for designing the swarm stabilizing controller in this subsection. It is assumed that the swarm system (1) satisfies the following assumption.

Assumption 2. In the fractional order linear time invariant swarm system (1),all the pairs of matrices $(A-\lambda _i F,B)$ for all $i=2,\ldots,N$ are stabilizable,where $\lambda _2 ,\ldots,\lambda _N \in {\bf R}^+$ denote the nonzero eigenvalues of the Laplacian matrix $L$.

Now,the proposed swarm stabilizing controller is presented in the following theorem which simultaneously satisfies Constraints 1 and 2.

Theorem 3. Consider the fractional order linear time invariant swarm system (1) which satisfies Assumptions 1 and 2. Also,assume that the positive constant $\varepsilon $ satisfies condition (31). Let $U=[u_1^{\rm T} ,\ldots,u_N^{\rm T}]^{\rm T}$ be given by

\begin{align} U=(T^{-1}Q^{\rm T}\otimes I_m )sat(\hat {K}(QT\otimes I_d )x), \end{align}

(47)

where the matrix $\hat {K}=XH^{-1}\in {\bf R}^{(N-1)m\times (N-1)d}$ is chosen such that the following matrix inequalities

\begin{align} \sum\limits_{i=1}^2 {sym\{\Theta _{i1} \otimes (\hat {A}H+\hat {B}X)\}} <0, \end{align}

(48)

and

\begin{align} \left[{{\begin{array}{*{20}c} {2H-\varepsilon I} & {X_{(i)}^{\rm T} } \\ {X_{(i)} } & {u_{0(i)}^2 } \\ \end{array} }} \right]\ge 0, \end{align}

(49)

are satisfied for matrix $X\in {\bf R}^{(N-1)m\times (N-1)d}$ and symmetric positive definite matrix $H\in {\bf R}^{(N-1)d\times (N-1)d}$,and $u_{o\mbox{ }i(l)} =\bar {u}_{i(l)} /\left\| {T^{-1}} \right\|_\infty $,$i=1,2,\ldots,N,\mbox{ }l=1,2,\ldots,m$ where $u_{o\mbox{ }i(j)} \in {\bf R}^+$ denotes the saturation level for the saturation function used in (47) and $T$ is the transition matrix introduced in Section Ⅱ-B. In this case,there is a region $\beta _\delta ^\prime : = \{ {x_0} \in {{\bf{R}}^{Nd}}|x_0^{\rm{T}}z{x_0} \le \delta \} \subset \hat S(\hat K,\bar u)$ ($\delta >0)$ such that the aforementioned swarm system is asymptotically swarm stable for any $x_0 \in \beta _\delta ^\prime $,where $\bar u = {[{\bar u_{{\rm{(1)}}}},{\bar u_{{\rm{(2)}}}}, \ldots ,{\bar u_{{\rm{( N)}}}}]^{\rm{T}}}$ ,$\bar {u}_{(i)} =[\bar {u}_{i\mbox{ }(1)} ,\bar {u}_{i\mbox{ }(2)} ,\ldots,\bar {u}_{i\mbox{ }(m)} ]^{\rm T}$ ($i=1,2,\ldots N)$,and the region $\hat {S}(\hat {K},\bar {u})$ is defined by

\begin{align} & \hat {S}(\hat {K},\bar {u})= \nonumber\\ & \{x(t)\in {\bf R}^{Nd}\vert -\bar {u}\le \left\| {T^{-1}} \right\|_\infty \hat {K}(QT\otimes I_d )x(t)\le \bar {u}\}. \end{align}

(50)

Also,in such a case the Constraints 1 and 2 are simultaneously satisfied for all $x_0 \in \beta _\delta ^\prime $.

Proof. Consider the system

\begin{align} D_t^\alpha \hat {x}=\hat {A}\hat {x}+\hat {B}sat(\hat {U}), \end{align}

(51)

which is a fractional order linear time invariant system subject to input saturation. Also,assume that matrices $\hat {A}$ and $\hat {B}$ in system (51) are in the forms introduced in (8). According to Theorem 1,if there exists diagonal matrix $\gamma ={\rm diag}\{\gamma _1 ,\gamma _2 ,\ldots,\gamma _{(N-1)m} \}$ such that $0<\gamma _i \le 1$ for all $i=1,\ldots,(N-1)m$ and $\left| {{\rm arg} (eig(\hat {A}+\hat {B}\gamma \hat {K}))} \right|>\alpha \pi /2$ for some $\hat {K}\in {\bf R}^{(N-1)d\times (N-1)m}$,then by using $\hat {U}=\hat {K}\hat {x}$ the system in (51) is asymptotically stable for any $\hat {x}_0 \in \beta _\delta \subset S(\gamma \hat {K},u_o )$,where $u_o \in {\bf R}^{(N-1)m}_{ }$ denotes the saturation level vector for the control input and $S(\gamma \hat {K},u_0 )$ is defined as

\begin{align} S(\gamma \hat {K},u_0 )=\{\hat {x}(t)\in {\bf R}^{(N-1)m}\vert -u_0 \le \gamma \hat {K}\hat {x}(t)\le u_0 \}. \end{align}

(52)

Consider matrix $\gamma _{ }$ as an identity matrix,i.e. $\gamma =I_{(N-1)m\times (N-1)m} $. Hence,the condition $\left| {{\rm arg} (eig(\hat {A}+\hat {B}\gamma \hat {K}))} \right|>\alpha \pi /2_{ }$ can be written as

\begin{align} \left| {{\rm arg} (eig(\hat {A}+\hat {B}\hat {K}))} \right|>\alpha \frac{\pi }{2}. \end{align}

(53)

$\hat {K}$ can be found for satisfying condition (53) if the pair $(\hat {A},\hat {B})$ is stabilizable. According to the block diagonal form of matrices $\hat {A}$ and $\hat {B}$ (See (8)),the stabilizability of the pair $(\hat {A},\hat {B})$ is deduced from the stabilizability of the pair matrices $(A-\lambda _i F,B)$ for all $i=2,\ldots,N$. This means that if Assumption 2 holds,$\hat {K}_{ }$ can be found for satisfying condition (53). On the other hand,based on Theorem 2 and considering matrix $\gamma _{ }$ as an identity matrix,Equations (48) and (49) can be used to find $\hat {K}$ in order to guarantee the asymptotic stability of system (51). Asymptotic stability of this system results in $\mathop {\lim }_{t\to \infty } \hat {x}(t)=0$,which is equivalent to asymptotic swarm stability of system (1) provided that Assumption 1 holds (Lemma 1).

Now,we are faced with four problems that need to be answered for completing the proof. First,obtaining the control signal $U\in {\bf R}^{Nm}$ in the form (47) to guarantee asymptotic stability of swarm system (1) according to the above-described control signal $\hat {U}=\hat {K}\hat {x}\in {\bf R}^{(N-1)m}$. Second,finding the upper bound of input controls in (3) (i.e.,$\bar {u})$ according to the saturation level of the saturation function in (47) (i.e.,$u_o )$ in order to show that Constraint 1 is met by using control signal (47). Third,obtaining the region $\hat {S}(\hat {K},\bar {u})_{ }$ based on the region $S(\gamma \hat {K},u_0 )$,and fourth,finding the positive constant $\varepsilon $ such that Constraint 2 is satisfied. The latter problem has been answered in Lemma 7. According to this lemma,to achieve the Constraint 2 the positive constant $\varepsilon $ in the region $\beta _\varepsilon ^\prime $ should satisfy (31).

The other issues will be answered in the following parts:

1) Finding the control signal $U\in {\bf R}^{Nm}$: Note that $U=[u_1^{\rm T} ,\ldots,u_N^{\rm T}]^{\rm T}\in {\bf R}^{Nm}$, $\tilde {U}=[\tilde {u}_1^{\rm T} ,\tilde {u}_2^{\rm T} ,\ldots,\tilde {u}_N^{\rm T}]^{\rm T}\in {\bf R}^{Nm}_{ }$and $\hat {U}=[\tilde {u}_2^{\rm T} ,\tilde {u}_3^{\rm T} ,\ldots,\tilde {u}_N^{\rm T}]^{\rm T}\in {\bf R}^{(N-1)m}$. According to the relation $\tilde {U}=(T\otimes I_m )U$,we have

\begin{align} U=(T^{-1}\otimes I_m )\tilde {U}, \end{align}

(54)

where $\tilde {U}=[\tilde {u}_1^{\rm T} ,\hat {U}^{\rm T}]^{\rm T}$. Assuming $\hat {U}=\hat {K}\hat {x}$ and considering the saturation function on $\hat {U}$ results in

\begin{align} U=(T^{-1}\otimes I_m )\left[{{\begin{array}{*{20}c} {\tilde {u}_1 } \\ {sat(\hat {K}\hat {x})} \\ \end{array} }} \right]. \end{align}

(55)

Matrix $(T^{-1}\otimes I_m )$ is in the following

form ^{[16, 18]}

\begin{align} (T^{-1}\otimes I_m )=\left[{{\begin{array}{*{20}c} {\hat {t}_{11} I_m } & \cdots \\ {\hat {t}_{11} I_m } & \cdots \\ \vdots & \ddots \\ {\hat {t}_{11} I_m } & \cdots & \end{array} }} \right]. \end{align}

(56)

By substituting $\hat {x}$ from (11) and $(T^{-1}\otimes I_m )$ from (56) into (55),it is Obtained that

\begin{align} \begin{array}{l} U=\left[{{\begin{array}{*{20}c} {\hat {t}_{11} I_m } & \cdots \\ {\hat {t}_{11} I_m } & \cdots \\ \vdots & \ddots \\ {\hat {t}_{11} I_d } & \cdots \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {\tilde {u}_1 } \\ {sat(\hat {K}(QT\otimes I_d )x)} \\ \end{array} }} \right] \\ \mbox{ }=(1_N \otimes (\hat {t}_{11} \tilde {u}_1 ))+(T^{-1}Q^{\rm T}\otimes I_m )sat(\hat {K}(QT\otimes I_d )x), \end{array} \end{align}

(57)

where $1_N =[\underbrace {1,1,\ldots,1}_N]^{\rm T}\in {\bf R}^{N\times 1}$ and $\tilde {u}_1 \in {\bf R}^m$ is an arbitrary input vector. By considering $\tilde {u}_1 $ as a zero vector,the input control (47) is achieved which yields asymptotic swarm stability in swarm system (1).

2) Finding the upper bound of control signal i.e. $\bar {u}$: By substituting $\tilde {U}$ with $sat(\tilde {U})$ in (54) and defining $_{ }M=[m_{i,j}] := (T^{-1}\otimes I_m )\in {\bf R}^{Nm\times Nm}$,one can obtain (58).

$$\left[ {\matrix{ {\left[ {\matrix{ {{u_{1,1}}} \cr \vdots \cr {{u_{1,m}}} \cr } } \right]} \cr {\left[ {\matrix{ {{u_{2,1}}} \cr \vdots \cr {{u_{2,m}}} \cr } } \right]} \cr \vdots \cr {\left[ {\matrix{ {{u_{N,1}}} \cr \vdots \cr {{u_{N,m}}} \cr } } \right]} \cr } } \right] = \left[ {\matrix{ {{m_{1,1}}} & {{m_{1,2}}} & \cdots & {{m_{1,Nm}}} \cr {{m_{2,1}}} & \cdots & \cdots & {{m_{2,Nm}}} \cr \vdots & \vdots & \ddots & \vdots \cr {{m_{Nm,1}}} & {{m_{Nm,2}}} & \cdots & {{m_{Nm,Nm}}} \cr } } \right]\left[ {\matrix{ {} \cr {\left[ {\matrix{ {sat({{\tilde u}_{1,1}})} \cr \vdots \cr {sat({{\tilde u}_{1,m}})} \cr } } \right]} \cr {\left[ {\matrix{ {sat({{\tilde u}_{2,1}})} \cr \vdots \cr {sat({{\tilde u}_{2,m}})} \cr } } \right]} \cr \vdots \cr {\left[ {\matrix{ {sat({u_{N,1}})} \cr \vdots \cr {sat({u_{N,m}})} \cr } } \right]} \cr } } \right].$$

(58)

For simplicity,we redefine $U=[u_1^\ast ,u_2^\ast ,\ldots,u_{Nm}^\ast]^{\rm T}$ and $\tilde {U}=[\tilde {u}_1^\ast ,\tilde {u}_2^\ast ,\ldots,\tilde {u}_{Nm}^\ast]^{\rm T}$. Hence, (58) can be rewritten as (59).

$$\left[ {\matrix{ {u_1^ * } \cr {u_2^ * } \cr \vdots \cr {u_{Nm}^ * } \cr } } \right] = \left[ {\matrix{ {{m_{1,1}}} & {{m_{1,2}}} & \cdots & {{m_{1,Nm}}} \cr {{m_{2,1}}} & \cdots & \cdots & {{m_{2,Nm}}} \cr \vdots & \vdots & \ddots & \vdots \cr {{m_{Nm,1}}} & {{m_{Nm,2}}} & \cdots & {{m_{Nm,Nm}}} \cr } } \right]\left[ {\matrix{ {sat(\tilde u_1^ * )} \cr {sat(\tilde u_2^ * )} \cr \vdots \cr {sat(\tilde u_{Nm}^ * )} \cr } } \right].$$

(59)

From (59),

\begin{align} u_i^\ast =\sum\limits_{j=1}^{Nm} {m_{i,j} sat(\tilde {u}_j^\ast )} ,\mbox{ }i=1,2,\ldots,Nm. \end{align}

(60)

Hence,the upper bound of control input $u_i^\ast $ is obtained as follows.

\begin{align} \left| {u_i^\ast } \right|\le u_{o(i)} \sum\limits_{j=1}^{Nm} {m_{i,j} } \le u_{o(i)} \sum\limits_{j=1}^{Nm} {\left| {m_{i,j} } \right|} ,\mbox{ }i=1,2,\ldots,Nm. \end{align}

(61)

According to the definition of infinity matrix norm,we have

\begin{align} \left\| M \right\|_\infty =\mathop {\max }\limits_{i=1,2,\ldots,Nm} \sum\limits_{j=1}^{Nm} {\left| {m_{i,j} } \right|} \mbox{ }. \end{align}

(62)

Finally,(61) and (62) result in

\begin{align} \left| {u_i^\ast } \right|\le u_{o(i)} \left\| M \right\|_\infty \mbox{ }i=1,2,\ldots,Nm. \end{align}

(63)

Now,from the properties of infinity matrix norm,the matrix norm $\left\| M \right\|_\infty $ in (63) can be written as

\begin{align} \left\| M \right\|_\infty =\left\| {T^{-1}\otimes I_d } \right\|_\infty =\left\| {T^{-1}} \right\|_\infty. \end{align}

(64)

Hence,(63) is written as

\begin{align} \left| {u_i^\ast } \right|\le u_{o(i)} \left\| {T^{-1}} \right\|_\infty,\mbox{ }i=1,2,\ldots,Nm. \end{align}

(65)

Choosing $u_{o(i)} \mbox{ },\mbox{ }i=1,2,\ldots,Nm$ as

\begin{align} u_{o(i)} =\frac{\bar {u}_i }{\left\| {T^{-1}} \right\|_\infty } \end{align}

(66)

results in the following saturation level as the upper bound for the $i$-th control input of input vector $U$ in (47).

\begin{align} \left| {u_i^\ast } \right|\le \bar {u}_i,\,i=1,2,\ldots,Nm. \end{align}

(67)

Consequently, if $\bar {u}_{i(l)} =\left\| {T^{-1}} \right\|_\infty u_{o\mbox{ }i(l)} \in {\bf R}^+$, $i=1,2,\ldots,N$,$l=1,2,\ldots,m $ Constraint 1 is satisfied by using control signal (47).

3) Obtaining the region $\hat {S}(\hat {K},\bar {u})$: According to (66),

\begin{align} u_o =\frac{\bar {u}}{\left\| {T^{-1}} \right\|_\infty }, \end{align}

(68)

where $u_o \in {\bf R}^{(N-1)m}_{ }$ and $\bar {u}\in {\bf R}^{Nm}$. By substituting (11) and (68) into (52) and considering the assumption $\gamma =I_{(N-1)m\times (N-1)m} $,the region $\hat {S}(\hat {K},\bar {u})$ in (48) is obtained.

Ⅴ. Numerical Simulations

In this section,the results of the previous section are verified by two numerical examples. Numerical simulations of this section have been done by using the Adams-type predictor-corrector method introduced in ^[43] for solving fractional order differential equations.

Example 1. Consider the following fractional order linear time invariant swarm system:

\begin{align} &D_t^{0.8} x_i =Ax_i +F\sum\limits_{j=1}^5 {w_{ij} (x_j -x_i )+B} u_i ,\nonumber \\&~~~~~~~~~~~~~~~~~~i=1,\ldots,5,\mbox{ } \end{align}

(69)

where

$$A = \left[ {\matrix{ {1.6} & { - 0.9} \cr 3 & {1.2} \cr } } \right],{\rm{ }}F = \left[ {\matrix{ {3.2} & { - 3} \cr 4 & 5 \cr } } \right],{\rm{ }}B = \left[ {\matrix{ 1 \cr 0 \cr } } \right].$$

(70)

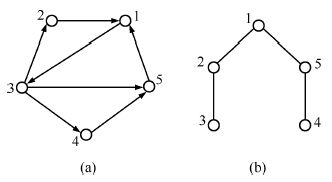
Graph $G_a $ expressing the communication among these agents is shown in Fig. 1(a). Also,the adjacency matrix of this graph is considered as

\begin{align*} W_{G_a } =\left[{{\begin{array}{*{20}c} 0 & {0.4} & 0 & 0 & {0.7} \\ 0 & 0 & {0.2} & 0 & 0 \\ {0.3} & 0 & 0 & 0 & 0 \\ 0 & 0 & {0.6} & 0 & 0 \\ 0 & 0 & {1.2} & {0.8} & 0 \\ \end{array} }} \right]. \end{align*}

In this case,the eigenvalues of the Laplacian matrix for the mentioned graph are $\lambda (G_a )=\{0,\mbox{ 0.2776,0.8856, 1.1811,1.8557}\}$. According to (8),matrices $\hat {A}_{ }$ and $\hat {B}$ are in the following forms:

$$\hat A = \left[ {\matrix{ {A - {\lambda _2}F} & 0 & 0 & \cdots & 0 \cr 0 & {A - {\lambda _3}F} & 0 & \cdots & 0 \cr 0 & \vdots & \vdots & \ddots & \vdots \cr \vdots & 0 & \cdots & \cdots & 0 \cr 0 & 0 & \cdots & 0 & {A - {\lambda _5}F} \cr } } \right] \in {{\bf{R}}^{8 \times 8}}$$

where

\begin{align*} A-\lambda _2 F&=\left[{{\begin{array}{*{20}c} {\mbox{0.7118}} & {-\mbox{0.0673}} \\ {\mbox{1.8897}} & {-\mbox{0.187}} \\ \end{array} }} \right], \\ A-\lambda _3 F\nonumber&=\left[{{\begin{array}{*{20}c} {-\mbox{1.2341}} & {\mbox{1.7569}} \\ {-\mbox{0.5426}} & {-\mbox{3.2282}} \\ \end{array} }} \right], \end{align*} \begin{align*} A-\lambda _4 F&=\left[{{\begin{array}{*{20}c} {-\mbox{2.1794}} & {\mbox{2.6432}} \\ {-\mbox{1.7243}} & {-\mbox{4.7053}} \\ \end{array} }} \right], \\ A-\lambda _5 F\nonumber&=\left[{{\begin{array}{*{20}c} {-\mbox{4.3383}} & {\mbox{4.6671}} \\ {-\mbox{4.4228}} & {-\mbox{8.0786}} \\ \end{array} }} \right], \end{align*}

and

\begin{align*} \hat {B}=\left[{{\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{array} }} \right]^{\rm T}. \end{align*}

It is worth noting that matrix $\hat {A}$ is not $\alpha $-Hurwitz with $\alpha =0.8$. In this example,the aim is asymptotic swarm stabilization of the above-described swarm system in the presence of Constraint 1 with saturation level $\bar {u}=[2;2;2;2;2]^{\rm T}$ and Constraint 2 with $\mu =1.8$. To achieve this aim,from Theorem 3 the control can be chosen as

\begin{align} U=(T^{-1}Q^{\rm T}\otimes I_1 )sat(\hat {K}(QT\otimes I_2 )x), \end{align}

(71)

where the matrices $T$ and $Q$ have the following forms:

$$\eqalign{ & T = \left[ {\matrix{ {{\rm{0}}{\rm{.2988}}} & {{\rm{0}}{\rm{.5976}}} & {{\rm{1}}{\rm{.0956}}} & {{\rm{0}}{\rm{.1394}}} & {{\rm{0}}{\rm{.1046}}} \cr {{\rm{0}}{\rm{.1977 }}} & { - {\rm{1}}{\rm{.0194}}} & {{\rm{0}}{\rm{.5420 }}} & {{\rm{0}}{\rm{.1994}}} & {{\rm{0}}{\rm{.0803}}} \cr { - {\rm{1}}{\rm{.3072}}} & {{\rm{0}}{\rm{.7626}}} & { - {\rm{0}}{\rm{.9340}}} & {{\rm{2}}{\rm{.2997}}} & { - {\rm{0}}{\rm{.8211}}} \cr {{\rm{2}}{\rm{.1783}}} & { - {\rm{0}}{\rm{.8881}}} & { - {\rm{0}}{\rm{.5886}}} & { - {\rm{2}}{\rm{.5635}}} & {{\rm{1}}{\rm{.8620}}} \cr {{\rm{ 0}}{\rm{.3645}}} & { - {\rm{0}}{\rm{.0881}}} & { - {\rm{0}}{\rm{.9182}}} & { - {\rm{1}}{\rm{.1266}}} & {{\rm{1}}{\rm{.7683}}} \cr } } \right], \cr & Q = {\left[ {\matrix{ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \cr 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \cr } } \right]_{4 \times 5}}. \cr} $$

Considering $\left\| {T^{-1}} \right\|_\infty =2.657$,the saturation level is chosen as $u_0 =\mbox{ 0.7527}$ (See (68)). Moreover since $\mu =1.8$ and $\rho _{\min } =0.6819$,one can choose $\varepsilon =1.5$ to satisfy (31). Solving the matrix inequalities in (48) and (49) with $\varepsilon =1.5$ results in the matrix $\hat {K}$ as follows.

\begin{align} \hat {K}=[\hat {K}_1 \mbox{ }\hat {K}_2]\in {\bf R}^{4\times 8}, \end{align}

(72)

where

$$\eqalign{ & {{\hat K}_1} = \left[ {\matrix{ { - {\rm{7}}{\rm{.6211}}} & { - {\rm{2}}{\rm{.6937}}} & 0 & 0 \cr 0 & 0 & { - {\rm{1}}{\rm{.1352}}} & { - {\rm{1}}{\rm{.2980}}} \cr 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 \cr } } \right] \in {{\bf{R}}^{4 \times 4}} \cr & {{\hat K}_2} = \left[ {\matrix{ {0\;} & 0 & 0 & 0 \cr 0 & 0 & 0 & {\rm{0}} \cr { - {\rm{1}}{\rm{.1076}}} & { - {\rm{2}}{\rm{.2546}}} & 0 & 0 \cr 0 & 0 & { - {\rm{2}}{\rm{.3234}}} & { - {\rm{4}}{\rm{.5966}}} \cr } } \right] \in {{\bf{R}}^{4 \times 4}} \cr} $$

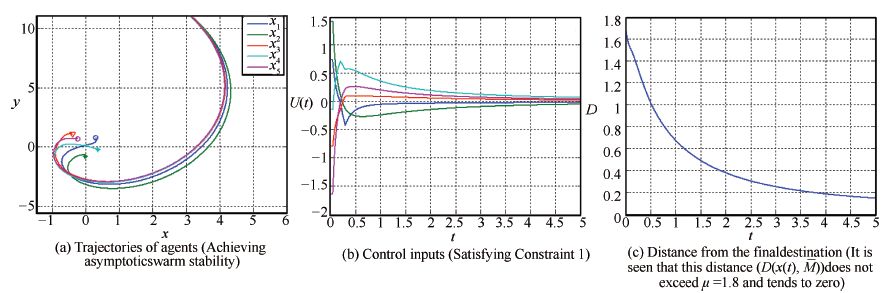
As shown in Fig. 2,the considered aim is achieved by applying the control law (71). More precisely,Fig. 2(a) confirms that asymptotic swarm stability is achieved. Also,Figs. 2(b) and 2(c) respectively reveal that Constraint 1 with saturation level $\bar {u}=[2;2;2;2;2]^{\rm T}$ and Constraint 2 with $\mu =1.8$ are satisfied.

Example 2. Consider the following fractional order linear time invariant swarm system with five agents

\begin{align} D_t^{0.8} x_i =Ax_i +F\sum\limits_{j=1}^5 {w_{ij} (x_j -x_i )+B} u_i \mbox{ },\mbox{ }i=1,\ldots,5.\mbox{ } \end{align}

(73)

\begin{align} A=\left[{{\begin{array}{*{20}c} {-0.1} & {0.7} \\ {-5.2} & {1.8} \\ \end{array} }} \right],\mbox{ }F=\left[{{\begin{array}{*{20}c} 2 & {-10} \\ 4 & {-6} \\ \end{array} }} \right],\mbox{ }B=\left[{{\begin{array}{*{20}c} 2 & 0 \\ 0 & 1 \\ \end{array} }} \right]. \end{align}

(74)

The undirected graph $G_b $ describing the communication among these agents is shown in Fig. 1(b). Also,the adjacency matrix of this graph is considered as

\[ W_{G_b } =\left[{{\begin{array}{*{20}c} 0 & {1.2} & 0 & 0 & {0.8} \\ {1.2} & 0 & {0.4} & 0 & 0 \\ 0 & {0.4} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {0.9} \\ {0.8} & 0 & 0 & {0.9} & 0 \\ \end{array} }} \right]. \]

The eigenvalues of the Laplacian matrix for the mentioned graph are as follows:

\[ \lambda (G_b )=\{0,\mbox{ 0.2935,0.8222,2.1424,3.3419}\} \]

The matrices $\hat {A}_{ }$ and $\hat {B}$ in this example are

\[ \hat {A}=\left[\!\! {{\begin{array}{*{20}c} {A-\lambda _2 F} & 0 & 0 & \cdots & 0 \\ 0 & {A-\lambda _3 F} & 0 & \cdots & 0 \\ 0 & \vdots & \vdots & \ddots & \vdots \\ \vdots & 0 & \cdots & \cdots & 0 \\ 0 & 0 & \cdots & 0 & {A-\lambda _5 F} \\ \end{array} }} \!\!\right]\in {\bf R}^{8\times 8} \]

where

$$\eqalign{ & A - {\lambda _2}F = \left[ {\matrix{ { - 0.6871} & {3.6354} \cr { - 6.3742} & {3.5613} \cr } } \right], \cr & A - {\lambda _3}F = \left[ {\matrix{ { - 1.7444} & {8.9222} \cr { - 8.4889} & {6.7333} \cr } } \right], \cr} $$

\[ A-\lambda _4 F =\left[{{\begin{array}{*{20}c} {-4.3848} & {22.1239} \\ {-13.7695} & {14.6543} \\ \end{array} }} \right],\]

\[A-\lambda _5 F =\left[{{\begin{array}{*{20}c} {-6.7837} & {34.1185} \\ {-18.5674} & {21.8511} \\ \end{array} }} \right], \]

and

\[ \hat {B}={\rm diag}\{2,1,2,1,2,1,2,1\}.\]

Matrix $\hat {A}$ is not $\alpha $-Hurwitz with $\alpha =0.8$. In this case,matrices $T$ and $Q$ have the following forms:

\[ \begin{array}{l} T=\left[{{\begin{array}{*{20}c} {-0.447} & {-0.447} & {-0.447} & {-0.447} & {-0.447} \\ {-0.032} & {0.196} & {0.736} & {-0.537} & {-0.362} \\ {0.501} & {0.519} & {-0.492} & {-0.486} & {-0.042} \\ {0.181} & {-0.481} & {0.110} & {-0.499} & {0.689} \\ {-0.718} & {0.511} & {-0.069} & {-0.162} & {0.439} \\ \end{array} }} \right] \\ \qquad \qquad Q=\left[{{\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} }} \right]_{4\times 5} \\ \end{array} \]

Suppose that all the input control signals are subjected to constraint with upper bound 4,i.e. $\bar {u}=[4;4;4;4;4;4;4;4;4;4]^{\rm T}$ in Constraint 1. Moreover,the aim is to achieve asymptotic swarm stability in the considered swam system while Constraint 2 with $\mu =1.5$ is satisfied. To achieve asymptotic swarm stability with considering the mentioned constraints,according to Theorem 3 the control law is chosen in the following form

\begin{align} U=(T^{-1}Q^{\rm T}\otimes I_2 )sat(\hat {K}(QT\otimes I_2 )x). \end{align}

(75)

From equality $\left\| {T^{-1}} \right\|_\infty =2.1538$,the saturation level is obtained as $u_0 =1.8572$. Also since $\rho _{\min } =1$,we choose $\varepsilon =1$ to satisfy (31). Solving the matrix inequalities (48) and (49) with $\varepsilon =1$ yields

\begin{align} \hat {K}={\rm diag}\{\hat {K}_1 ,\hat {K}_2 ,\hat {K}_3 ,\hat {K}_4 \}\in {\bf R}^{8\times 8}, \end{align}

(76)

where

\[\hat {K}_1 =\left[\!\! {{\begin{array}{*{20}c} {-4.8508} & {2.3989} \\ {6.8251} & {-7.6845} \\ \end{array} }} \!\!\right],\\ \hat {K}_2 =\left[\!\! {{\begin{array}{*{20}c} {-5.6536} & {2.2859} \\ {9.8021} & {-16.0606} \\ \end{array} }} \!\!\right], \] \[ \hat {K}_3 =\left[\!\! {{\begin{array}{*{20}c} {-9.2684} & {5.0800} \\ {19.4285} & {-44.1909} \\ \end{array} }}\!\! \right],\\ \hat {K}_4 =\left[\!\! {{\begin{array}{*{20}c} {-16.9353} & {21.5528} \\ {41.1281} & {-108.9224} \\ \end{array} }} \!\!\right]. \]

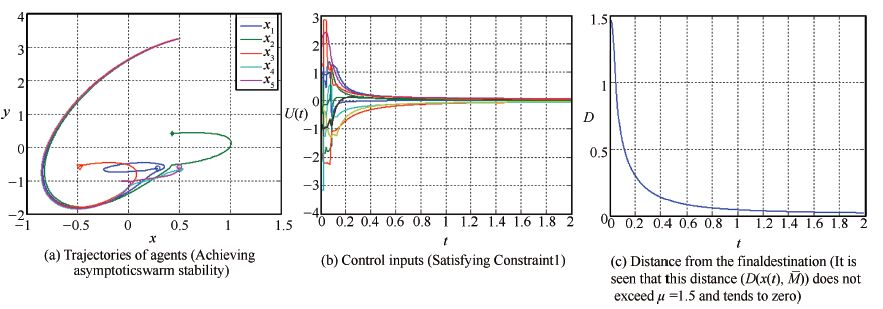
Numerical simulation results presented in Fig. 3(a) confirm that asymptotic swarm stability is achieved by applying the control law (75) with the obtained specifications. Moreover, Figs. 3(a) and 3(c) verify that the aforementioned constraints are also satisfied in this case. For a comparison,simulation results of the swarm system in (73) by applying control law (75) and without considering saturation function in this law (unsaturated control inputs) have been presented in Fig. 4. By comparing the simulation results of Figs. 3 and Fig. 4,it can be seen that without considering the input constraint,the convergence rate of the agents to reach consensus increases. But in this case,as a negative point the values of control inputs at the beginning of the motion are too large which can cause practical problems due to physical constraints of the actuators in the real-world applications. This means that involving Constraint 1 in design procedure can yield in more applicable control signals.

As it is confirmed by the above-mentioned numerical examples,by using the feedback control law (47) asymptotic swarm stability is achieved in fractional order linear time invariant swarm system (1) with a directed/undirected topology graph satisfying Assumption 1. Applying this control law,the distance of the agents from the final destination is less than a desired value. In addition,the input signals do not exceed a predetermined value.

Ⅵ. Conclusion

Constrained swarm stabilization of fractional order linear time invariant swarm systems is studied in this paper. In this study,a bounded state-feedback control law is proposed to ensure asymptotic swarm stability in fractional order swarm systems. This law enforces that the distance of agents from the final destination is less than a desired value. Numerical simulation results demonstrated the effectiveness of the proposed control law.