2. Department of Automation, Shanghai JiaoTong University, and also with the Key Laboratory of System Control and Information Processing, Ministry of Education of China, Shanghai 200240, China
IN this paper,we focus on the domain of attraction of the original for a class of fractional order systems with saturating actuators. Fractional order systems,which are based on fractional calculus,have attracted much attentions in recent decades. Fractional calculus has a long history over 300 years,and it is a branch of mathematical analysis that deals with the possibility of taking real number or complex number powers of differentiation and integration operators [1] . In recent years,considerable interest in fractional calculus has been stimulated by the applications that this calculus found in numerical analysis and different areas of physics and engineering,possibly including fractal phenomena [2] . Especially in some special areas,such as viscoelastic materials [3] and electro-chemical systems [4] ,the application of fractional-order models is more adequate and elegant than integer-order models for the investigation of dynamic behavior. The most significant reason is that the fractional differential equations (FDEs) have the ability of revealing inherent memory and inherited character of various materials and processes in real physical world.
In control engineering field,the fractional order $PI^\lambda D^\mu$ (FOPID) controller is an active topic for its excellent control performance and the tuning method for FOPID controller has attract more attentions. In the past decades,a number of tuning methods for fractional order controllers are proposed in the literatures,such as [5, 6, 7]. However,most of obtained results are derived in the frequency domain,and it is hard to handle nonlinearities,e.g.,actuator saturation,of the considered systems.
The stability and stabilization problems of integer order state space model have been widely investigated. In [8], a method for estimating the domain of attraction of the origin for a system under a saturated linear feedback is proposed. And in [9], the stability and stabilization problems of a class of continuous-time and discrete-time Markovian jump linear systems with partly unknown transition probabilities are investigated. The robust stochastic stability problem for discrete-time uncertain singular Markov jump systems with actuator saturation is considered in [10]. As the extension of integer order systems,the stability and stabilization problems of fractional order state space model also have attracted great attractions. Control problems of fractional order systems have achieved tremendous attention in recent years due to the inherent memory advantage of fractional derivatives.
Iterative learning control is one of important robust linear control methods for fractional order linear systems. In [11], Chen investigated the classical Arimoto D-type iterative learning control (ILC) updating law uses the first order derivative (with transfer functions) of tracking error. The convergence of the iterative process for fractional order linear systems was first discussed in time domain in [12], which is a meaningful work,and the fractional order iterative learning control for time-varying systems in convolution form are analyzed. In [13], Li discussed the convergence of the iterative process for fractional order linear time invariant (LTI) system,and proved that the convergence conditions of the fractional order and integer order iterative learning schemes are equivalent for $D=0$.
Another important issue is the robust stability and stabilization problems of fractional order systems. In [14], the problems of robust stability and stabilization for a class of fractional order linear time invariant systems with convex polytopic uncertainties were considered. Several methods to investigate the stability and stabilization of fractional order linear systems are proposed in [15] and [16] which are based on the conclusion in [14]. In this years,the control synthesis of fractional order system was wide investigated. Reference [17] investigated the robust stability of uncertain parameters FO-LTI interval systems,which have deterministic linear coupling relationship between fractional order and other model parameters. The robust stability for uncertain fractional-order systems of two types of order $\alpha \in (0,1)$ are investigated in [18].
In engineering practice,it is important to consider the input saturation. The performance of the closed-loop system may be severely degraded or be unstable when the actuator is under saturation. The actuator saturation for the integer order systems has received great attention in the past decades. However,in the stability analysis of fractional order systems,it is still an open topic. In this paper,we consider the control of fractional order linear systems subject to actuator saturation ${D}^\alpha x(t) = Ax(t)+BSat(u(t))$. To ensure the stabilization of this fractional order linear system,we first concern with the closed-loop stability under a given linear state feedback $u=Fx$. The Lyapunov approach is the mostly fundamental approach to deal with the stability issues of integer order systems. However,it is still an open topic to choose proper Lyapunov function candidates for fractional order systems. Several works have been dedicated to this problem.
For stable fractional order systems,the decay rate of solution is in the sense of Mittag-Leffler function rather than exponential function,which motivates the concept of Mittag-Leffler stability of fractional order systems. Mittag-Leffler stabilities were firstly proposed in [19] and [20] for the commensurate case and incommensurate case,respectively. Even though the generalization of classical Lyapunov direct approach to the fractional order case is proposed,the commonly used quadratic Lyapunov function candidate is not valid for fractional order systems since the fractional derivative of composite function is an infinite series. To the best of our knowledge,stability analysis of fractional order systems based on the Lyapunov direct approach is still an open problem,and only a few works are dedicated to this topic. By the equivalent transformation between the solution of FDEs with that of ODEs,the Lyapunov direct approach was adopted to investigate the stability of fractional order nonlinear systems [21] .
Only few works are related to the estimation of domain of attraction for fractional order systems. Such as,in [22], the sector bounded condition of saturation nonlinearity and Gronwall-Bellman inequality were adopted to derive estimation algorithm of attraction in terms of bilinear matrix inequality.
Our contributions of this paper include:
1) Propose a method to obtain the domain of attraction for fractional order systems through a set of ellipsoids.
2) Demonstrate that the convex hull of ellipsoids can be made invariant for fractional order linear systems subject to actuator saturation if each ellipsoid in a set with a bounded control of the saturating actuators is invariant.
By comparing our paper with the previous conclusions,it could be observed that less conservative results were obtained through the proposed method.
The rest of this paper is organized as follows: In Section Ⅱ,some necessary preliminaries and the problem statement are introduced. The domain of attraction under a given saturated linear feedback is discussed in Section Ⅲ. To obtain the feedback matrix,the construction of continuous feedback laws are introduced in Section Ⅳ. To show the effectiveness of this method,two numerical examples are shown in Section V. Finally,Section Ⅵ draws the conclusion.
Notations. ${\bf R}^n$ is the set of real $n$ dimensional vectors,and $\textbf{R}^{n \times m}$ is the set of real $n \times m$ dimensional matrices. $Sat(\cdot)$ stands for the standard saturation function. For a $P \in \textbf{R}^{n \times n}$,$P > 0$ and $\rho \in (0 ,\infty)$,an ellipsoid is denoted as $\Psi(P,\rho):=\{x \in \textbf{R}^n: x^{\rm T}Px \le \rho\}$ where $P$ is a positive-definite matrix. Especially,we use $\Psi(P)$ to denote $\Psi(P,1)$. In this paper,we are interested in a convex function determined by a set of positive-definite matrices ${P_1},{P_2},{P_3}, \ldots $, ${P_N} \in {{\bf{R}}^{n \times n}}$ to obtain the maximum estimation on the invariance of the considered fractional order systems.
Ⅱ. Problem Statement and Necessary Preliminaries A. Preliminaries
Definition 1. [23] A quadratic function can be defined as follows:
$$V_c(x)=x^{\rm T}Px,$$
$$L_{V_c}(\rho):=\{x \in \textbf{R}^n; V_c(x) \le \rho \}=\Psi(P,\rho).$$
\begin{equation*}
\mathcal{I}{^\alpha}f(t)=D^{-\alpha}f(t)=\frac{1}{\Gamma(\alpha)}
{\int_0^t\frac{f(\tau)}{(t-\tau)^{1-\alpha}}{\rm d}\tau}.
\end{equation*}
\begin{equation*}
{D}^{\alpha}f(t)=\frac{1}{\Gamma(m-\alpha)}{\int_0^t\frac{f^{(m)}(\tau)}
{(t-\tau)^{1+\alpha-m}}{\rm d}\tau},
\end{equation*}
Lemma 1 [23] For a set of positive-definite matrices
$P_1,P_2,P_3,\ldots,P_N \in {\bf R}^{n \times n}$,Let
$P(\gamma):=\sum_{j=1}^N\gamma_jP_j$,Then,
$$L_{V_c}(\rho)=co\{\Psi(P_j,\rho),j \in I[1,N]\} = \bigcup_{\gamma \in \Gamma}\Psi(P(\gamma),\rho),$$
Lemma 2 [24] Let $x(t) \in \textbf{R}^n$ be a vector of differentiable functions. Then,for any time instant $t \ge 0$,the following relationship holds
\begin{equation*}
D^{\beta}(x^{\rm T}(t)Px(t)) \le 2x^{\rm T}(t)P(D^{\beta}x(t)),
\end{equation*}
Lemma 3 [25] Define $\Phi(F) = \{ x\in \textbf{R}^{n}: |f_i x|\le1,i\in[1,m]\}$ ,and $f_i$ is the $i$-th row of the matrix $F$. Let $P \in \textbf{R}^{n \times n}$ be a positive-definite matrix. Suppose that $\rho>0$. An ellipsoid $\Omega(P,\rho) = \{x\in \textbf{R}^{n}: x^{\rm T}Px\le \rho\}$ is included in $\Phi(F)$ if and only if,
| \begin{equation*} {f_i^{\rm T}}Pf_i\le\rho. \end{equation*} |
Let $\varXi$ denote the set of $m \times m$ diagonal matrices whose diagonal elements are either $0$ or $1$. Then,there are $2^m$ elements in $\varXi$. Suppose that elements of $\varXi$ are labeled as $E_i$ with $i \in [1,2^m]$. Then,$E_i^{-} = I_m - E_i$ is also an element of $\varXi$,where $I_m$ is the $m \times m$ dimensional identity matrix.
Lemma 4 [25] Given $F,H\in \textbf{R}^{m \times n}$. Suppose that $\mid h_j x \mid \le 1$,then we have
\begin{equation*}
Sat(Fx) \in co \{ E_i Fx + E_i^{-}Hx,i\in[1,2^m]\},
\end{equation*}
Lemma 5 [19] Let $x=0$ be an equilibrium point for the non-autonomous fractional order system $D^\alpha x(t) = f(t,x)$. Assume that there exists a Lyapunov functin $V(t,x)$ and three class-$K$ functions $\beta_i,i=1,2,3$ satisfying
\begin{equation*}
\beta_1(\|x\|) \le V(t,x) \le \beta_2(\|x\|),
\end{equation*}
\begin{equation*}
D^{\beta}V(t,x) \le - \beta_3(\|x\|),
\end{equation*}
Lemma 6 [26] Considering an ellipsoid $\Psi(P)$,if
there exists an $H \in {\bf R}^{m \times n}$ such that
\begin{equation*}
\begin{split}
&(A+BE_iF+E_i^{-}H)^{\rm T}P+P(A+BE_iF\\
&\qquad+E_i^{-}H)<0,\forall i \in I[1,2^m],
\end{split}
\end{equation*}
Considering the open-loop fractional order linear system subject to actuator saturation:
\begin{equation}\label{satsystem}
D^\alpha x(t) = Ax(t) + BSat(u),
\end{equation}
(1)
The objective of this paper is to obtain an estimation of the domain of attraction for system (1) and obtain a feedback law $u=Sat(Fx)$,under which the closed-loop system,
\begin{equation}\label{satsystemfeedback}
D^\alpha x(t) = Ax(t) + BSat(Fx),
\end{equation}
(2)
Remark 1. Lyapunov stability method is an important tool for stability analysis of nonlinear systems. There are two methods to explore the stability of nonlinear systems: the Lyapunov indirect approach and the Lyapunov direct approach. In previous work [27], we utilized the Lyapunov indirect approach and Gronwall-Bellman inequality to analyse the decay law of solution. It is an effective way to investigate the global asymptotic stability and controller synthesis of fractional order systems with nonlinearity. However,we are interested in the invariance of considered systems in this study,which means we are more concerned about the local asymptotic stability than the global asymptotic stability. Therefore,the method in [27] is not enough to handle the invariance estimation problem of fractional order systems with actuator saturation.
The Lyapunov direct approach introduce an energy function to analysis the stability of the nonlinear system directly. It is an efficient way to investigate the invariance of nonlinear system. In this paper,we primarily consider Mittag-Leffler stability of the closed-loop systems with the state feedback law using Lyapunov direct approach.
Remark 2. From Definition 1 and [18], one can obtain that the quadratic function $V_c(x)=x^{\rm T}Px$ is the most popular Lyapunov function candidate to investigate the stability and control method of integer order systems. However,for fractional order systems,it is not suitable to use this function directly. The main reason for this problem is that the quadratic Lyapunov function is not valid since the fractional derivative of composite function is an infinite series. Lemma 2 provides a direct way to adopt this quadratic Lyapunov function for the fractional order systems. Thus the quadratic Lyapunov function can be used to analyze the stability and stabilization of fractional order system by expressing a linear feedback law subject to saturation into a convex hull of a group of auxiliary linear feedback matrices.
The objective of this paper is to obtain a series of feedback
functions to reduce the conservatism of the domain of attraction. To
that end,we are interested in a function determined by a set of
positive-definite matrices $P_1,P_2,P_3,ldots,P_N \in
\textbf{R}^{n \times n}$. Let $Q_j=P_j^{-1}$,$j \in I[1,N]$. For a
vector $\gamma \in \textbf{R}^N$, define
$$Q(\gamma):=\sum_{j=1}^N\gamma_jQ_j,\qquad P(\gamma):=Q^{-1}(\gamma),$$
$$V_c(x)=x^{\rm T}P(\gamma)x.$$
In this section,we consider the calculation problems corresponding to the quadratic function and apply it to fractional order linear systems. And then the estimation of the domain of attraction is illustrated.
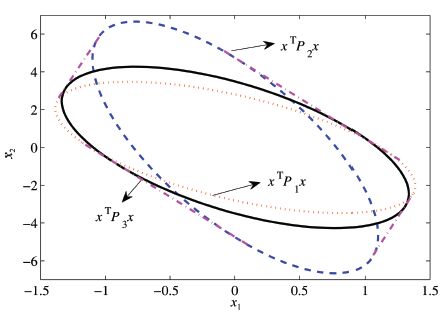
A. Calculation ProblemsFrom [26] and Remark 2,we know different reference polyhedrons will result in different ellipsoid set. Obviously,a single ellipsoid will result in much conservation. To deal with this situation and reduce the conservatism of the estimation,in this paper,a set of reference polyhedrons is used to produce multiple ellipsoids. Thus,these ellipsoids will combined to a convex hull and it can extend the domain of the invariant set $\Psi(P,\rho)$. One convex hull which is combined by three ellipsoids is shown in Fig. 1. We denote the convex hull of the ellipsoids
| \begin{equation*} \begin{split} co\{\Psi(P_j,\rho),&j \in I[1,N]\\&:=\{\displaystyle{\sum_{j=1}^N}\gamma_jx_j: x_j \in \Psi(P_j,\rho),\gamma \in \Gamma\}. \end{split} \end{equation*} |
|
Download:
|
| Fig. 1 The invariant set which is the convex hull of three ellipsoids. (See the magenta dash-dotted outer curve. | |
There are various ways to define the composite quadratic function
with a set of matrices $P_1,P_2,\,\ldots,\,P_N > 0$. For the
convenience of analysis,we define this function as follows,
$$V_c(x):= \max_{\gamma \in \Gamma} x^{\rm T}\left(\sum_{j=1}^N\gamma_j P_j\right)x,\quad \sum_{j=1}^N\gamma_j=1.$$
$$\eqalign{
& {V_c}(x) = {\max _{\gamma \in \Gamma }}{x^{\rm{T}}}\left( {\sum\limits_{j = 1}^N {{\gamma _j}} {P_j}} \right)x \cr
& = \mathop {\max }\limits_{\lambda { \in ^{[0,1]}}} {x^T}{\left( {\lambda {Q_1} + (1 - \lambda )){Q_2}} \right)^{ - 1}}x, \cr} $$
(3)
$$\mathop {\sup }\limits_{\gamma \in \Gamma } \delta ,$$
(4)
$$\eqalign{
& {\rm{s}}{\rm{.t}}{\rm{.}}\left[ {\matrix{
\delta & {{x^{\rm{T}}}} \cr
x & {\mathop \sum \limits_{j = 1}^N {\gamma _j}{Q_j}} \cr
} } \right] \ge 0,\sum\limits_{j = 1}^N {{\gamma _j}} = 1, \cr
& \Rightarrow {\rm{s}}{\rm{.t}}{\rm{.}}\left[ {\matrix{
\delta & {x_i^{\rm{T}}} \cr
{{x_i}} & {{\rm{ }}\lambda {Q_1} + (1 - \lambda ){Q_2}} \cr
} } \right] \ge 0. \cr} $$
(5)
Fig. 1 shows a two dimensional level set which is the convex hull of three ellipsoids.
Remark 3. In order to calculate the optimal value of $\gamma=\gamma^*(x)$,the LMI problem (5) needs to be solved. However,the calculation is a time-consuming process. Reference [23] provides a simplified way to get $\gamma^*(x)$.
Denote that $\alpha(\lambda,x)=x^{\rm T}\left(\lambda
Q_1+(1-\lambda))Q_2\right)^{-1}x$. Then,let $x \in \textbf{R}^n$
and $Q_1,Q_2 > 0$ be given. Assume that $Q_1-Q_2$ is nonsingular. Let $U \in {\bf R}^{n \times n}$ be such that $U^{\rm T}U=UU^{\rm
T}=I$ and $U^{\rm T}xx^{\rm T}U={\rm diag}\{x^{\rm
T}x,0,\ldots,0\}$. Let $\hat{Q}_1=U^{\rm T}Q_1U,\hat{Q}_2=U^{\rm
T}Q_2U$ and partition $\hat{Q}_1$ and $\hat{Q}_2$ as
$$\hat{Q}_1=[\hat{q}_1,\hat{Q}_{12}],\hat{Q}_2=[\hat{q}_2 \quad \hat{Q}_{22}],\hat{q}_1,\hat{q}_2 \in {\bf R}^{n \times 1}.$$
$${\rm{det}}\left[ {\matrix{
{\lambda ({{\hat Q}_{12}} - {{\hat Q}_{22}}) + {{\hat Q}_{22}}} & {{\rm{ }}{{\hat Q}_1} - {{\hat Q}_2}} \cr
{{0_{(n - 1) \times (n - 1)}}} & {\lambda {{({{\hat Q}_{12}} - \hat Q_{22}^{\rm{T}})}^{\rm{T}}} + \hat Q_{22}^{\rm{T}}} \cr
} } \right]{\rm{ }} = 0.$$
(6)
Remark 4. In this section,only two ellipsoids are used in (3). For this case,$Q_1-Q_2$ is nonsingular and $\gamma^*(x)$ can be easily calculated by the technology in Remark 3. Obviously,using more ellipsoids will make the conservatism less. However,for the case where $N > 2$,$\gamma^*(x)$ could be non unique in some special condition. Such as,the case that one of $Q_j$ might be the combined convex hull of other matrices,which may be considered as degenerated. Although,one can assume that there is no this kind of condition,it is hard to keep the uniqueness and continuity of $\gamma^*(x)$. Thus,for $N > 2$ case, it is difficult to compute the $\gamma^*(x)$ and needs further study.
B. Analysis of Attraction DomainAssume the set of ellipsoid $\Psi(P_j,\rho_j),j \in I[1,N]$ is given,the fractional order system can be invariant with a corresponding saturated linear feedback $Fx$. For simplicity and reducing the conservatism of the domain of attraction,a set of invariant ellipsoids $\Psi(P_j,\rho_j),j \in I[1,N]$ was considered with $\rho_j=1$.
Theorem 1. Suppose that the state
feedback law $F$ and an ellipsoid $\Psi(P_j),j \in I[1,N]$ are
given. If there exists a matrix $H_j \in \textbf{R}^{m \times n}$
satisfying
\begin{equation}\label{EQ:thm1}
\begin{split}
&(A+B(E_iF+E_i^{-}H_j))^{\rm T}P_j+P_j(A+B(E_iF+E_i^{-}H_j)) \\
&\qquad\le 0,\quad \forall i \in I[1,2^m],j \in I[1,N]
\end{split}
\end{equation}
(7)
Proof. From Lemma 5 we know,the following inequality needs to
be proved to ensure the asymptotic Mittag-Leffler stability of the
fractional order linear system (2)
corresponding the quadratic function (1),
\begin{equation}\label{Eq:Vtx}
D^{\alpha}V(t,x)=D^{\alpha}(x^{\rm T}P_jx) < 0,
\forall x \in \Psi(P_j,\rho) \setminus \{0\},
\end{equation}
(8)
\begin{equation}\label{EQ:xtpjx}
\begin{aligned}
D^\alpha(x^{\rm T}P_j&x) \le 2x^{\rm T}P_j(D^\alpha (x)) \notag \\
&=2x^{\rm T}P_j(Ax+BSat(Fx)) \notag \\
&=2x^{\rm T}A^{\rm T}P_jx + 2x^{\rm T}P_jB \sum_{i=1}^{2^m}\eta_{i}({E_iFx+E_i^{-}H_jx}),
\end{aligned}
\end{equation}
From Theorem 1,one can obtain that $D^\alpha(x^{\rm T}P_jx) <0$ for all $x\in \Psi(P_j,\rho) \backslash\{0\}$. And it is easy to notice that $Sat(Fx)$ is a convex hull of $E_iFx+E_i^{-}H_jx$ for all $i \in [1,2^m],j \in I[1,N]$ in (9). Thus,the Mittag-Leffler stability of the fractional order linear closed-loop system $D^\alpha x(t) = Ax(t) + BSat(Fx)$ is ensured.
The condition of $\Psi(P_j) \subset \Phi(H_j)$ is equivalent to $\rho h_{ji}P_j^{-1}h_{ji}^{\rm T} \le 1$,then it
can be written as follows by Schur complement,
$$\left[ {\matrix{
1 & {{h_{ji}}{{({{{P_j}} \over \rho })}^{ - 1}}} \cr
{{\rm{ }}{{({{{P_j}} \over \rho })}^{ - 1}}h_{ji}^{\rm{T}}{\rm{ }}} & {{{({{{P_j}} \over \rho })}^{ - 1}}} \cr
} } \right]{\rm{ }} \ge 0,$$
(9)
Denote $Q_j = ({\frac{P_j}{\rho}})^{-1}$. Let $G_j = H_j({\frac{P_j}{\rho}})^{-1}$ and the $i$-th row of matrix $G_j$ be $g_{ji}$,i.e.,$g_{ji} = h_{ji}({\frac{P_j}{\rho}})^{-1}$. Hence,the condition $\Psi(P_j,\rho) \subset \Phi(H_j),j \in I[1,N]$ can be formulated as,
$$\left[ {\matrix{
1 & {{g_{ji}}} \cr
{g_{ji}^{\rm{T}}} & {{Q_j}} \cr
} } \right]{\rm{ }} \ge 0{\rm{,for }}i \in [1,m],j \in I[1,N],$$
(10)
Let $G=\gamma_1 G_1+\gamma_2 G_2+\cdots+\gamma_N G_N$ and $g_{i}$ be
the $i$th row of $G$,combining inequality (7) and
inequality (10),gives
\begin{equation}
\begin{split}
Q(A+&BE_iF)^{\rm T}+(A+BE_iF)Q\\ &+G^{\rm T}E_i^-B^{\rm T}+BE_i^-G \le 0,\forall i \in [1,2^m],
\end{split}
\end{equation}
(11)
$$\left[ {\matrix{
1 & {{g_i}} \cr
{g_i^{\rm{T}}} & Q \cr
} } \right] \ge 0{\rm{,for }}i \in [1,m].$$
(12)
\begin{equation}
\begin{split}
&(A+B(E_iF+E_i^{-}H))^{\rm T}P+P(A+B(E_iF+E_i^{-}H)) \\ &\qquad\le 0,\,\forall i \in I[1,2^m],
\end{split}
\end{equation}
(13)
| $$\eqalign{ & \left[ {\matrix{ 1 & {{h_k}{{({P \over \rho })}^{ - 1}}} \cr {{{({P \over \rho })}^{ - 1}}h_k^{\rm{T}}} & {{{({P \over \rho })}^{ - 1}}} \cr } } \right] \ge 0,k \in I[1,m] \cr & \Leftrightarrow \Psi (P) \subset \Phi (H). \cr} $$ | (14) |
From the above fact,one can easily derive the conclusion that $\Psi(P)$ is invariant,which means that a trajectory starting from $x_0$ will stay inside of $\Psi(P_j)$ and it is a subset of $co\{\Psi(P_j),j \in I[1,N]\}$. Since that $x_0$ is a random point inside $co\{\Psi(P_j),j \in I[1,N]\}$,then one can obtain that the convex hull is an invariant set. If ``$<$'' holds for all the inequalities,then the state trajectory will converge to the origin for all the initial states.
Theorem 1 shows that if each $\Psi(P_j)$ is invariant,then,their convex hull,$co\{\Psi(P_j),j \in I[1,N]\}$ is also invariant. This theorem provides the sufficient condition for an ellipsoid to be inside the domain of attraction. To maximize the cross-section of the ellipsoid in the state-space $\textbf{R}^n$,the following type of convex set is considered in this paper:
\begin{equation*}
X_{R} = co \{ x_1,x_2,\ldots,x_l \},
\end{equation*}
\begin{equation}\label{supgammag}
\sup_{P_j>0,\rho,H_j} \lambda,
\end{equation}
(15)
$${\rm{s}}{\rm{.t}}{\rm{.}}\lambda {X_R} \subset \Psi ({P_j},\rho ),$$
(16)
$$\eqalign{
& {(A + B{E_i}F + E_i^ - {H_j})^{\rm{T}}}{P_j} \cr
& + {P_j}(A + B{E_i}F + E_i^ - {H_j}) < 0{\rm{,for }}i \in [1,{2^m}], \cr} $$
(17)
| \begin{equation}\label{infgamma} \inf_{Q_j>0,G} \Lambda, \end{equation} | (18) |
| $$\left[ {\matrix{ \Lambda & {x_{ji}^{\rm{T}}} \cr {{x_{ji}}} & {{Q_j}} \cr } } \right] \ge 0{\rm{,for }}i \in [1,l],j \in I[1,N],$$ | (19) |
| \begin{align} & Q_jA^{\rm T} + AQ_j +BE_i^{-1}G_j + G_j^{\rm T}{(BE_i^{-1})}^{\rm T} \notag \\ &+ Q_j(BE_iF)^{\rm T}+ (BE_iF)Q_j \mbox{,for } i\in [1,2^m],\label{constraintb2} \end{align} | (20) |
where $\Lambda=\frac{1}{\lambda^2}$,$Q_j = ({\frac{P_j}{\rho}})^{-1}$,$G_j = H_j({\frac{P_j}{\rho}})^{-1}$.
Ⅳ. Controller SynthesisIn this section,the possibility that a level set can get invariant with controls subject to actuator saturation is investigated. Then,a continuous feedback law that guarantees the invariance of the convex hull of ellipsoids $co\{\Psi(P_j),j \in I[1,N]\}=L_{V_c}(1)$ is constructed.
Considering the fractional order system $D^\alpha(x)=Ax+BSat(u)$,where $0<\alpha<1$. Only the initial condition needs to be specified. For $x_0$,the state trajectory of system (2) is defined as $\psi(t,x_0)$. Then the domain of attraction of the origin is
| \begin{equation*} \varPsi := \{x_0 \in \textbf{R}^n: \lim_{t \rightarrow \infty}\psi(t,x_0)=0 \}. \end{equation*} |
Denote $P\in \textbf{R}^{n \times n}$ be a positive-definite matrix and $V_c(x)=x^{\rm T}Px$ as Lyapunov function of fractional order system (2). Then,the ellipsoid $\Psi(P,\rho) = \{x\in \textbf{R}^{n}: x^{\rm T}Px\le \rho\}$ is said to be (contractively) invariant if $D^{\alpha}V(x)<0$ for all $x \in \Psi(P,\rho) \backslash \{0\}$,and then ellipsoid $\Psi(P^*,\rho)$ is called the invariant set of fractional order systems (2). Let $\rho=1$,hence,if the ellipsoid $\Psi(P)$ is contractive invariant set,it is inside the domain of attraction.
Fact 1 [25] For a raw vector $f_0 \in \textbf{R}^{1
\times n}$ and matrix $P>0$,$\Psi(P) \subset \Phi(f_0)$ if and only
if,
$${f_0}{P^{ - 1}}f_0^{\rm{T}} \le 1 \Leftrightarrow {\rm{ }}\left[ {\matrix{
1 & {{f_0}{P^{ - 1}}} \cr
{{P^{ - 1}}f_0^{\rm{T}}} & {{P^{ - 1}}} \cr
} } \right] \ge 0.$$
Theorem 2. Assuming that each of ellipsoids $\Psi(P_j),j \in I[1,N]$ is contractively invariant. Then,as a result,the level set $L_{V_c}(1)$ is also contractively invariant.
Proof. The proof of invariance is as follows. Let $V_j(x)=x^{\rm T}P_jx$. Assuming there exists a $u_j \in \textbf{R}^m,|u_j|_\infty \le 1$ such that
| \begin{equation}\label{EQ:xtjpjxj} D^\alpha(x^{\rm T}_jP_jx_j) \le 2x^{\rm T}_jP_j(Ax_j+BSat(u_j)) \le 0. \end{equation} | (21) |
As the fact that if $D^{\alpha}V_j(x)<0$ for all $x \in \Psi(P_j) \backslash \{0\}$,and then ellipsoid $\Psi(P_j)$ is said to be invariant. From Lemma 2,we know,
$$D^\alpha(X^{\rm T}_jP_jx_j) \le 2x^{\rm T}_jP_jD^\alpha(x_j),$$
$$2x^{\rm T}_jP_jD^\alpha(x_j) \le 0,$$
Let $r_0=(P_0x_0)^{\rm T}$,$x_0 \in \mathcal{L}_{V_c}(1)$,where $\mathcal{L}_{V_c}(1)$ is the edge of $L_{V_c}(1)$. Then we get $r_0x_0=x^{\rm T}_0P(\gamma^*(x_0))x_0=1$,which means the hyperplane $r_0x=1$ is tangential to the convex set $L_{V_c}(1)$ at $x_0$. Then the level set $L_{V_c}(1)$ lies between $r_0x=1$ and $r_0x=-1$,therefore
$$\Psi(P_j) \subset \Phi(r_0) \forall j \in I[1,N_0],$$
$$1=r_0x_0 \ge r_0x_j.$$
\begin{align*}
1=\,&r_0x_0=\xi_1r_0x_1+\sum^{N_0}_{j=2}\xi_jr_0x_j\\
\le\,& \xi_1r_0x_1+\sum^{N_0}_{j=2}\xi_j \le \sum^{N_0}_{j=1}\xi_j=1,
\end{align*}
| $$r_0^{\rm T}=P_jx_j \quad \forall j \in I[1,N_0].$$ |
By inequality (21) and the assumption we know,there exists a $u_j \in \textbf{R}^m,|u_j|_\infty<1$ such that inequality (21) is satisfied. Let $u_0=\displaystyle{\sum_{j=1}^{N_0}}\xi_ju_j$. Then,by $|u_0|_\infty \le 1$ and by the convexity,
$$D^\alpha(x^{\rm T}_0P_0x_0) \le 2r_0(Ax_0+BSat(u_0)) \le 0.$$
Theorem 3. Consider ellipsoid $\Psi(P_j)$ and
feedback matrices $F_j \in \textbf{R}^{m \times n}$. For the
closed-loop fractional order system (2), if
the ellipsoid type convex set $X_R$ is considered,then the state
feedback matrix $F_j\in \textbf{R}^{m \times n}$ can be obtained as
$F_j=Y_jQ_j^{-1}$,where $Y_j,Q_j$ are solutions of the following
optimization problem:
\begin{equation}\label{infgammaF}
\inf_{Q_j>0,Y_j,G_j} \Lambda,
\end{equation}
\begin{equation*}\label{constraint3ac}
\mbox{s.t. } (10),(19),\mbox{ and}
\end{equation*}
(22)
\begin{align}
& Q_jA^{\rm T} + AQ_j +BE_i^{-1}G_j + G_j^{\rm T}{(BE_i^{-1})}^{\rm T} \notag \\
&+ Y_j^{\rm T}E_i^{\rm T}B^{\rm T}+ BE_iY_j \le 0 \mbox{,for } i\in [1,2^m],j\in [1,N].\label{constraintb3}
\end{align}
(23)
\begin{equation}
Y(\gamma)=\displaystyle{\sum_{j=1}^N}\gamma_jY_j,\quad
Q(\gamma)=\displaystyle{\sum_{j=1}^N}\gamma_jQ_j,
\end{equation}
(24)
Proof. Let $G_j=Q_jH_j$,$G(\gamma)=\sum_{j=1}^N\gamma_jG_j$
and $H(\gamma)=G(\gamma)Q^{-1}(\gamma)$,give
\begin{align}
& Q(\gamma)A^{\rm T} + AQ(\gamma) +BE_i^{-1}G(\gamma) + G(\gamma)^{\rm T}{(BE_i^{-1})}^{\rm T} \notag \\
&\qquad+ Y(\gamma)^{\rm T}E_i^{\rm T}B^{\rm T}+ BE_iY(\gamma) \le 0,\label{constraintb4}
\end{align}
(25)
\begin{equation}
\begin{split}\label{ineq}
&(A+B(E_iF(\gamma)+D_i^-H(\gamma)))^{\rm T}P(\gamma)\\&\qquad+P(\gamma)(A+B(E_iF(\gamma)+D_i^-H(\gamma)))\\&\qquad \le 0,\,\forall i \in I[1,2^m].
\end{split}
\end{equation}
(26)
We use an example of [22] to illustrate the effectiveness of our method. For fractional order linear systems (2),let $\alpha=0.7$,and
$$A = \left[ {\matrix{
{0.7} & { - 1.4} \cr
{ - 0.2} & {1.5} \cr
} } \right],B = \left[ {\matrix{
1 & 0 \cr
0 & 1 \cr
} } \right].$$
$$X_R=co\{x,-x\},$$
$${P_1} = \left[ {\matrix{
{4.7515} & { - 0.3347} \cr
{ - 0.3347} & {2.2345} \cr
} } \right],{P_2} = \left[ {\matrix{
{0.2985} & { - 0.5538} \cr
{ - 0.5538} & {2.9894} \cr
} } \right].$$
|
Download:
|
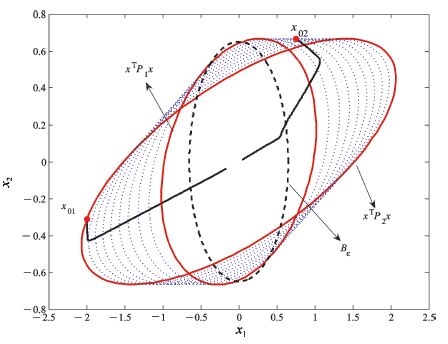
| Fig. 2 Comparison between proposed method and existing method [22] . | |
The convex combination of $P_1$ and $P_2$ in Fig. 2 shows that the proposed method provides a satisfactory estimation on the domain of attraction and also can obtain better estimation that the approach in [22].
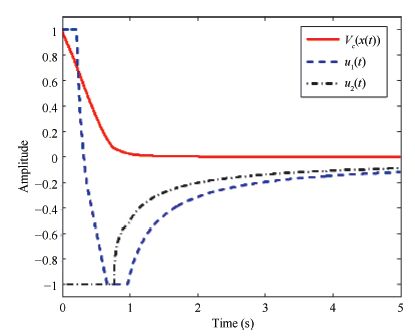
Remark 5. From Fig. 2 we know,the closed-ball $B_\epsilon$ which proposed in [22] is almost contained in the convex hull of the proposed method. Two state trajectories started from initial points $x_{01}=[-2 -0.3127],x_{02}=[0.75 0.6665]$ on the boundary of $L_{V_c(1)}$ shows that,the trajectories are convergent to origin , and the proposed method provides better estimation on the domain of attraction than method in [22]. This method extend the domain of attraction. The control signals $u_1(t)$,$u_2(t)$ and the Lyapunov function $V_c(x(t))$ of example 1 are illustrated in Fig. 3. Comparative example indicates that the proposed method is less conservative than [22].
|
Download:
|
| Fig. 3 Signals $u_1(t)$,$u_2(t)$ and the Lyapunov function $V_c(x(t))$. | |
In this paper,we consider the fractional order system with
$$\alpha = 0.9,A = \left[ {\matrix{
{1.6} & { - 0.5} \cr
{ - 0.6} & {0.6{\rm{ }}} \cr
} } \right]{\rm{ }},B = \left[ {\matrix{
5 \cr
{ - 5} \cr
} } \right].$$
$$X_R=co\{x_i,-x_i\},\,i=1,2,$$
$$F_1=[-0.0414\quad-0.2897],\quad F_2=[0.2161\quad-0.3540],$$
| $${P_1} = \left[ {\matrix{ {0.7985} & {0.188} \cr {10.1881} & {0.1270} \cr } } \right],{P_2} = \left[ {\matrix{ {1.6258} & {0.1881} \cr {0.1881} & {0.0443} \cr } } \right].$$ |
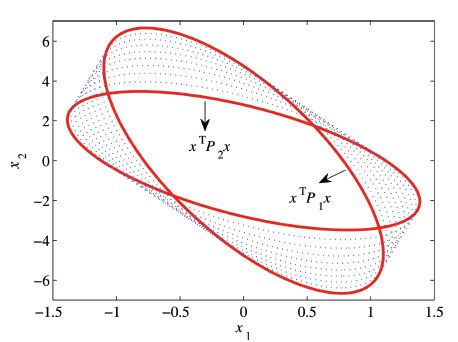
The matrix $P_1$ and $F_1$ are designed such that the closed-loop system (2) is locally Mittag-Leffler stable and the estimated ellipsoid invariant set is maximized with respect to the bounded convex set $X_R$. Similarly,the matrix $P_2$ and $F_2$ are designed such that $\lambda X_R \subset \Psi(P)$. The boundaries of the two ellipsoids are plotted in red solid curves,while the dotted curves are the boundaries of $\Psi(P(\gamma))$ as $\gamma$ varies in the set $\Gamma$. The shape of $L_{V_c}(1)=\bigcup_{\gamma \in \Gamma}\Psi(P(\gamma))$ can be obtained by those blue dotted curves in Fig. 4. The $\gamma^*(x)$ can be obtained by computing the optimization problem (4) or the formula in (6).
|
Download:
|
| Fig. 4 Convex hull of two provided ellipsoids. | |
From Theorem 2. we know,
$$F(\gamma^\ast)=(\gamma^\ast Y_1+(1-\gamma^\ast) Y_2 )(\gamma^\ast Q_1+(1-\gamma^\ast) Q_2)^{-1},$$
$${Y_1} = \left[ {\matrix{
{ - 0.9000} & {1.7921} \cr
} } \right],{Y_2} = \left[ {\matrix{
{ - 0.9000} & {5.9397} \cr
} } \right],$$
$${Q_1} = \left[ {\matrix{
{1.9228} & { - 2.8469} \cr
{ - 2.8469} & {12.0873} \cr
} } \right]{\rm{ }},{Q_2} = \left[ {\matrix{
{1.2087} & { - 5.1320} \cr
{ - 5.1320} & {44.3652} \cr
} } \right].$$
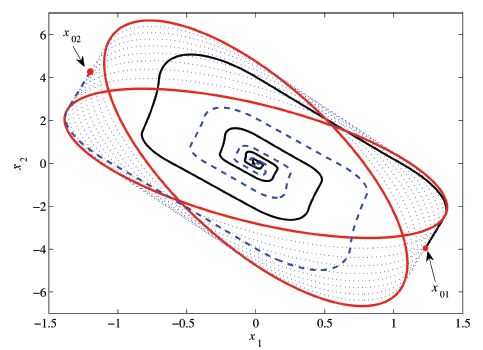
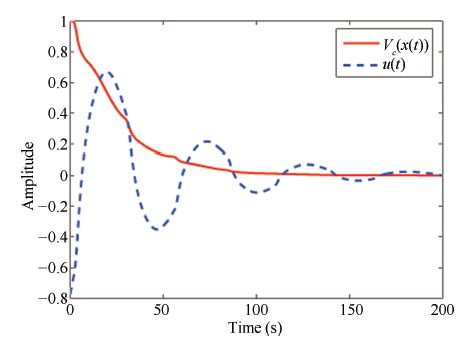
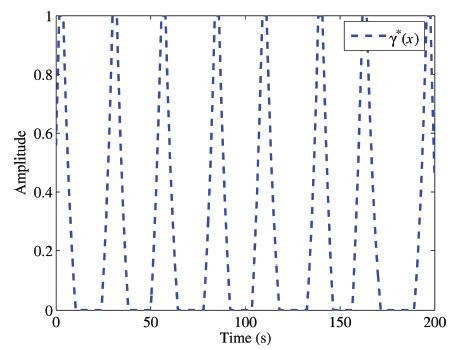
Fig. 5 shows that the state trajectories with different initial conditions. Obviously,the closed-loop system (2) is asymptotically Mittag-Leffler stable. To obtain the control signal and the composite quadratic function,the state trajectory from initial point $x_{01}=[1.2300\,\,-3.9533]$ and $x_{02}=[-1.200\,\,4.2699]$ started from the boundary of level set $L_{V_c}(1)$ is illustrated in Fig. 5. The control signal $u(t)$ and the Lyapunov function $V_c(x(t))$ of trajectory started from $x_{01}$ are demonstrated in Fig. 6,and the value of $\gamma^{\ast}(x)$ is plotted in Fig. 7 as $x(t)$ varies along the time.
|
Download:
|
| Fig. 5 State trajectory with different initial conditions. | |
|
Download:
|
| Fig. 6 Control signal $u(t)$ and the Lyapunov function $V_c(x(t))$. | |
|
Download:
|
| Fig. 7 $\gamma^{\ast}(x)$ varies in $[0, 1]$. | |
This paper provides a method for the estimation of the domain of attraction and state feedback synthesis utiize the convex combination form for fractional order systems subject to actuator saturation with the fractional order $0<\alpha<1$. The ellipsoidal invariant set of fractional order systems subject to actuator saturation is investigated by convex hull form for the first time. Then we demonstrate that the convex hull of ellipsoids can be made invariant for fractional order linear systems subject to actuator saturation if each ellipsoid in a set with a bounded control of the saturating actuators is invariant. The results show that the proposed method is effective to handle saturation nonlinearity. The composite quadratic Lyapunov function and Lyapunov direct approach are applied in this paper to estimate the invariant ellipsoids for fractional order systems. In particular,by using a set of feedback laws to make the convex hull of a set of ellipsoid invariant,one proper method is proposed to construct a continuous feedback law.
In order to facilitate analysis,the case $N=2$ is chosen in this paper. A more effective way needs to be specified to compute the condition $N > 2$. Nevertheless,the stability analysis problem for fractional order system subject to actuator saturation with the fractional order $1 < \alpha <2$ is still unsolved. The stability conditions for fractional order systems is concerned with the fractional order,thus our future work is related to the problem of order-dependent estimation on the domain of attraction.
| [1] | Sabatier J, Agrawal O P, Machado J A T. Advances in Fractional Calculus. Netherlands: Springer, 2007. |
| [2] | Mainardi F. Fractional calculus. Fractals and Fractional Calculus in Continuum Mechanics. Vienna: Springer, 1997. 291-348 |
| [3] | Meral F C, Royston T J, Magin R. Fractional calculus in viscoelasticity: an experimental study. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(4): 939-945 |
| [4] | Baleanu D, Golmankhaneh A K, Golmankhaneh A K, Baleanu M C. Fractional electromagnetic equations using fractional forms. International Journal of Theoretical Physics, 2009, 48(11): 3114-3123 |
| [5] | Luo Y, Chen Y Q. Fractional order [proportional derivative] controller for a class of fractional order systems. Automatica, 2009, 45(10): 2446-2450 |
| [6] | Luo Y, Chen Y Q. Stabilizing and robust fractional order PI controller synthesis for first order plus time delay systems. Automatica, 2012, 48(9): 2159-2167 |
| [7] | Kheirizad I, Jalali A A, Khandani K. Stabilization of all-pole unstable delay systems by fractional-order [PI] and [PD] controllers. Transactions of the Institute of Measurement and Control, 2013, 35(3): 257-266 |
| [8] | Hu T S, Lin Z L, Chen B M. An analysis and design method for linear systems subject to actuator saturation and disturbance. Automatica, 2002, 38(2): 351-359 |
| [9] | Zhang L X, Boukas E K. Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica, 2009, 45(2): 463-468 |
| [10] | Ma S, Zhang C, Zhu S. Robust stability for discrete-time uncertain singular Markov jump systems with actuator saturation. IET Control Theory & Applications, 2011, 5(2): 255-262 |
| [11] | Chen Y Q, Moore K L. On Dα-type iterative learning control. In: Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, FL: IEEE, 2001. 4451-4456 |
| [12] | Li Y, Chen Y, Ahn H S. Fractional order iterative learning control. In: Proceedings of the ICCAS-SICE 2009. Fukuoka, Japan: IEEE, 2009. 3106-3110 |
| [13] | Li Y, Chen Y Q, Ahn H S. Fractional-order iterative learning control for fractional-order linear systems. Asian Journal of Control, 2011, 13(1): 54-63 |
| [14] | Lu J G, Chen Y Q. Stability and stabilization of fractional-order linear systems with convex polytopic uncertainties. Fractional Calculus and Applied Analysis, 2013, 16(1): 142-157 |
| [15] | Li C, Wang J C. Robust stability and stabilization of fractional order interval systems with coupling relationships: the 0 < α < 1 case. Journal of the Franklin Institute, 2012, 349(7): 2406-2419 |
| [16] | Lu J G, Ma Y D, Chen W D. Maximal perturbation bounds for robust stabilizability of fractional-order systems with norm bounded perturbations. Journal of the Franklin Institute, 2013, 350(10): 3365-3383 |
| [17] | Liao Z, Peng C, Li W, Wang Y. Robust stability analysis for a class of fractional order systems with uncertain parameters. Journal of the Franklin Institute, 2011, 348(6): 1101-1113 |
| [18] | Jiao Z, Zhong Y S. Robust stability for fractional-order systems with structured and unstructured uncertainties. Computers & Mathematics with Applications, 2012, 64(10): 3258-3266 |
| [19] | Li Y, Chen Y Q, Podlubny I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica, 2009, 45(8): 1965-1969 |
| [20] | Yu J M, Hu H, Zhou S B, Lin X R. Generalized Mittag-Leffler stability of multi-variables fractional order nonlinear systems. Automatica, 2013, 49(6): 1798-1803 |
| [21] | Li C, Wang J, Lu J. Observer-based robust stabilisation of a class of nonlinear fractional-order uncertain systems: an linear matrix inequalitie approach. IET Control Theory & Applications, 2012, 6(18): 2757-2764 |
| [22] | Lim Y H, Oh K K, Ahn H S. Stability and stabilization of fractionalorder linear systems subject to input saturation. IEEE Transactions on Automatic Control, 2013, 58(4): 1062-1067 |
| [23] | Hu T S, Lin Z L. Composite quadratic Lyapunov functions for constrained control systems. IEEE Transactions on Automatic Control, 2003, 48(3): 440-450 |
| [24] | Duarte-Mermoud M A, Aguila-Camacho N, Gallegos J A, Castro-Linares R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Communications in Nonlinear Science and Numerical Simulation, 2015, 22(1-3): 650-659 |
| [25] | Hu T S, Lin Z L. Control Systems with Actuator Saturation: Analysis and Design. Basel: BirkhÄauser, 2001. |
| [26] | Li C, Lu J G. On the ellipsoidal invariant set of fractional order systems subject to actuator saturation. In: Proceedings of the 34th Chinese Control Conference. Hangzhou, China: IEEE, 2015. 800-805 |
| [27] | Li C, Wang J C, Lu J G, Ge Y. Observer-based stabilisation of a class of fractional order non-linear systems for 0 < α < 2 case. IET Control Theory & Applications, 2014, 8(13): 1238-1246 |
 2016, Vol.3
2016, Vol.3 


