2. Institute of Intelligent Machines, Chinese Academy of Sciences
Singing voice is probably the first musical instrument as it exists prior to the invention of any other instrument. Singing voice synthesis,which enables computer to sing like a human,has been a subject of research for more than 50 years[1],and the quality which can be obtained now opens new perspectives.
There are mainly two types of singing voice synthesis systems currently. One is concatenative singing voice synthesis (CSVS)[2, 3]. A typical CSVS application is the vocaloid synthesizer[4]. CSVS concatenates sample units from a singing voice corpus,it succeeds in capturing the naturalness of the sound. However,the lack of flexibility and requirement of very large corpus are two of the main problems. The other one is hidden Markov model (HMM) based singing voice synthesis (HMMSVS). In recent years, HMM-based speech synthesis technique[5, 6] developed rapidly, and has been applied to various applications such as singing voice synthesis. The main advantages of HMMSVS is flexibility in changing its voice characteristics . Besides,SPSVS also has a very small footprint. The first HMMSVS is Sinsy[7, 8, 9, 10],which supports Japanese and English currently.
For mandarin Chinese,there have been several work before. Zhou et al.[11] built a mandarin Chinese CSVS system. Li et al.[12] implemented F0 and spectrum modification module as back-end of text-to-speech system to synthesize singing voice. Gu et al.[13] used harmonic plus noise model (HNM) to design a scheme for synthesizing a mandarin Chinese singing voice. Recently,a mandarin Chinese HMMSVS was proposed[14].
We focus on mandarin Chinese HMMSVS in this paper. Although there was a mandarin Chinese HMMSVS before[14],our system has the following different features:
1) We solve the data sparse problem and handle the situation of melisma at the same time inside the HMM-based framework.
2) A recent advance in speech synthesis technique,the multi level F0 model[15, 16, 17] is used to overcome over-smoothing of generated F0 contour.
The major difference between read speech and singing voice is that singing should obey the pitch and rhythm of the musical score,and pitch and rhythm also have a great impact on the subjective quality of synthesized singing voice. In our system,precise rhythm is guaranteed by modeling time-lag using timing model[7].
Two methods are used to improve the F0 generation. One is single Viterbi training,after the conventional model training,Viterbi is performed to get state level alignment,and a single training is performed to model the difference between F0 of singing voice and that of musical score. This method can not only solve the data sparse problem,but also handle the situation of melisma. The other one is generating F0 with two levels. F0 of musical score is subtracted from F0 contour and then the residual F0 contour is parameterized by discrete cosine transforms (DCT) at syllable level. Context-dependent HMMs (CD-HMMs) are then trained for syllable DCT coefficients. At generation,state-level DF0 model and syllable-level DCT model are integrated to generate F0 contour. The two level method can overcome over-smoothing and generate more expressive F0 contour. Besides,vibrato is also extracted and modeled[9] by CD-HMMs in our system.
Objective and subjective evaluations are conducted to evaluate the performance of the proposed system. For objective evaluation,we define a new measurement called mean note distance (MND) based on the sense of music,MND is calculated by measuring the distance of each note pair in two F0 contours. It can measure whether the two sequences of note are "in tune".
The rest of this paper is organized as follows: related previous work is presented in Section Ⅱ,description of the proposed system is given in Section Ⅲ,Section Ⅳdescribes the proposed improved F0 models,Section Ⅴ shows experimental results,and conclusions are given in Section Ⅶ.
Ⅱ. PREVIOUS WORK A. HMM-based FrameworkFig. 1 shows the flowchart of HMM-based speech synthesis system.

|
Download:
|
| Fig. 1. Flowchart of the HMM-based speech synthesis system. | |
In mandarin Chinese,each syllable consists of one initial and one final or only one final. And initial/final is usually used as model unit in speech synthesis. Each initial/final is modeled by a left-to-right and no skip structure HMM.
At feature extraction stage,F0 and spectral features are extracted from waveforms. In addition to the static features,velocity and acceleration features are appended. Let ${\pmb X}_t=[{\pmb x}_t,$ $\Delta {\pmb x}_t,{\Delta}^2 {\pmb x}_t],$ $\Delta {\pmb x}_t = 0.5 \ast ({\pmb x}_{t+1}-{\pmb x}_{t-1}),$ ${\Delta}^2{\pmb x}_t=-2.0\ast{\pmb x}_{t-1}$ $+$ ${\pmb x}_t+2.0\ast{\pmb x}_{t+1}$, and ${\pmb x}=[{\pmb x}_1,{\pmb x}_2,...,{\pmb x}_t]^{\rm T}$ is static feature sequence,${\pmb X}=[{\pmb X}_1,{\pmb X}_2,...,{\pmb X}_T]^{\rm T}$ is observation feature sequence, $\pmb X$ can be written as $\pmb X= W \pmb x$,where $ W$ is a matrix determined by the way of calculating velocity and acceleration features. In addition to acoustic features,contextual features are also extracted for training.
During training,F0 and spectrum are modeled with multi-stream HMM,among them F0 stream is modeled with multi-space probability distributions HMM[18]. A set of context-dependent HMMs $\pmb \lambda$ are estimated by maximizing the likelihood function,and then a decision tree is built to cluster all HMM states based on contextual features using the minimum description length (MDL) criterion[19]. State duration model is also trained at this stage.
During synthesis,label consisting of designed contextual features is obtained by linguistic analysis on the input text,state duration model is then used to determine state sequence. And then F0 and spectral parameters are generated by the maximum likelihood parameter generation (MLPG) algorithm[20] using state-level F0 and spectrum models.
| \begin{align} \hat{\pmb x} &=\arg\max\limits_{\pmb x} P( W \pmb x|\pmb \lambda)\notag\\ &=\arg\max\limits_{\pmb x} P( W \pmb x|\pmb \lambda)P(\pmb q|\pmb \lambda,l), \end{align} | (1) |
where $l$ is the input label,$\pmb q=[q_1,q_2,...,q_t]$ is state sequence determined by $l$ and duration model. By equating $\frac{\partial {\log}P( W \pmb x| \pmb \lambda)}{\partial \pmb x}$ to $\pmb 0$,speech parameters are generated by solving the linear equation (2). Because $ W^{\rm T} \Sigma^{-1} W$ has a positive-definite band-symmetric structure,this equation can be solved efficiently by using cholesky decomposition.
| \begin{align} W^{\rm T} \pmb U^{-1} W \hat{\pmb x} = W^{\rm T} \pmb U^{-1}\pmb M, \end{align} | (2) |
| \begin{align} \pmb U={\rm diag}\{ \Sigma_{q_1},...,\Sigma_{q_T}\}, \end{align} | (3) |
| \begin{align} \pmb M=[\pmb \mu_{q_1},...,\pmb \mu_{q_T}]^{\rm T}, \end{align} | (4) |
where $T$ is the number of frame,$\pmb \mu_{q_t}$ and $ \Sigma_{q_t}$ are the mean vector and covariance matrix of $q_t$-th state respectively.
At last,the mel log spectrum approximation (MLSA)[21] filter is used to synthesize voice with the generated parameters.
B. HMM-based Singing Voice SynthesisThe first HMM-based singing voice system is Sinsy[7, 8, 9, 10], which supports Japanese and English currently. Sinsy made some modifications to HMM-based speech synthesis framework for the purpose of singing voice synthesis.
First,duration model in speech synthesis is not appropriate for singing voice any more,because singing voice should obey the rhythm in the musical score. However,if duration strictly obey the musical score,the synthetic singing voice would be unnatural, because there is time-lag between start time of the notes on musical score and real singing voice. In Sinsy,time-lag was modeled by Gaussian distribution.
Second,F0 of singing voice data is always sparse because large amount of contexts,i.e.,key,pitch of note etc. So HMMs that hardly ever appear in the training data cannot be well trained. Pitch pseudo training[8] has been proposed to address this problem,but there are several problems with pitch pseudo training, for example,the features included in a specific pitch range cannot be modeled since the pitch contexts are mixed due to pitch-shifted pseudo-data[10]. Pitch pseudo training is not a good solution, so other methods which model difference between F0 of singing voice and that of musical score have been proposed[10, 22]. Data-level normalization method[22] modeled the difference between F0 of singing voice and that of musical score by doing normalization before training. Although F0 is sparse,it is around the F0 value of the musical note,so the difference is not sparse and data sparse problem can be solved. The problem of data-level normalization method is it need to be trained by fixing the label, or there will be inconsistency between data and training. However, fixing the label,models cannot be well trained unless labels are perfectly right. In most cases,there exists errors in labels. Oura et al.[10] proposed pitch adaptive training which does F0 normalization at model level using speaker adaptive training technique[23].
| \begin{align} \mu_i&= B_i \pmb \epsilon= \hat{\mu}_i + b_i, \end{align} | (5) |
where $b_i$ is F0 value of note corresponding to the $i$-th state, the transformation matrix $ B_i=[1,b_i]$ is fixed by musical sore, and $\hat{\mu_i}$ is the only parameter need to be estimated. In this way,normalization of F0 is done at model level,there is no need to fix the label during training.
Third,Sinsy also added a vibrato stream to synthesize vibrato[9]. In HMM-based framework,synthesized F0 contour is smooth,so vibrato cannot be synthesized. In Sinsy,F0 of singing voice was represented as a sum of two components,intonation component $m(t)$,which corresponds to the melody of musical score,and vibrato component $v(t)$,which is an almost sinusoidal modulation. As is shown in equation (6),$v_e(t)$ is vibrato extent and $v_r(t)$ is vibrato rate.
| \begin{align} F0(t)&= m(t) + v(t)\notag\\ &= m(t) + v_e(t)\cos\left(\frac{2 \pi v_r(t)t}{f_s}\right), \end{align} | (6) |
where $f_s$ is sampling frequency of the F0 contour. Vibrato area was detected and vibrato parameters are extracted[24],and then vibrato parameters were modeled by context-dependent HMMs such as F0 and spectrum.
Recently,a HMM-based mandarin singing voice synthesis system was proposed[14]. In this system,pitch pseudo training was used to address data sparse problem of F0,vibrato was synthesized at a constant vibrato rate during note.
C. ProblemsIn addition to the data sparse problem,there are two problems to be solved for F0.
In mandarin Chinese singing voice,a syllable may contains one note or more than one notes. The situation of singing of a single syllable while moving between several different notes in succession is called melisma1. The situation of melisma is not discussed in pitch adaptive training approach[10]. In Cheng's approach[14],melsima is synthesized by repeating the last final in previous words to mimic the singing skill. However,this approach,which is usually used in CSVS,has the problem of discontinuity.
1http://en.wikipedia.org/wiki/Melisma
One of the drawback of HMM-based synthesis system is that generated parameter trajectory is usually over-smoothed,this is a more serious problem for singing voice,because F0 of singing voice is always more dynamic[25]. Higher-level F0 model based on DCT combined with state-level model[15, 16] has been used to overcome the over-smoothing of generated F0 contour in speech synthesis. We apply syllable level DCT model to singing voice synthesis in this paper.
Ⅲ. DESCRIPTION OF THE PROPOSED SYSTEM A. Database Creation1) Database design and recording. The songs for singing database were selected from children and traditional pop songs. Four criterions were used for the selection of songs:
a) coverage of all syllables;
b) balance of initial/final;
c) coverage and balance of key;
d) coverage and balance of tempo.
After selecting songs,MIDI files were recorded through a MIDI keyboard connected to a computer. MIDIs and lyrics were then combined to save in the format of LilyPond[26],a professional music notation environment and software. Fig. 2 shows a example of the musical score format.

|
Download:
|
| Fig. 2. An example of musical score format. | |
A professional male singer was invited for recording the database. All the songs were recorded along with a metronome. The overview of the database is summarized in Table Ⅰ.
|
|
TABLE Ⅰ OVERVIEW OF THE DATABASE |
2) Contextual features. The synthetic singing voice should represent both precise lyric information and musical information,so both the above two should be included in contextual features. We design a four-level contextual features for our system:
a) initial/final level:
i) current initial/final;
ii) preceding and succeeding intial/final.
b) note level (or syllable level):
i) absolute pitch;
ii) relative pitch;
iii) pitch difference between current note and preceding note;
iv) pitch difference between current note and succeeding note;
v) length of preceding,current and succeeding note (thirty-second note,millisecond);
vi) position of current note in musical bar;
vii) position of current note in musical phrase;
viii) melisma or not,absolute pitch of the last note in melisma, difference between the pitch of the first note and the last note in melisma.
c) phrase level:
i) number of notes in current phrase;
ii) length (thirty-second note);
iii) length (millisecond).
d) song level:
i) key,time signature and tempo;
ii) number of notes;
iii) length (millisecond);
iv) length(thirty-second note).
For each musical score (lyrics included),we analysis it to obtain full contextual features.
B. System FrameworkThe framework of the proposed singing synthesis system is shown in Fig. 3. The modules in solid lines represent the baseline system, these are similar with the system described in Section Ⅱ-A,except for an additional timing model and an additional vibrato stream. The modules in dash lines are the improved F0 models in the proposed system,details of these modules are described in Section Ⅳ.

|
Download:
|
| Fig. 3. Flowchart of the HMM-based singing voice synthesis system (The modules in solid lines represent the baseline system; the modules in dash lines is the improved F0 models in the proposed system; CD-HMMs means context-dependent HMMs). | |
Initial/final is used as model unit,and modeled by HMM with a left-to-right and no skip structure. Vibrato is modeled simultaneously with F0 and stream using multi-stream HMMs. After conventional training,syllable alignment and state alignment are obtained using the trained models to align the training data. State alignment is then used to perform a single Viterbi training to model the difference between F0 of musical score and singing voice. Syllable alignment is used to train the timing model[7] to obtain a precise rhythm,and syllable level DCT F0 model is also trained.
During synthesis,label consisting of contextual features is obtained by analysis on musical score. The timing model combined with state duration model are then used to determine the HMM sequence[7]. And then F0 and spectral parameters are generated. Details of the proposed F0 generation methods are described in Section Ⅳ.
Ⅳ. IMPROVED F0 MODEL A. DF0 ModelIn the case of melisma,the model(initial/final) may range over several different notes,thus the transformation matrix in (5) cannot be fixed by musical score directly,so pitch adaptive training[10] is not suitable for the proposed system.
Our method can handle the situation of melisma. As is shown in Fig. 4,the difference between F0 of singing voice and musical score is modeled. After the conventional model training:
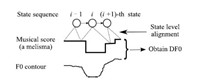
|
Download:
|
| Fig. 4. Single Viterbi training, state sequence is aligned, and then DF0 is obtained and trained for each corresponding state. Each state may range over more than one notes at the situation of melisma. | |
1) Viterbi is performed to get state sequence.
2) F0 vector of musical score is generated according to state sequence and musical score. F0 value of each is calculated by
| \begin{align*} f=440\times2^\frac{MIDINOTE-69}{12}.\end{align*} |
Duration of each note is determined by state sequence. In the case of melisma,duration of each notes in the melisma is calculated by
| \begin{align*} d_i=\frac{L_i}{\sum L_i}d,\end{align*} |
where $d$ is duration of the whole note determined by state sequence,$d_i$ is calculated duration of $i$-th note,and $L_i$ is musical length (e.g.,1/4, 1/8) of $i$-th note.
3) The difference between F0 of singing voice and that of musical score (DF0) is obtained frame by frame.
4) There are two ways to model DF0.
a) DF0-A: State-level alignment is obtained,so $DF0$ can share the decision trees with F0,and is modeled by a gaussian model at each leaf node.
b) DF0-B: DF0 is modeled separately with other parameters,under the HMM-based framework. It has its own decision tree and duration model.
During generation,first,state sequence $\pmb q$ is determined, and then the F0 vector of musical score $\pmb M^{S}$ can be generated according to musical score and state sequence. Here the vector $\pmb M$ in (2) is the sum of two parts,$\pmb M^{DF0}$ and $\pmb M^{S}$.
| \begin{align} \pmb M^{F0}=\pmb M^{DF0} + \pmb M^{S}. \end{align} | (7) |
Finally,the MLPG algorithm is performed to generate F0 contour.
This method is a special form of speaker adaptive training. It performs a single Viterbi training,and the transformation matrix is fixed by musical score and aligned state-level label simultaneously.
B. Syllable-level Model1) Discrete cosine transform for F0. DCT has been successfully used for modeling F0 in several languages[15, 16, 17] before. And it was also used for characterizing F0 of singing voice[27, 28]. DCT is a linear,invertible function. It uses a sum of cosine functions to express a finite F0 contour. The Type-II DCT is used in this paper,
| \begin{align} &c_n=\frac{\sqrt 2}{T} \alpha_n \sum_{t=0}^{T-1} f_t {\rm cos}\left\{\frac{\pi}{T}n\left(t+\frac{1}{2}\right)\right\},\notag\\ &\qquad\qquad\qquad\qquad\qquad\qquad n=0,1,...,N-1,\end{align} | (8) |
| ${\alpha _n} = \left\{ \begin{array}{l} \frac{1}{{\sqrt 2 }},\;n = 0,\\ {\rm{1,}}\;\;\;\;\;n{\rm{ = 1,}}...{\rm{ ,}}N{\rm{ - 1,}} \end{array} \right.$ | (9) |
where $f_0,...,f_{T-1}$ is a finite F0 contour of length $T$,and represented by $N$ coefficients,$c_0,...,c_{N-1}$. Similarly, the inverse DCT transformation (IDCT) is defined as
| \begin{align} &f_t=\sqrt 2 \sum_{n=0}^{N-1}\alpha_n c_n {\rm cos}\left\{ \frac{\pi}{T}n\left(t+\frac{1}{2}\right)\right \},\notag\\ &\qquad\qquad\qquad\qquad\qquad\qquad t=0,1,...,T-1. \end{align} | (10) |
The first coefficient of DCT is the mean of F0 contour and the rest are the weights for cosine functions with different frequencies. DCT has a strong energy compaction property,most of the signal information tends to be concentrated in a few low-frequency components of the DCT. In previous researches,5 DCT coefficients were used to represent a syllable F0 contour of neutral speech[16],and 8 DCT coefficients were used for emotional mandarin speech[17]. Considering that a syllable in singing voice is always longer than speech,and there also exists more dynamic[25],so more coefficients may be needed for singing voice. The number of DCT coefficients is discussed in Section V-D.
2) DCT-based syllable-level F0 model. In syllable level F0 model, sparseness of F0 is also a problem,so DCT is performing on residual F0 contour. Fig. 5 shows the procedure. Firstly,F0 of musical score is subtracted from F0 contour,and then the residual F0 contour is parameterized by DCT at syllable level. Fig. 6 shows basic shapes of syllable F0 contour.

|
Download:
|
| Fig. 5. Procedure of performing DCT on syllable level F0 contour. | |

|
Download:
|
| Fig. 6. Basic shapes of syllable F0 contour, K-means is performed on DCT coefficients, and then F0 contour is reconstructed from DCT coefficients of centroid of each cluster, C is the number of clusters. | |
During training,context-dependent HMMs $\pmb \lambda_s$ are trained for syllable DCTs,the same contextual factors with state level models are used for decision tree clustering.
C. Generation Integrating Two LevelsDuring generation,DF0 model and syllable-level DCT model are integrated to generate F0 contour[16],
| \begin{align} \hat{\pmb f} =\arg\max\limits_{\pmb f} P( W \pmb f|\pmb \lambda)P( D(\pmb f-\pmb f_{\rm score})|\pmb \lambda_s)^{\alpha}, \end{align} | (11) |
where $\pmb f$ is static F0 sequence,and $\pmb f_{\rm score}$ is F0 value of note sequence on musical score,$ D$ is the matrix for calculating DCT coefficients from F0 contour,structure of $ D$ is shown in (16),$\alpha$ is weight of syllable level model. Solving (11),the MLPG algorithm combined two level can be written as
| $\begin{array}{l} ({W^{\rm{T}}}{U^{ - 1}}W + \alpha {D^{\rm{T}}}U_s^{ - 1}D)\hat f\\ \qquad = {W^{\rm{T}}}{U^{ - 1}}{M^{F0}} + \alpha {D^{\rm{T}}}U_s^{ - 1}{M_s},{\Sigma _{s,{q_S}}}\} , \end{array}$ | (12) |
| \begin{align} \pmb U_s={\rm diag}\{ \Sigma_{s,q_1},..., \end{align} | (13) |
| \begin{align} \pmb M_s=[\pmb \mu_{s,q_1},...,\pmb \mu_{s,q_S}]^{\rm T} + D \pmb f_{\rm score}, \end{align} | (14) |
| \begin{align} D=\dfrac{\sqrt{2}}{T} \left(\begin{matrix} \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} &... & \dfrac{1}{\sqrt{2}} \\[4mm] {\cos}\left(\dfrac{\pi}{T}\left(\dfrac{1}{2}\right)\right) & {\cos}\left(\dfrac{\pi}{T}\left(1+\dfrac{1}{2}\right)\right) & ... &{\cos}\left(\dfrac{\pi}{T}\left(T-1+\dfrac{1}{2}\right)\right) \\[1mm] \vdots & \vdots & \ddots & \vdots \\[1mm] {\cos}\left(\dfrac{\pi}{T}(N-1)\left(\dfrac{1}{2}\right)\right) &{\cos}\left(\dfrac{\pi}{T}(N-1)\left(1+\dfrac{1}{2}\right)\right) &... & {\cos}\left(\dfrac{\pi}{T}(N-1)\left(T-1+\dfrac{1}{2}\right)\right)\\ \end{matrix} \right), \end{align} | (15) |
where $S$ is the number of syllable,$\pmb \mu_{s,q_s}$ and $ \Sigma_{s,q_s}$ are the mean vector and covariance matrix of the $q_s$-th syllable respectively. An informal listening test is conducted to decide the value of $\alpha$. At last,$\alpha$ is set to be $\frac{3.0T}{NS}$,which is $3.0$ times the ratio of the number of dimensions between $\pmb M$ and $\pmb M_s$.
Ⅴ. EXPERIMENTS A. Experimental ConditionsThe corpus presented in Section Ⅲ-A was used in our experiments. The database was randomly divided into two parts,training and testing sets. The total length of training set was $115$ minutes. And the total length of testing set was $17$ minutes.
34-order MGCs[29],35 parameters including energy component, were extracted from speech signals by performing spectral analysis with a 25 ms Hamming window,shifted every 5 ms. F0 was extracted by get_f0 method in Snack[30] without manual corrections. logF0 value was used for F0 feature. vibrato was extracted[24] and vibrato component was subtracted from F0 contour. After appending the dynamic features,the logF0,vibrato and MGC features consisting of static,velocity,and acceleration components.
7-state,left-to-right multi-stream hidden semi-Markov model (HSMM)[31] was used. The MGC stream was modeled with a single multivariate Gaussian distributions. The F0 stream and vibrato stream was modeled with multi-space probability distributions HSMM[18],a Gaussian distribution for voiced/vibrato frames and a discrete distribution for unvoiced/non-vibrato frames.
HTS Toolkit[32] was used to build the systems. A comparison of F0 generation method of baseline system and the proposed system is summarized in Table Ⅱ. Vibrato was modeled but not used at F0 generation in system baseline,DF0-A,DF0-B and DCT. The difference between DF0-A and DF0-B has been presented in Section IV-A. System VIB was the system DCT with vibrato component added. In all the systems,vibrato component was subtracted from F0 contour,and intonational component was used for F0 stream.
|
|
TABLE Ⅱ THE SYSTEMS USED IN EXPERIMENTS |
We used flat start uniformed labels to initially trained the baseline model,which was then used to do forced alignments on the training data to obtain syllable and state alignment. After that,timing model[7] was trained for precise rhythm. As described in Section IV,DF0 model was trained with the help of state alignment,and DCT parameterized syllable F0 model was also trained using 1-state HMM model with the help of syllable alignment. It should be noted that DCT was performed on intonation component of F0.
At synthesis stage,state duration was determined according to timing model and state duration model. And state duration were kept to be the same for all the systems in evaluation. The MLSA filter was used as synthesis filter.
B. Model StructureMinimum description length (MDL) criterion[19] was used as stopping criterion in decision growing. MDL factor was set to be $1$. Table Ⅲ shows the number of leaf nodes in the decision trees: state level spectrum,F0,vibrato and syllable level DCT models. The number of leaf nodes of F0 and MGC are similar with the result in Cheng's work[14]. The number of leaf nodes of F0 and DF0 is very near. The number of leaf nodes of state level models is larger than the result in Sinsy[9],because more training data was used in the proposed system and language was also different. There had been no syllable level DCT model for F0 in singing synthesis before. The number of leaf nodes is slightly smaller than that in mandarin Chinese speech synthesis[16], this is reasonable because residual F0 contour was modeled here.
|
|
TABLE Ⅲ NUMBER OF LEAF NODES IN THE SYSTEMS |
In addition to the root mean square error (RMSE) and correlation measurement of F0,which are commonly used in speech synthesis. We used another measurement based on the sense of music. In music theory,an interval is the difference between two pitches,and the standard system for comparing interval sizes is with cents. If one knows the frequencies a and b of two notes,the number of cents measuring the interval from a to b may be calculated by the following formula (similar to the definition of decibel):
| \begin{align} cent(b,a)=1200{\rm log}_2\left(\frac{f_b}{f_a}\right), \end{align} | (16) |
where $f_b$ and $f_a$ are frequency in Hz.
We define a measurement called mean note distance (MND) based on cent,
| \begin{align} MND [cent] = \frac{\sum\limits_q^Q ND(q)}{Q},\\[2mm] \end{align} | (17) |
| \begin{align} ND(q)[cent]= \frac{|\sum\limits_i cent(b_i,a_i)|}{I_q}, \end{align} | (18) |
where $Q$ is the number of notes,$ND(q)$ means the distance between the $q$-th note of two F0 contours,$I_q$ is the number of frames in the $q$-th note,$b_i$ and $a_i$ are the values (Hz) of the $i$-th point in the $q$-th note. MND is calculated on the unit of note,it can measure whether the two sequences of note are "in tune",so it can measure the distance of two F0 contours in the sense of music.
D. Number of DCT CoefficientsTo determine the number of DCT coefficients,intonation component was reconstructed from DCT coefficients and compared with the original intonation component. Fig. 7 shows RMSE,correlation and MND on the reconstructed F0 contour and original F0 contour. Because vibrato detection was not perfectly right,there still existed vibrato in the intonation component. The residual vibrato may influenced these measurements,e.g.,MND to be a little higher, because vibrato extent is about 10-100 cents. When the number of DCT coefficients goes to $10$,RMSE is rather small,correlation is $0.99$ and MND is nearly $5$,which is a twentieth of a semitone that is very hard to be distinguished by human,so we set the number of DCT coefficients to be $10$ in the rest of the experiments.

|
Download:
|
| Fig. 7. (a) RMSE, (b) correlation, and (c) MND as a function of number of DCT coefficients. | |
Subjective listening tests were conducted to evaluate the naturalness of the synthetic singing voice. Ten segments were randomly selected from the test set were used for the evaluation. Average length of these segments was 30 seconds. Examples of the test segments are available at http://202.38.64.10/shysian/singingsynthesis/index.html.
Two subjective listening tests were conducted with a web-base interface. The first listening test was to evaluate the naturalness of the systems. Eight subjects were asked to rate the naturalness of the synthetic singing voice on a mean opinion score (MOS) with a scale from 1 (poor) to 5 (good). All the segments were in random order. Fig. 8 shows that the proposed systems significantly outperform the baseline system. This is because whether the synthetic F0 contour is "in tune" has a great impact on the subjective quality. The proposed systems can generate an "in tune" F0 contour,while the baseline system cannot because of data sparseness problem. DF0-A method is better than DF0-B method. That is maybe because DF0-A method generates DF0 from the same state sequence with other parameters (spectrum,vibrato),while DF0-B method generates DF0 from a different state sequence with other parameters. So in all of our experiments,DF0-A was used as state-level model for DCT method. DCT method is better than DF0-A method. According to our observation,DCT method generates more expressive F0 contour. We also see that the addition of vibrato slightly increase the naturalness. In the system,vibrato was generated at frame level,it is relation to note is ignored. Although vibrato can increase the expressiveness,sometimes the generated vibrato is a little unnatural,that is why subjects did not give a significantly higher score to system VIB compared with system DCT.

|
Download:
|
| Fig. 8. Mean opinion score of the baseline and the proposed systems, the confidence interval is 0:95. | |
The second listening test was an AB preference test to compare the expressiveness among the proposed systems. Eight subjects were asked to select from three preference choices: 1) the former is better (more expressive); 2) the latter is better; 3) no preference. All the segments were in random order. Fig. 9 shows that The syllable DCT model generated more expressive F0 contour than DF0-A method. And the addition of vibrato furtherly improved the expressiveness.

|
Download:
|
| Fig. 9. Results of AB preference test for expressiveness evaluation, NOP means no preference. | |
Table Ⅳ shows comparison of the objective measurements calculated on the test set for the baseline system and the proposed system. These measurements were calculated between the original F0 contour (intonation component) in the test set and the generated F0 contour (intonation component). The results show that the proposed methods outperform the baseline method in all the three measurements.
|
|
TABLE Ⅳ COMPARISON OF OBJECTIVE MEASUREMENTS |
Fig. 10 shows the synthesized F0 contour of a melisma,a single syllable $a$ ranging over three different notes (MIDI NOTEs: 62,60, 59). The solid line indicates the F0 contour of musical score,and the broken lines indicate the F0 contour generated by the proposed method and baseline method. Both two proposed methods generated better F0 contours than the baseline method. F0 value was converted to MIDI note by (20).

|
Download:
|
| Fig. 10. Synthesized F0 contour of a melisma, a single syllable a ranging over three different notes (MIDI NOTEs: 62, 60, 59), F0 value was converted to MIDI note. The solid line indicates the F0 contour of musical score, and the broken lines indicate the F0 contour generated by the proposed method and baseline method. | |
Fig. 11 shows a comparison of F0 contours generated by the baseline system and the proposed system. The F0 value was converted to MIDI note. The solid line indicates the F0 contour of musical score,and the broken lines indicate the F0 contour generated by the proposed method and baseline method. The two F0 contours generated by the proposed methods (DF0-A and syllable DCT) is "in tune" with the musical score,while the one generated by the baseline method is "out of tune" at some musical notes. Both DF0 and syllable DCT method can alleviate the data sparse problem to generate an "in tune" F0 contour. The syllable DCT method also generated a more expressive F0 contour than state DF0. Especially,preparation and overshoot of F0,which is observed during note transition[25], was successfully synthesized by the syllable DCT method.

|
Download:
|
| Fig. 11. F0 contour of synthetic singing voice compared with that of musical score, F0 value was converted to MIDI note. The solid line indicates the F0 contour of musical score, and the broken lines indicate the F0 contour generated by the proposed method and baseline method. | |
Fig. 12 shows an example of generated F0 contour with or without vibrato component. System VIB successfully generated a time-variant vibrato,which looks like an almost sinusoidal modulation.

|
Download:
|
| Fig. 12. An example of generated F0 contour with or without vibrato component. F0 value was in log value. The solid line indicates the F0 contour of musical score, and the broken lines indicate the generated F0 contour with or without vibratod. | |
As can be seen from Figs. 10-12,the generated F0 was a little lower than the musical score,this is because the singer had a tendency to sing a little flat. The same phenomenon has been observed in Sinsy[7].
Table Ⅴ shows statistics of variance of generated F0 in system DF0-A and DCT. We can see that variance of F0 was larger in system DCT than in system DF0-A. Over-smoothness was partly compensated by integrating statistical models of two levels.
|
|
TABLE Ⅴ VARIANCE OF GENERATED F0 |
Our DF0-A method is a special form of pitch adaptive training method,it only perform a single Viterbi alignment,and then difference between F0 and musical score is modeled. By doing this, it can handle the situation of melisma. It also benefits from not doing pitch normalization before training,So that DF0 and other parameters (spectrum,vibrato and etc) can be estimated and generated with the same state sequence (synchronous state). DF0-B method is actually very similar with data-level pitch normalization method,the difference is that DF0 data is obtained through a more accurate alignment. In DF0-B method,DF0 model parameter is estimated and DF0 parameter is generated from different state sequences (asynchronous state) with other acoustic parameters.
Ⅶ. CONCLUSIONWe have proposed a HMM-based mandarin Chinese singing voice synthesis system. A mandarin Chinese singing voice corpus was recorded and musical contextual features were well designed for training. We solve the data sparse problem and handle the situation of melisma at the same time inside the HMM-based framework. Discrete cosine transform (DCT) F0 model is also apllied,and two level statistical models are integrated for generation to overcome over-smoothing of generated F0 contour. Objective and subjective evaluations showed that our system can generate a natural and "in tune" F0 contour. Furthermore,the method integrating two level statistical models successfully made singing voice more expressive.
As we can see from experimental results,modeling of vibrato can improve the naturalness and expressiveness of the singing voice. In this paper,vibrato was generated at state level,its relation to the note was not explicitly considered. Future work will focus on modeling vibrato by considering its relation to note explicitly.
The quality of the synthetic voice is expected to rise if better spectrum extraction method is used. So another future work is using better spectrum estimator to substitute the conventional mel-cepstral analysis.
| [1] | Cook P R. Singing voice synthesis: history, current work, and future directions. Computer Music Journal, 1996, 20(3): 38-46 |
| [2] | Bonada J, Serra X. Synthesis of the singing voice by performance sampling and spectral models. IEEE Signal Processing Magazine, 2007, 24(2): 69-79 |
| [3] | Bonada J. Voice Processing and Synthesis by Performance Sampling and Spectral Models [Ph. D. dissertation], Universitat Pompeu Fabra, Barcelona, 2008. |
| [4] | Kenmochi H, Ohshita H. VOCALOID-commercial singing synthesizer based on sample concatenation. In: Proceedings of the 8th Annual Conference of the International Speech Communication Association. Antwerp, Belgium, 2007. 4009-4010 |
| [5] | Ling Z H, Wu Y J, Wang Y P, Qin L, Wang R H. USTC system for blizzard challenge 2006 an improved HMM-based speech synthesis method. In: Blizzard Challenge Workshop. Pittsburgh, USA, 2006. |
| [6] | Zen H G, Tokuda K, Black A W. Statistical parametric speech synthesis. Speech Communication, 2009, 51(11): 1039-1064 |
| [7] | Saino K, Zen H G, Nankaku Y, Lee A, Tokuda K. An HMM-based singing voice synthesis system. In: Proceedings of the 9th International Conference on Spoken Language Processing. Pittsburgh, PA, USA, 2006. |
| [8] | Mase A, Oura K, Nankaku Y, Tokuda K. HMM-based singing voice synthesis system using pitch-shifted pseudo training data. In: Proceedings of the 11th Annual Conference of the International Speech Communication Association. Makuhari, Chiba, Japan, 2010. 845-848 |
| [9] | Oura K, Mase A, Yamada T, Muto S, Nankaku Y, Tokuda K. Recent development of the HMM-based singing voice synthesis system - Sinsy. In: Proceedings of the 2010 ICASSP. Kyoto, Japan, 2010. 211 -216 |
| [10] | Oura K, Mase A, Nankaku Y, Tokuda K. Pitch adaptive training for HMM-based singing voice synthesis. In: Proceedings of the 2012 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). Kyoto: IEEE, 2012. 5377-5380 |
| [11] | Zhou S S, Chen Q C, Wang D D, Yang X H. A corpus-based concatenative mandarin singing voice synthesis system. In: Proceedings of the 2008 International Conference on Machine Learning and Cybernetics. Kunming, China: IEEE, 2008. 2695-2699 |
| [12] | Li J L, Yang H W, Zhang W Z, Cai L H. A lyrics to singing voice synthesis system with variable timbre. In: Proceedings of the 2011 International Conference, Applied Informatics, and Communication. Xi'an, China: Springer, 2011. 186-193 |
| [13] | Gu H Y, Liau H L. Mandarin singing voice synthesis using an HNM based scheme. In: Proceedings of the 2008 Congress on Image and Signal Processing. Sanya, China: IEEE, 2008. 347-351 |
| [14] | Cheng J Y, Huang Y C, Wu C H. HMM-based mandarin singing voice synthesis using tailored synthesis units and question sets. Computational Linguistics and Chinese Language Processing, 2013, 18(4): 63-80 |
| [15] | Latorre J, Akamine M. Multilevel parametric-base F0 model for speech synthesis. In: Proceedings of the 9th Annual Conference of the International Speech Communication Association. Brisbane, Australia, 2008. 2274-2277 |
| [16] | Qian Y, Wu Z Z, Gao B Y, Soong F K. Improved prosody generation by maximizing joint probability of state and longer units. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(6): 1702-1710 |
| [17] | Li X, Yu J, Wang Z F. Prosody conversion for mandarin emotional voice conversion. Acta Acustica, 2014, 39(4): 509-516 (in Chinese) |
| [18] | Tokuda K, Masuko T, Miyazaki N, Kobayashi T. Hidden Markov models based on multi-space probability distribution for pitch pattern modeling. In: Proceedings of the 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing. Phoenix, AZ: IEEE, 1999. 229-232 |
| [19] | Shinoda K, Watanabe T. MDL-based context-dependent subword modeling for speech recognition. The Journal of the Acoustical Society of Japan (E), 2000, 21(2): 79-86 |
| [20] | Tokuda K, Yoshimura T, Masuko T, Kobayashi T, Kitamura T. Speech parameter generation algorithms for HMM-based speech synthesis. In: Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing. Istanbul: IEEE, 2000. 1315-1318 |
| [21] | Imai S, Sumita K, Furuichi C. Mel log spectrum approximation (MLSA) filter for speech synthesis. Electronics and Communications in Japan (Part I: Communications), 1983, 66(2): 10-18 |
| [22] | Saino K, Tachibana M, Kenmochi H. An HMM-based singing style modeling system for singing voice synthesizers. In: Proceedings of the 7th ISCA Workshop on Speech Synthesis, 2010. |
| [23] | Yamagishi J, Kobayashi T. Average-voice-based speech synthesis using HSMM-based speaker adaptation and adaptive training. IEICETransactions on Information and Systems, 2007, E90-D(2): 533-543 |
| [24] | Nakano T, Goto M. An automatic singing skill evaluation method for unknown melodies using pitch interval accuracy and vibrato features. In: Proceedings of the 9th International Conference on Spoken Language Processing. Pittsburgh, PA, USA, 2006. 1706-1709 |
| [25] | Saitou T, Unoki M, Akagi M. Development of an F0 control model based on F0 dynamic characteristics for singing-voice synthesis. Speech Communication, 2005, 46(3-4): 405-417 |
| [26] | LilyPond [Online], available: http://lilypond.org/. 2015. |
| [27] | Devaney J C, Mandel M I, Fujinaga I. Characterizing singing voice fundamental frequency trajectories. In: Proceedings of the 2011 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. New Paltz, NY: IEEE, 2011.73-76 |
| [28] | Lee S W, Dong M H, Li H Z. A study of F0 modelling and generation with lyrics and shape characterization for singing voice synthesis. In: Proceedings of the 8th International Symposium on Chinese Spoken Language Processing. Kowloon: IEEE, 2012. 150-154 |
| [29] | Koishida K, Tokuda K, Kobayashi T, Imai S. CELP coding based on melcepstral analysis. In: Proceedings of the 1995 International Conference on Acoustics, Speech, and Signal Processing. Detroit, MI: IEEE, 1995. 33-36 |
| [30] | Snack [Online], available: http://www.speech.kth.se/snack/. 2015. |
| [31] | Zen H G, Tokuda K, Masuko T, Kobayashi T, Kitamura T. Hidden semi-Markov model based speech synthesis. In: Proceedings of the 8th International Conference on Spoken Language Processing. Jeju Island, Korea, 2004. 1-4 |
| [32] | HMM-based speech synthesis system (HTS) [Online], available: http://hts.sp.nitech.ac.jp. 2015. |
 2016, Vol.3
2016, Vol.3 


