2. School of Mathematics and Information, South China Agricultural University, Guangzhou 510640, China
THE very first notion of fractional calculus,that deals with derivatives and integrals of non-integer orders (including complex orders),is believed to be a question raised in the year 1695 by L'Hôspital in a letter addressed to Leibniz, which was seeking the meaning of the derivative of half order. The applications of fractional calculus to physics and engineering,just recently attracted interest[1, 2]. Although,it is developed as a field of applied mathematics with a history of more than three centuries old. There is an increase in the list of applications of fractional calculus and comprises of viscoelastic materials and rheology,electrical engineering,electrochemistry,biology, biophysics and bioengineering,signal and image processing, mechatronics,and control theory[3].
Poincaré-Bendixson theorem[4] states that,chaos can only arise in a continuous autonomous dynamical system (represented by a differential equation or set of differential equations) if it has three or more dimensions. However,over the last few years,it has been revealed that chaos[5, 6, 7, 8, 9] and hyperchaos[10, 11] exist in fractional-order systems. In a seminal letter[6],the effective dimension of such systems was denoted by $\Sigma$. Moreover,the minimum effective dimension $\Sigma_{cr}$ was defined as a certain critical value,under which the system exhibits periodic dynamics. Thus one gratifying work is to determine the minimum effective dimension $\Sigma_{cr}$ for a given fractional-order system. Note that a chaotic system is referred to be extremely sensitive to its initial conditions,and the ``memory'' time of the system can be estimated as $t_{\rm mem}=\lambda_{\rm max}^{-1}$,where $\lambda_{\rm max}$ is the largest Lyapunov exponent,which is obtained through numerical computations. Generally,a positive maximal Lyapunov exponent is commonly taken as an indication that the system is chaotic. On the other hand, consider a 3-D nonlinear dynamical system $\dot x=f(x),\ x \in {\bf R}^3$,and $x_e$ is an equilibrium point,then $x_e$ is called a saddle-focus if the eigenvalues of the Jacobian $A = Df$ evaluated at $x_e$ are $\lambda_1=\mu,~\lambda_{2,3}=\sigma \pm i \omega,$ and satisfy $\mu\sigma<0,\omega\neq 0$,where $\mu,\sigma,\omega \in {\bf R}$. Also,$x_e$ is called a node-focus if the eigenvalues of the Jacobian $A = Df$ evaluated at $x_e$ are $\lambda_1=\mu,~\lambda_{2,3}=\sigma \pm i \omega,$ and satisfy $\mu\sigma>0,\omega\neq 0$. Note that many fractional-order systems[6, 7, 8, 9, 10] and their references display chaotic dynamics with one saddle and two saddle-foci,while in [12] a Lorenz-like fractional order chaotic system is introduced with one saddle and two stable node-foci. However,this paper proposes a new fractional-order system with only two stable node-foci. It is crystal clear that the system will be topologically non-equivalent to the original fractional-order Lorenz and all Lorenz-like systems. Therefore,what is interesting is to further find out what kind of new dynamics this system has.
The paper is organized as follows. In Section Ⅱ,basic definitions of fractional calculus as well as some useful theorems of stability of fractional-order systems are briefly introduced. Section Ⅲ is dedicated to the local stability and chaotic dynamics of the new fractional-order Lorenz-like system. In Section Ⅳ,the combination synchronization of this system with two other systems is analyzed. Conclusions are drawn in Section Ⅴ.
Ⅱ. PRELIMINARIES A. Basic DefinitionsThere are several definitions of fractional derivatives[13]. Two most commonly used definitions are Riemann-Liouville and Caputo definitions.
Definition 1. Let $m-1< \delta< m$,$m \in {\bf N}$,the Riemann-Liouville fractional derivative of order $\delta$ of any function $f(t)$ is defined as follows
| $ D_t^\delta f(t) = \frac{1}{{\Gamma (m - \delta)}}\frac{{{{\rm d}^m}}}{{{\rm d}{t^m}}}{\int_0^t {\left( {t - \tau } \right)} ^{m - \delta - 1}}f\left( \tau \right){\rm d}\tau. $ | (1) |
Definition 2. Let $f \in C_{-1}^{m}$,$m \in {\bf N}$,the Caputo fractional derivative of $f(t)$ is defined by
| $ D_t^{\alpha} f(t) = \frac{1}{\Gamma(m-\alpha)} \int_{0}^{t}{(t-\tau)}^{m-\alpha-1} \frac{{\rm d}^{m} f(\tau)}{{\rm d} \tau^{m}} {\rm d}\tau. $ | (2) |
The advantage of Caputo approach is that the initial conditions for fractional order differential equations with Caputo derivatives take on the same form as for integer-order differential equations,whereas the case is not the same for the Riemann-Liouville derivative. Therefore,in the rest of this paper,the notation $D_{t}^{\alpha}$ is taken as the Caputo fractional derivative.
B. Stability LemmasIn this subsection,stability lemmas on fractional-order systems are introduced. The first lemma is given for fractional order linear systems,while the second and third for nonlinear system, commensurate and incommensurate case,respectively.
Lemma 1[15]. The following autonomous system:
| $ D_{t}^{\alpha}x=Ax,\quad x(0)=x_0, $ | (3) |
with $0<\alpha \leq 1$,$x \in {\bf R}^n$,and $A \in {\bf R}^{n \times n}$,is asymptotically stable if and only if $|\arg(\lambda)|> \alpha \pi /2$ is satisfied for all eigenvalues of matrix $A$. Also,this system is stable if and only if $|\arg(\lambda)| \ge \alpha \pi /2$ is satisfied for all eigenvalues of matrix $A$ with those critical eigenvalues satisfying $|\arg(\lambda)|= \alpha \pi /2$ having geometric multiplicity of one. The geometric multiplicity of an eigenvalue $\lambda$ of the matrix $A$ is the dimension of the subspace of vectors $v$ for which $Av=\lambda v$.
Lemma 2[16]. Consider the following commensurate fractional order system:
| $ D_{t}^{\alpha}x=f(x), $ | (4) |
where $0<\alpha \leq 1$ and $x \in {\bf R}^n$. The equilibrium points are calculated by solving the following equation: $f (x) = 0$. These points are locally asymptotically stable if all eigenvalues $\lambda_i$ of the Jacobian matrix $J=\frac{\partial f}{ \partial x}$ evaluated at the equilibrium points satisfy: $|\arg(\lambda_i)|> \alpha \pi /2$.
Lemma 3[17]. If the origin $O$ is a hyperbolic equilibrium point of (4),then vector field $f(x)$ is topologically equivalent with its linearized vector field $Df(0)_x$ in the neighbourhood $\delta(0)$ of the origin $O$.
Lemma 4[18]. The following is a linear incommensurate fractional order system:
| $ D_{t}^{\alpha}x=Ax,\quad x(0)=x_0, $ | (5) |
where $\alpha=(\alpha_1,\alpha_2,\ldots,\alpha_n),0<\alpha_i<1, i=1,2,\ldots,n$ and $x \in {\bf R}^n$. Suppose that $\alpha_i$'s are rational numbers between $0$ and $1$. Let $\gamma=1/m$ is the least common multiple of the denominators $m_i$ of $\alpha_i$'s where $\alpha_i=k_i/m_i,k_i,m_i\in {\bf N}$. Then the system (5) is asymptotically stable if all roots $\lambda$ of the equation ${\rm det}({\rm diag}(\lambda^{m\alpha_1},\lambda^{m\alpha_2},\ldots, \lambda^{m\alpha_n})-A)=0$ satisfy $|{\rm arg}(\lambda)|>\gamma \pi/2$.
Lemma 5[19]. Given the polynomial,
| $ P(\lambda)=\lambda^n + a_1\lambda^{n-1} + \cdots +a_{n-1}\lambda + a_n, $ | (6) |
where the coefficients $a_i$ are real constants,$i = 1,\ldots,n$, define the n Hurwitz matrices using the coefficients $a_i$ of the characteristic polynomial:
$$ \begin{equation*} \Delta_1 = a_1,\ \Delta_2 = \left( {\begin{array}{*{20}{c}} a_1 & 1 \\ a_3 & a_2 \\ \end{array}} \right),\\ \end{equation*} $$and
$$ \begin{equation*} \Delta_3 = \left( {\begin{array}{*{20}{c}} a_1 & 1 & 0 \\ a_3 & a_2 & {a_1} \\ {a_5} & {a_4} & {a_3} \\ \end{array}} \right), \end{equation*} $$where $a_j=0$ if $j > n$. All of the roots of the polynomial $P(\lambda)$ have negative real part if and only if the determinants of all Hurwitz matrices are positive:
$$ \begin{equation*} {\rm det}\Delta_j > 0, j=1,2,\ldots,n, \end{equation*} $$when $n=3$,the Routh-Hurwitz criteria simplify to $\Delta_1>0$, $\Delta_2>0$ and $\Delta_3=a_1a_2>a_3$,if the condition $\Delta_2$ holds,then (6) has three roots with negative real parts.
In the other case,if the condition $\Delta_2<0$ holds,(6) has one pair of complex conjugate eigenvalues with positive real parts,along with one negative real eigenvalue.
Ⅲ. FRACTIONAL-ORDER LORENZ-LIKE SYSTEM A. Local StabilityThe integer-order Lorenz-like system[14] is
| $ \left\{ \begin{array}{l} \frac{{{\rm d}x}}{{{\rm d}t}} = a(y - x) ,\\ \frac{{{\rm d}y}}{{{\rm d}t}} = -cy - xz ,\\ \frac{{{\rm d}z}}{{{\rm d}t}} = xy - b , \end{array} \right. $ | (7) |
where $a>0$,$b>0$,and $c>0$. A more complex local analysis and the existence of homoclinic and heteroclinic orbits of system (7) has been studied in [14] thoroughly. In order to study the effect of fractional derivatives,then the corresponding fractional-order Lorenz-like system can be stated in the form
| $ \left\{ \begin{array}{l} D_{t}^{\alpha}x = a(y - x) ,\\ D_{t}^{\alpha}y = -cy - xz ,\\ D_{t}^{\alpha}z = xy -b, \end{array} \right. $ | (8) |
where $a>0$,$b>0$,$c>0$,and $0<\alpha \leq 1$. When $\alpha=\alpha_1=\alpha_2=\alpha_3$ the case is known as the commensurate,and when $\alpha_i$ $(i=1,2,3)$ are not all equal, it is known as incommensurate case.
Note that system (8) (thus its solution) is invariant under the transformation $T(x,y,z)\rightarrow (-x,-y,z)$. This means that any orbit that is not itself invariant under $T$ must have its "twin" orbit in the sense of this transformation. Further,in the system (8),there are two equilibria:
| $ {E^ \pm } = (\pm \sqrt{b},\pm \sqrt{b},-c). $ | (9) |
System (8) is linearized about the equilibria ${E^{\pm}}$, yielding the Jacobian matrix
| $ DF|_{E^{\pm}} = \left( {\begin{array}{*{20}{c}} -a & { a} & 0 \\ c & -c & \mp \sqrt{b} \\ \pm \sqrt{b} & \pm \sqrt{b} & {0} \\ \end{array}} \right), $ | (10) |
and characteristic equation is given by
| $ \lambda^3+\left(a+c\right)\lambda^2+b\lambda+2 a b=0. $ | (11) |
Further,calculating the Routh-Hurwitz determinants
| $ \begin{array}{lll} \Delta_1=a+c>0,\\ \Delta_2=\left| {\begin{array}{*{20}{c}} {a+c} & { 1} \\ 2 a b & b \\ \end{array}} \right|,\\ \Delta_3=\left| {\begin{array}{*{20}{c}} {a+c} & { 1} & 0\\ 2a b & {b} & a+c\\ 0 & {0} & 2ab\\ \end{array}} \right|=2ab\Delta_2. \end{array} $ | (12) |
According to Lemma 5,if condition
| $ \Delta_2>0, {\rm i.e.},b(c-a)>0 $ | (13) |
holds,then the characteristic equation (11) has three roots with negative real parts.
In other case,if the condition
| $ \Delta_2<0, {\rm i.e.},b(c-a)<0 $ | (14) |
holds,then the characteristic equation (11) has one pair of complex conjugate eigenvalues with positive real parts,along with one negative real eigenvalue.
Suppose that ${\lambda _1}<0$ and ${\lambda _{2,3}} = \beta \pm \gamma i ~( \beta >0)$ are the eigenvalues of characteristic polynomial (11),thus
| $ \left( {\lambda - {\lambda _1}} \right)\left( {\lambda - \beta - \gamma i} \right)\left( {\lambda - \beta + \gamma i} \right) = 0, $ | (15) |
or equivalently
| $ \lambda^{3}-(2\beta + {\lambda _1}) \lambda^{2}+(2\beta \lambda_1 + {\beta ^2} + {\gamma ^2})\lambda-\lambda_1 ({\beta ^2} + {\gamma ^2}). $ | (16) |
By comparing (11) and (16),we get
| $ \left\{\begin{array}{l} a+c = - 2\beta - {\lambda _1},\\ b = 2\beta \lambda_1 + {\beta ^2} + {\gamma ^2},\\ 2ab=-\lambda_1 ({\beta ^2} + {\gamma ^2}). \end{array} \right. $ | (17) |
From the first equation of (17),we have
| $ \beta=-\frac{a+c+\lambda_1}{2}. $ | (18) |
Further,by multiplying both sides of the third equation of (17) by $1/\beta^2$,it follows that
| $ \frac{2ab}{\beta^2}=-\lambda_1(1+(\frac{\gamma}{\beta})^2), $ | (19) |
which implies
| $ (\frac{\gamma}{\beta})^2=\frac{2ab}{-\lambda_1 \beta^2}-1. $ | (20) |
Substituting (18) into the right side of (20),gives that
| $ (\frac{\gamma}{\beta})^2=\frac{8ab}{-\lambda_1 (a+c+\lambda_1)^2}-1. $ | (21) |
Hence
| $ \begin{array}{ll} {|\arg ({\lambda _{2,3}})|} &= \arctan (\frac{\gamma}{\beta})=\arctan \Big( \sqrt{ \frac{8ab }{-\lambda_1(a+c+\lambda_1)^2}-1}\Big). \end{array} $ | (22) |
Then according to above discussions,we have the following theorem of commensurate case.
Theorem 1. Suppose that $a>0$,$b>0$ and $c>0$ in system (8),then equilibria ${E^ + }$ and ${E^ - }$ are all asymptotically stable if $\left( {a,b,c} \right) \in {\Omega_1}\cup {\Omega_2}$,where
$${\Omega_1} = \Big\{ ( {a,b,c}) \Big| a > 0,b > 0,c>a\Big\},$$ $$\begin{array}{lll} {\Omega_2} = \Big\{ ( {a,b,c}) \Big| a > 0,b > 0,|c|<a,\\ \qquad \ \ ~ \arctan \Big( \sqrt{ \frac{8ab }{-\lambda_1(a+c+\lambda_1)^2}-1} \ \ \Big)>\frac{{{\alpha} \pi} }{{2}} \Big\}. \end{array}$$Proof. For the equilibria ${E^ + }$ and ${E^ - }$,there are two cases of Routh-Hurwitz determinants. In the first case,i.e., condition (13) is satisfied,then equilibria ${E^{\pm} }$ are all asymptotically stable since the characteristic equation (11) has three roots with negative real parts. In the second case,i.e., condition (16) is satisfied,then we have,from (22) and Lemma 2, that equilibria ${E^{\pm} }$ are all asymptotically stable if $\arctan \Big( \sqrt{ \frac{8abc }{-\lambda_1(a+b+\lambda_1)^2}-1} \ \ \Big)>{{\alpha} \pi }/{2}$. Therefore,equilibria ${E^ + }$ and ${E^ - }$ are all asymptotically stable if $\left( {a,b,c} \right) \in {\Omega_1}\cup {\Omega_2}$.
B. Numerical AlgorithmThere exist numerous traditional methods to deal with the numerical computations of fractional-order differential equations: 1) Using standard integer operators,approximating fractional operators obtained by utilizing frequency domain techniques based on Bode diagrams[5]; 2) By linearizing the nonlinear fractional differential equation at every step of integration and iteratively applying the analytical expression of the solution of linearized fractional differential equation[6]; 3) deriving the expression analytically of the solution of the nonlinear fractional differential equation and iterating the formula numerically by using generalized Admas-Bashforth-Moulton scheme[20]; 4) Additional analytical methods[21, 22, 23]. Among the above forementioned methods,the third one is at least super-linearly convergent and has a better numerical stability,especially it possesses the inherent characteristic,"memory effects",of fractional derivatives. A good amount of comprehensive discussion of the above techniques has been presented in the literature[24, 25].
Utilizing the scheme of generalized Admas-Bashforth-Moulton[20],the numerical scheme for fractional-order Lorenz-like system (8) is derived. Set $h=N/T$, $t_n=nh,~n=1,2,\ldots,N \in {\bf Z}^{+}$,the fractional-order Lorenz-like system (8) can be discretized as
$$ \left\{ \begin{array}{l} {x_h}\left( {{t_{n + 1}}} \right) = {x_0} + \frac{{{h^\alpha}}}{{\Gamma \left( {\alpha + 2} \right)}}\left( {a\left( {{y^p}\left( {{t_{n + 1}}} \right) - {x^p}\left( {{t_{n + 1}}} \right)} \right)} \right) \\ \qquad\qquad\quad + \frac{{{h^\alpha}}}{{\Gamma \left( {\alpha + 2} \right)}}\sum\limits_{j = 0}^n {{\alpha_{j,n + 1}}\left( {a\left( {y\left( {{t_j}} \right) - x\left( {{t_j}} \right)} \right)} \right)} ,\\ {y_h}\left( {{t_{n + 1}}} \right) = {y_0} + \frac{{{h^\alpha}}}{{\Gamma \left( {\alpha + 2} \right)}}\left( {-c{y^p}\left( {{t_{n + 1}}} \right) - {x^p}\left( {{t_{n + 1}}} \right){z^p}\left( {{t_{n + 1}}} \right)} \right) \\ \qquad\qquad\quad + \frac{{{h^\alpha}}}{{\Gamma \left( {\alpha + 2} \right)}}\sum\limits_{j = 0}^n {{\alpha_{j,n + 1}}\left( {-cy\left( {{t_j}} \right) - x\left( {{t_j}} \right)z\left( {{t_j}} \right)} \right)} ,\\ {z_h}\left( {{t_{n + 1}}} \right) = {z_0} + \frac{{{h^\alpha}}}{{\Gamma \left( {\alpha + 2} \right)}}\left( {{x^p}\left( {{t_{n + 1}}} \right){y^p}\left( {{t_{n + 1}}} \right) - b} \right) \\ \qquad\qquad\quad + \frac{{{h^\alpha}}}{{\Gamma \left( {\alpha + 2} \right)}}\sum\limits_{j = 0}^n {{\alpha_{j,n + 1}}\left( {x\left( {{t_j}} \right)y\left( {{t_j}} \right) - b} \right)} ,\\ \end{array} \right. $$in which
$$ \left\{ \begin{array}{l} {x^p}\left( {{t_{n + 1}}} \right) = {x_0} + \frac{1}{{\Gamma \left( \alpha \right)}}\sum\limits_{j = 0}^n {{\beta_{j,n + 1}}\left( {a\left( {y\left( {{t_j}} \right) - x\left( {{t_j}} \right)} \right)} \right)} ,\\ {y^p}\left( {{t_{n + 1}}} \right) = {y_0} + \frac{1}{{\Gamma \left( \alpha \right)}}\sum\limits_{j = 0}^n {{\beta_{j,n + 1}}\left( {-cy\left( {{t_j}} \right) - x\left( {{t_j}} \right)z\left( {{t_j}} \right)} \right)} ,\\ {z^p}\left( {{t_{n + 1}}} \right) = {z_0} + \frac{1}{{\Gamma \left( \alpha \right)}}\sum\limits_{j = 0}^n {{\beta_{j,n + 1}}\left( {x\left( {{t_j}} \right)y\left( {{t_j}} \right) - b} \right)} ,\\ \end{array} \right. $$ $$ \alpha_{j,n + 1}=\left\{ \begin{array}{ll} {n^{\alpha + 1}} - \left( {n - \alpha} \right){\left( {n + 1} \right)^\alpha},& j = 0,\\ {\left( {n - j + 2} \right)^{\alpha + 1}} + {\left( {n - j} \right)^{\alpha + 1}} \\ - 2{\left( {n - j + 1} \right)^{\alpha + 1}},& 1 \le j \le n,\\ 1,& j = n + 1,\end{array}\right. $$ $$ {\beta_{j,n + 1}} = \frac{{{h^\alpha}}}{\alpha}\left( {{{\left( {n + 1 - j} \right)}^\alpha} - {{\left( {n - j} \right)}^\alpha}} \right),\ \ 0 \le j \le n. $$The discretization process of incommensurate case can easily be followed similarly as the above commensurate case.
C. Chaos VerificationGenerally,it is not easy to specify chaotic parametric regions analytically (including fractional order region) for a fractional order system. Lyapunov exponent is considered as the most handy numerical assessment for finding the "chaotic" properties of a dynamical system,which characterizes the extent of the sensitivity to initial conditions. More precisely,a positive maximal Lyapunov exponent is normally considered as a sign that the system is chaotic. Wolf[26] and Jacobian[27] algorithms are the most common algorithms for computing the maximal Lyapunov exponent of integer-order system. However,Jacobian algorithm is inapplicable for calculating maximal Lyapunov exponent of a fractional-order system,since the Jacobian matrix of fractional-order system is comparatively difficult to be obtained. As to Wolf algorithm,it is relatively hard to implement. Therefore,in this paper the maximal Lyapunov exponent is calculated from the small data sets[28].
Set the system parameters $(a,b,c)=(10,100,11.2)$,whilst vary the order $\alpha$ of the system to examine the fractional-order Lorenz-like system. By taking the initial value as $(x_0,y_0,z_0)=(0.98,-1.82,-0.49)$,step-length as $h=0.005$, iteration time as $N=10 000$,and omitting the first $2000$ data points,we find that the fractional-order Lorenz-like system is chaotic with the effective dimension $\Sigma<3$ since the corresponding maximal Lyapunov exponent is positive. For example, when $\alpha=0.9999$,this system exhibits double-scroll attractor, shown in Fig. 1.

|
Download:
|
| Fig. 1. Chaotic attractor of fractional-order Lorenz-like system (8) with parameters $(a,b,c,\alpha)=(10, 100, 11.2,0.9999)$ and the effective dimension $\Sigma=2.9997$. | |
In this case,the maximal Lyapunov exponent can be estimated as $\lambda_{\rm max} \approx 0.6017$. Note that for the common Lorenz-like system $\lambda_{\rm max} \approx 0.83296$[14]. This implies that decreasing of the effective dimension $\Sigma$ induces some effective damping in the fractional-order system,which is also true for fractional-order Lorenz system[16].
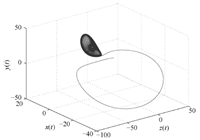
Further,by decreasing the order $\alpha$,it is found that this system cannot be chaotic when $\alpha\leq 0.9949$. In the case, the dynamical portrait of this system is shown in Fig. 2,from which the system is attracted by one of the two stable node-foci $E^{+}$ and $E^{-}$.
|
Download:
|
| Fig. 2. Stable node-foci of fractional-order Lorenz-like system (8) with parameters $(a,b,c,\alpha)=(10,100,11.2,0.9949)$ and the effective dimension $\Sigma=2.9847$. | |
In order to get the minimum effective dimension $\Sigma_{cr}$,the fractional order $\alpha$ is reset to $\alpha_1,\alpha_2, \alpha_3$ for each equation in system (8). In this case,system (8) is described as follows:
| $ \left\{ \begin{array}{l} D_{t}^{\alpha_1}x = a(y - x) ,\\ D_{t}^{\alpha_2}y = -cy - xz ,\\ D_{t}^{\alpha_3}z = - b+xy. \end{array} \right. $ | (23) |
Taking $\alpha_2=\alpha_3=1$,whilst reducing $\alpha_1$ from 1,the fractional-order Lorenz-like system remains chaotic until $\alpha_1=0.8485$. Also,taking $\alpha_1=\alpha_3=1$,whilst varying $\alpha_2$,the fractional-order Lorenz-like system behaves chaotically when $0.9900 \le \alpha_2 \le 1$ and does not display chaos if $\alpha_2$ continues to diminish. Furthermore,taking $\alpha_1=\alpha_2=1$,whilst reducing $\alpha_3$ from 1,similar phenomena are found. When $0.9943 \le \alpha_1 \le 1$,the fractional-order Lorenz-like system is chaotic and the dynamics of this system becomes regular if $\alpha_3<0.9943$. Therefore,the results imply that the minimum effective dimension $\Sigma_{cr}=2.8485$. The dynamical portrait of this system is shown in Fig. 3.

|
Download:
|
| Fig. 3. Chaotic attractor of fractional-order Lorenz-like system (8) with parameters $(a,b,c,\alpha_1,\alpha_2,\alpha_3)=(10,100,11.2,0.8485,1,1)$ and the effective dimension $\Sigma=2.8485$. | |
In this case,the maximal Lyapunov exponent can be estimated as $\lambda_{\rm max}\approx 0.3833$. In particular,the obtained critical values of the parameters $\alpha_1,~\alpha_2,~\alpha_3$ reflect the fact that the linear differential equation (first equation) in fractional-order Lorenz-like system seems to be less "sensitive" to the damping,introduced by a fractional derivative, than two other nonlinear equations. As can be seen from the maximal Lyapunov exponents spectrum with respect to the varying parameter $\alpha$ in (8),shown in Fig. 4 (a),it has been found that when $\alpha \in [0.9950,1]$,the fractional order system exhibits chaos. Similarly,the maximal Lyapunov exponents spectrum with respect to the varying parameter $\alpha_i$ in (23),is shown in Fig. 4 (b)-(d),respectively.

|
Download:
|
| Fig. 4. Maximal Lyapunov exponents spectrum of fractional-order Lorenz-like system (8) with parameters $(a,b,c)=(10, 100, 11.2)$ on (a) $\alpha=\alpha_1=\alpha_2=\alpha_3 \in (0.9949,1)$, (b) $\alpha_2=\alpha_3=1,\alpha_1 \in (0.8485,1)$, (c) $\alpha_1=\alpha_3=1,\alpha_2 \in (0.9990,1)$, (d) $\alpha_1=\alpha_2=1,\alpha_3 \in (0.9943,1)$, respectively. | |
Synchronization of fractional-order chaotic systems has driven a great interest and is studied keenly due to its vast applications in various fields such as secure communications,signal and control processing and encryption[29, 30, 31, 32, 33, 34, 35] and as result a variety of synchronization methods are developed and studied such as generalized projective synchronization[32],network synchronization[33]. Some authors of the above mentioned literature about synchronization of fractional order systems are concerned with common drive-response type of synchronization with one drive and one response system as well as multi-chaotic synchronization methods such as combination synchronization using active backstepping design[36, 37]. Therefore,we are motivated to study the combination synchronization with the help of nonlinear feedback control method of the fractional order system (8) for commensurate order. The corresponding drive-response systems of system (8) are expressed,respectively,as
| $ \left\{ \begin{array}{l} D_t^\alpha x_m = a(y_m - x_m ),\\ D_t^\alpha y_m = -c y_m - x_m z_m ,\\ D_t^\alpha z_m = - b + x_m y_m. \\ \end{array} \right. \label{drivecommen} $ | (24) |
where $m=1,2$ and
| $ \left\{ \begin{array}{l} D_t^\alpha x_s = a(y_s - x_s ) + u_1,\\ D_t^\alpha y_s = -c y_s - x_s z_s + u_2,\\ D_t^\alpha z_s = - b + x_s y_s + u_3.\\ \end{array} \right. \label{responsecommen} $ | (25) |
where $(a,b,c,\alpha)=(10,100,11.2,0.996)$ and $u_i$ $(i=1,2,3)$ are controllers such that the three systems can be synchronized.
Define the error variables by $e=Ax+By-Cz$,where $x=(x_1,y_1, z_1)^{\rm T},y=(x_2,y_2,z_2)^{\rm T}$,$z=(x_s,y_s,z_s)^{\rm T}$,$e=(e_1,e_2,e_3)$,$A,B,C \in {\bf R}^{3\times 3}$. Choose some suitable control functions $u_i (i=1,2,3)$,such that $\lim\nolimits_{t\rightarrow \infty}\|Ax+By-Cz\|=0$,then the three systems will approach synchronization. For the convenience of our discussions,we assume that $A={\rm diag}(\eta_1,\eta_2,\eta_3)$, $B={\rm diag}(\gamma_1,\gamma_2,\gamma_3)$,$C={\rm diag}(1,1, 1)$,We get the relevant error system as follows:
| $ \left\{ \begin{array}{l} D_t^\alpha e_1 = \eta_1 D_t^\alpha x_1+\gamma_1 D_t^\alpha x_2- D_t^\alpha x_s,\\ D_t^\alpha e_2 = \eta_2 D_t^\alpha y_1+\gamma_2 D_t^\alpha y_2- D_t^\alpha y_s,\\ D_t^\alpha e_3 = \eta_3 D_t^\alpha z_1+\gamma_3 D_t^\alpha z_2- D_t^\alpha z_s,\\ \end{array} \right. $ | (26) |
i.e.,
| $ \left\{ \begin{array}{l} D_t^\alpha e_1 =-a e_1+a e_2 +a(\eta_1-\eta_2)y_1 \\ \ \ \ \ \ \ \ \ \ \ +a(\gamma_1-\gamma_2)y_2-u_1,\\ D_t^\alpha e_2 =-ce_2-\eta_2x_1z_1-\gamma_2 x_2 z_2+x_s z_s-u_2,\\ D_t^\alpha e_3 =b(-\eta_3-\gamma_3+1)+\eta_3x_1y_1+\gamma_3x_2y_2 \\ \ \ \ \ \ \ \ \ \ \ -x_sy_s-u_3. \end{array} \right.\label{erro2} $ | (27) |
Theorem 2. With the control functions
| $\left\{ \begin{array}{l} u_1 = a(\eta_1-\eta_2)y_1+a(\gamma_1-\gamma_2)y_2-v_1,\\ u_2 =-\eta_2x_1z_1-\gamma_2 x_2 z_2+x_s z_s-v_2,\\ u_3 =b(-\eta_3-\gamma_3+1)+\eta_3x_1y_1+\gamma_3x_2y_2-x_sy_s-v_3,\\ \end{array} \right. \label{controlterm1} $ | (28) |
and the terms $v_i$ are chosen by suitable linear functions of the errors terms $e_i$ ($i=1,2,3$),the driven systems (24) will achieve combination synchronization with the response system (25).
Proof. With the control functions $(28)$,the error system $(27)$ becomes
| $ \left\{ \begin{array}{l} D_t^\alpha e_1 =-a e_1+a e_2 +v_1,\\ D_t^\alpha e_2 =-ce_2+v_2,\\ D_t^\alpha e_3 =v_3.\\ \end{array} \right.\label{erro2form} $ | (29) |
We choose
| $ \left( {\begin{array}{*{20}{c}} v_1 \\ v_2 \\ v_3 \\ \end{array}} \right)=\overline{A}\left( {\begin{array}{*{20}{c}} e_1 \\ e_2 \\ e_3 \\ \end{array}} \right), $ | (30) |
where
| $ \overline{A}=\left( {\begin{array}{*{20}{c}} a_{11}& a_{12} & a_{13} \\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \\ \end{array}} \right) $ | (31) |
is a $3\times 3$ real matrix. Based on the $v_i$,we need to make the conditions of Lemma 1 satisfied,i.e.,$|\arg(\lambda)|> \alpha \pi/2$. If we choose $a_{11}=0$,$a_{12}=0$,$a_{13}=0$, $a_{21}=0$,$a_{22}=0$,$a_{23}=0$,$a_{31}=0 $,$a_{32}=0$, $a_{33}=-1$,then the error system is
| $ \left\{ \begin{array}{l} D_t^\alpha e_1 =-a e_1+a e_2,\\ D_t^\alpha e_2 =-ce_2,\\ D_t^\alpha e_3 =-e_3.\\ \end{array} \right.\label{errodetail} $ | (32) |
Since $(a,b,c,\alpha)=(10,100,11.2,0.996)$,we get $\lambda_1=-10$,$\lambda_2=-11.2$,$\lambda_3=-1$,i.e., $|\arg(\lambda)|> \alpha \pi/2$ is satisfied.
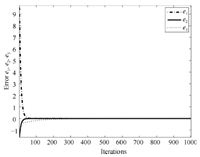
1) Numerical simulation: Based on the Theorem 2,we choose $(a,b,c,\alpha)=(10,100,11.2, 0.996)$ with initial values $(e_1(0),e_2(0),e_3(0))=(10.98,-1.82, -0.49)$,control functions (28) and $\overline{A}$,then the error system (32) converges to zero with any initial values as Fig. 5 shows.
|
Download:
|
| Fig. 5. Synchronization of the drive system (24) and response system (25) with commensurate order $\alpha=0.996$,$e_i(t)\rightarrow 0$ as $t\rightarrow \infty$ $i=1,2,3$. | |
2) Some remarks: a) In this case,the choice of the $A={\rm diag}(\eta_1,\eta_2, \eta_3)$,$B={\rm diag}(\gamma_1,\gamma_2,\gamma_3)$ has no effect on the stability of the error system. b) When $A=I,B=0$ or $A=0, B=I$,then the combination synchronization degenerates into two systems of synchronization in the traditional sense.
B. Synchronization Analysis of Incommensurate CaseWe consider the following drive system:
| $ \left\{ \begin{array}{l} D_t^{\alpha_1} x_m = a(y_m - x_m ),\\ D_t^{\alpha_2} y_m = -c y_m - x_m z_m ,\\ D_t^{\alpha_3} z_m = - b + x_m y_m. \\ \end{array} \right. $ | (33) |
where $m=1,2$ and response system
| $ \left\{ \begin{array}{l} D_t^{\alpha_1} x_s = a(y_s - x_s ) + u_1,\\ D_t^{\alpha_2} y_s = -c y_s - x_s z_s + u_2,\\ D_t^{\alpha_3} z_s = - b + x_s y_s + u_3.\\ \end{array} \right. $ | (34) |
where $(a,b,c)=(10,100,11.2)$,$(\alpha_1,\alpha_2, \alpha_3)=(0.96,1,1)$ and $u_i$ $(i=1,2,3)$ are controllers such that the three systems can be synchronized.
Theorem 3. Under suitable choice of the active control functions $u_i$ $(i=1,2,3)$,then the drive system (33) will achieve combination synchronization with the response system (34).
Proof. Similar to the analysis of the Theorem 2,with the control functions (28),we get error system
| $ \left\{ \begin{array}{ll} D_t^{\alpha_1} e_1 =-a e_1+a e_2 +v_1,\\ D_t^{\alpha_2} e_2 =-ce_2+v_2,\\ D_t^{\alpha_3} e_3 =v_3,\\ \end{array} \right. $ | (35) |
where $v_i (i=1,2,3)$ is represented in (1). If we choose $a_{11}=0$,$a_{12}=0$,$a_{13}=0$,$a_{21}=0$,$a_{22}=0$, $a_{23}=0$,$a_{31}=0 $,$a_{32}=0$,$a_{33}=-1$,then the error system is
| $ \left\{ \begin{array}{l} D_t^{\alpha_1}e_1 =-a e_1+a e_2,\\ D_t^{\alpha_2}e_2 =-ce_2,\\ D_t^{\alpha_3}e_3 =-e_3.\\ \end{array} \right. $ | (36) |
Based on the Lemma 4,here,$m=100,\gamma=1/100$,then the equation ${\rm det}({\rm diag}(\lambda^{m\alpha_1},\lambda^{m\alpha_2},\lambda^{m\alpha_3})-A)=0$ can be written as $(\lambda^{96}+a)(\lambda^{100}+c)(\lambda^{100}+1)=0$,where
| $ A=\left( {\begin{array}{*{20}{c}} -a& a & 0 \\ 0& -c &0 \\ 0& 0& -1 \\ \end{array}} \right). $ | (37) |
Since $a=10,c=11.2$,i.e., $(\lambda^{96}+10)(\lambda^{100}+11.2)(\lambda^{100}+1)=0$,its roots satisfy at least one equation of $\lambda^{96}+10=0$, $\lambda^{100}+11.2=0$ and $\lambda^{100}+1=0$. Assume that $\lambda^{96}+10=0$,then we suppose its roots are $\lambda=r(\cos\theta+i\sin\theta)$,i.e., $r^{96}(\cos96\theta+i\sin96\theta)=10(\cos\pi+i\sin\pi)$ $\Rightarrow \min\theta=\pi/96$. All other cases are similar. These all roots lie in the region $|{\rm arg}(\lambda)|>\pi/200$. Thus, the drive system (33) and the response system (34) achieve combination synchronization.
1) Numerical simulation: Based on the Theorem 3,we choose $(a,b,c,\alpha_1,\alpha_2, \alpha_3)=(10,100,11.2,0.996,1,1)$,and randomly choose initial values $(e_1(0),e_2(0),e_3(0))=(2.1,-3.82,3.49)$,control functions (28) and $\overline{A}$,then the error system (36) converges to zero with any initial values as shown in Fig. 6.

|
Download:
|
| Fig. 6. Synchronization of the drive systems (33) and response system (34) with commensurate order $(\alpha_1, \alpha_2,\alpha_3)=(0.96,1,1)$,$e_i(t)\rightarrow 0$ as $t\rightarrow \infty$, $i=1,2,3$. | |
2) Some remarks: a) In this case,the choice of $A={\rm diag}(\eta_1,\eta_2, \eta_3)$,$B={\rm diag}(\gamma_1,\gamma_2,\gamma_3)$ has no effect on the stability of the error system. But,$e=Ax+By-Cz$,so the orbits of error $e$ are constructed of linear combination of $x(t), y(t),z(t)$. Essentially,$e(t)$ is influenced by $x(t),y(t), z(t)$. b) Control functions are more complex. How to simplify the control function is a common problem in chaos synchronization. c) Initial values of error system are chosen randomly. It has no influence on the convergence of the error system. d) In Theorems 2 and 3,a suitable choice of the control function is a function which makes the original nonlinear system a linear error system,moreover the obtained linear error system is stable at origin $(0,0,0)$.
Ⅴ. CONCLUSIONSThis paper has proposed a new fractional-order Lorenz-like system. As a matter of fact,the eigenvalues structure associated to the equilibria of the new fractional-order Lorenz-like system makes it topologically not equivalent to the original fractional-order Lorenz and Chen systems,the new system has only two stable node-foci while all the other similar typical fractional-order chaotic systems have a saddle and two unstable saddle-foci or a saddle and two stable node-foci. In this paper,some sufficient conditions for local stability of equilibria are given based on stability theorems of fractional-order systems. Further study of the chaotic dynamics of the system is observed numerically. The results reveal that fractional-order Lorenz-like system can display chaotic attractor with effective dimension less than three. The dynamics of the system is vigorously sensitive to the values of effective dimension $\Sigma$. In general,decreasing of the parameters $\alpha$ leads to a damping in the system. The minimum effective dimension $\Sigma_{cr}$ for fractional-order Lorenz-like system is estimated as 2.8485,below which the dynamics of the system falls into a regular region. In particular, the results signify the fact that the linear differential equation (first equation) in fractional-order Lorenz-like system seems to be less "sensitive" to the damping,introduced by a fractional derivative,than two other nonlinear equations. Furthermore,the combination synchronization in fractional-order Lorenz-like system is analyzed,where three systems are synchronized,the first two of them are drive type,while the third is response system. For combination synchronization,some sufficient conditions were satisfied. In order to show the effectiveness of the design, numerical simulations are given. Combination synchronization, being an extension of the typical synchronization has the capability of applications widely in Electrical Engineering, secure communication etc. In a common drive-response scheme,the drive system is responsible for transmission of the signal, however for the combination synchronization discussed in this paper,two different chaotic systems are capable of transmitting signal which might have harder anti-hack capability than transmitted by a typical drive-response model.
| [1] | Oldham K B, Spanier J. The Fractional Calculus. New York: Academic Press, 1974. |
| [2] | Hilfer R. Applications of Fractional Calculus in Physics. New Jersey: World Scientific, 2000. |
| [3] | Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations. San Diego: Elsevier, 2006. |
| [4] | Hirsch M W, Smale S. Differential Equations, Dynamical Systems and Linear Algebra. New York: Academic Press, 1974. |
| [5] | Hartley T T, Lorenzo C F, Qammer H K. Chaos in a fractional order Chua's system. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 1995, 42(8): 485-490 |
| [6] | Grigorenko I, Grigorenko E. Chaotic dynamics of the fractional Lorenz system. Physical Review Letters, 2003, 91(3): 034101 |
| [7] | Li C P, Chen G R. Chaos in the fractional order Chen system and its control. Chaos, Solitons & Fractals, 2004, 22(3): 549-554 |
| [8] | Petravs I. Chaos in the fractional-order Volta's system: modeling and simulation. Nonlinear Dynamics, 2009, 57: 157-170 |
| [9] | Yang Q G, Zeng C B. Chaos in fractional conjugate Lorenz system and its scaling attractors. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(12): 4041-4051 |
| [10] | Li C G, Chen G R. Chaos and hyperchaos in the fractional order Rossler equations. Physica A: Statistical Mechanics and Its Applications, 2004, 341: 55-61 |
| [11] | Maouk A E. Stability conditions, hyperchaos and control in a novel fractional order hyperchaotic system. Physics Letters A, 2009, 373(25): 2166-2173 |
| [12] | Zeng C B, Yang Q G, Wang J W. Chaos and mixed synchronization of a new fractional-order system with one saddle and two stable node-foci. Nonlinear Dynamics, 2011, 65(4): 457-466 |
| [13] | Podlubny I. Fractional Differential Equations. San Diego: Academic Press, 1998. |
| [14] | Yang Q G, Wei Z C, Chen G R. An unusual 3D autonomous quadratic chaotic system with two stable node-foci. International Journal of Bifurcation and Chaos, 2010, 20(4): 1061-1083 |
| [15] | Matignon D. Stability results for fractional differential equations with applications to control processing. In: Proceedings of the 1996 International Conference on Computational Engineering in Systems and Application. Lille, France, 1996. 963-968 |
| [16] | Diethelm K, Ford N J. Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications, 2002, 265(2): 229-248 |
| [17] | Li C P, Ma Y T. Fractional dynamical system and its linearization theorem. Nonlinear Dynamics, 2013, 71(4): 621-633 |
| [18] | Deng W H, Li C P, Lu J H. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dynamics, 2007, 48(4): 409-416 |
| [19] | Barnett S. Polynomials and Linear Control Systems. New York: Marcel Dekker, 1983. |
| [20] | Diethelm K, Ford N J, Freed A D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dynamics, 2002, 29(1-4): 3-22 |
| [21] | Cafagna D, Garssi G. Fractional-order chua's circuit: time-domain analysis, bifurcation, chaotic behavior and test for chaos. International Journal of Bifurcation and Chaos, 2008, 18(3): 615-639 |
| [22] | Cafagna D, Grassi G. Bifurcation and chaos in the fractional-order chen system via a time-domain approach. International Journal of Bifurcation and Chaos, 2008, 18(7): 1845-1863 |
| [23] | Alomari A K, Noorani M S M, Nazar R, Li C P. Homotopy analysis method for solving fractional Lorenz system. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(7): 1864-1872 |
| [24] | Tavazoei M S, Haeri M. Limitations of frequency domain approximation for detecting chaos in fractional order systems. Nonlinear Analysis: Theory, Methods & Applications, 2008, 69(4): 1299-1320 |
| [25] | Deng W H, Li C P. The evolution of chaotic dynamics for fractional unified system. Physics Letters A, 2008, 372(4): 401-407 |
| [26] | Wolf A, Swift J B, Swinney H L, Vastano J A. Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena, 1985, 16: 285-317 |
| [27] | Eckmann J P, Kamphorst S O, Ruelle D, Ciliberto S. Liapunov exponents from time series. Physical Review A, 1986, 34(6): 4971-4979 |
| [28] | Rosenstein M T, Collins J J, De Luca C J. A practical method for calculating largest lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena, 1993, 65(1-2): 117-134 |
| [29] | Muthukumar P, Balasubramaniam P. Feedback synchronization of the fractional order reverse butterfly-shaped chaotic system and its application to digital cryptography. Nonlinear Dynamics, 2013, 74(4): 1169-1181 |
| [30] | Zhou T S, Li C P. Synchronization in fractional-order differential systems. Physica D: Nonlinear Phenomena, 2005, 212(1-2): 111-125 |
| [31] | Lu J G. Chaotic dynamics of the fractional order Lu system and its synchronization. Physics Letters A, 2006, 354(4): 305-311 |
| [32] | Wu X J, Lu Y. Generalized projective synchronization of the fractionalorder Chen hyperchaotic system. Nonlinear Dynamics, 2009, 57(1-2): 25-35 |
| [33] | Wang J W, Zhang Y B. Network synchronization in a population of star-coupled fractional nonlinear oscillators. Physics Letters A, 2010, 374(13-14): 1464-1468 |
| [34] | Odibat Z M. Adaptive feedback control and synchronization of nonidentical chaotic fractional order systems. Nonlinear Dynamics, 2010, 60(4): 479-487 |
| [35] | Yuan L G, Yang Q G. Parameter identification and synchronization of fractional-order chaotic systems. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(1): 305-316 |
| [36] | Luo R Z, Wang Y L, Deng S C. Combination synchronization of three classic chaotic systems using active backstepping design. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2011, 21(4): 043114 |
| [37] | Luo R Z, Wang Y L. Finite-time stochastic combination synchronization of three different chaotic systems and its application in secure communication. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2012, 22(2): 023109 Scientific, 2000. |
 2016, Vol.3
2016, Vol.3 


