2. College of Transportation, Shandong University of Science and Technology, Qingdao 266590, China
The linear estimation problem has been an important
control and signal processing community research topic since Wiener
filtering
The singular system optimal filter corrupted by multiplicative
noises has also been studied well in recent years[10, 11, 12, 13].
Particularly,in
It should be noted that,the above references have not considered
the singular multiplicative noise systems with delayed
measurement,for which state augmentation approach is usually
applied for non-singular systems[2, 3],however,the state
augmentation approach used to require large calculation amount.
The optimal multi-step predictor for singular systems corrupted by
multiplicative noises and with delay-observations has been given
in
The paper focuses on the linear discrete-time singular system corrupted by multiplicative noise,delayed measurements and known coefficients matrices as
| $ F{ x}(t+1) = A { x}(t)+B{ u}(t),~\label{e2.1} $ | (1) |
| $ { y}(t)=C{ x}(t)+D{ w}(t){ x}(t)+{ v}(t),~\label{e2.2} $ | (2) |
| $ { y}_d(t)=C_d{ x}(t(d))+D_{d}{ w}(t){ x}(t(d))+{ v}_d(t),~\label{e2.3} $ | (3) |
where $t(d)=t-d$,the variables ${ x}(t)\in {\bf R}^{n}$,${ y}(t)\in R^{q}$,${ y}_d(t)$ $\in$ ${\bf R}^{q_d}$,${ u}(t)\in R^{p}$,${ v}(t)\in {\bf R}^{q}$,${ v}_d(t)\in R^{q_d}$,and${ w}(t)\in R^1$ is respectively the state,instantaneous measurement, delayed measurement,and noises (including input,observation noises,and multiplicative noise),and the other noises are also uncorrelated with known variance matrices as in [14, 15, 16, 18, 19].
Before giving the problem to be dealt with,two assumptions will first be given similar to [14, 15, 19] as follows:
Assumption 1. $F$ is singular,and the system plant (1)-(3) is regular.
Assumption 2. The system is impulse free system.
The main problem in this paper can be described as follows:
Given the sequence of measurements ${ y}(s)|_{s=0}^t$ and the sequence of delayed measurements ${ y}_d(s)|_{s=d}^t$,find Kalman filter $\hat { x}(t|t)$ of ${ x}(t)$,where ${\bf \xi}(s)|_{s=0}^t=\xi(0),\xi(1),...,\xi(t)$.
III.MAIN RESULTS A.Restricted Equivalent Delayed SystemUnder Assumptions 1 and 2,in accordance with the traditional singular system result in [12, 13, 14, 16],there exist nonsingular matrices $\{J_1,J_2\}\in R^{n\times n}$,${ x}(t)=J_2[{{ x}_1(t)} { x}_2(t)]$,and the restricted equivalent system can be given as follows
| $ { x}_1(t+1) =\ A_1 { x}_1(t)+B_1{ u}(t), $ | (4) |
| $ { y}(t)=\ C_1{ x}_1(t)+C_2{ x}_2(t)+D_1{ w}(t){ x}_1(t) $ | (5) |
| $ \begin{array}{l} {F_1}{x_2}(t + 1) = \;{x_2}(t) + {B_2}u(t),\; + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{D_2}w(t){x_2}(t) + v(t), \end{array} $ | (6) |
| $ \begin{array}{l} {y_d}(t) = \;{C_{1d}}{x_1}(t(d)) + {C_{2d}}{x_2}(t(d))\; + \\ \;\;\;\;\;\;\;\;\;{D_{1d}}w(t){x_1}(t(d))\; + \\ \;\;\;\;\;\;\;\;{D_{2d}}w(t){x_2}(t(d)) + {v_d}(t), \end{array} $ | (7) |
where $F_1,A_1,B_1,B_2,C_1,...,D_{2d}$ can be referred to
Remark 1. The restricted delayed system (4)-(7) is presented
by using standard singular value decomposition,and it is equivalent
to the singular system (1)-(3),so we can first give the Kalman
filters for ${ x}_1(t)$ and ${ x}_2(t)$ in (4)-(7),then the
needed Kalman filter $\hat{ x}(t|t)$ can be indirectly yielded
from $\hat{ x}_1(t|t)$ and $\hat{ x}_2(t|t)$. For the
restricted delayed system,Kalman filtering cannot be used directly
due to the existence of delayed measurement and multiplicative
noise. Usually,such a problem can be solved by system
augmentation
First,we denote $Y_o(t)$ as the measurements of the system model (4)-(7),thus for $t\geq d$,we have
| $ Y_o(t)=\left[\begin{array}{*{20}c}{ y}(t) \\ { y}_d(t)\end{array}\right]. $ | (8) |
This paper will pay attention to the case of $t\geq d$,when $t$ $<$ $d$,(7) cannot be used,$Y_o(t)$ is just ${ y}(t)$,and the problem will be the Kalman filtering for singular systems without delay which has been dealt with before.
Define
| $ {Y_2}(t) = \left[{\begin{array}{*{20}{c}} {y(t)}\\ {{y_d}(t + d)} \end{array}} \right], $ | (9) |
| $ {Y_1}(t) = y(t), $ | (10) |
then,similar to
(6) and (7) can be rewritten as
| $ \begin{array}{l} {Y_i}(t) = \;{C_{1i}}{x_1}(t) + {C_{2i}}{x_2}(t) + {D_{1i}}(w,t){x_1}(t)\\ \;\;\;\;\;\;\;\;\;\; + {D_{2i}}(w,t){x_2}(t) + {V_i}(t),\quad i = 1,2, \end{array} $ | (11) |
where ${\cal C}_{11},{\cal C}_{12},...,{\cal D}_{22}(w,t)$ can be
given as in
| $ { x}_1(t)=A^t_1{ x}_1(0)+\sum_{i=0}^{t-1}A_1^{t-i-1}B_1{ u}(i),\label{e3.16} $ | (12) |
| $ { x}_2(t)=-\sum_{i=0}^{\lambda-1}F_1^iB_2{ u}(t+i). $ | (13) |
Take (12) and (13) into (11),we have
| $ {\cal Y}_i(t)={\cal C}_{1i} { x}_1(t)+{\cal D}_{1i}(w,t) { x}_1(t)+{\bar {\cal V}}_i(t),~~~\label{e3.18} $ | (14) |
where
| $ {\bar {\cal V}}_i(t)=\ {\cal V}_i(t)-{\cal C}_{2i} \sum_{j=0}^{\lambda-1}F_1^jB_2{ u}(t+j) -{\cal D}_{2i}(w,t) \sum_{j=0}^{\lambda-1}F_1^jB_2{ u}(t+j),\quad i=1,2. $ |
The
re-organization of innovation lemma for the restricted equivalent
delayed system (4)-(7) will be presented in this part,some
definitions of $\hat{\xi}(t|s)$ and $\hat{\eta}(\tau,i)$ $(i=$
$1,2)$ can be referred to
Lemma 1. ${\cal L}\{\tilde{\cal Y}_2(s)|_{s=0}^{t(d)};\tilde{\cal Y}_1(s)|_{s=t(d)+1}^t\}$ is an innovation sequence,and the spanned linear space is equivalent to ${\cal L}\{{\cal Y}_2(s)|_{s=0}^{t(d)};{\cal Y}_1(s)|_{s=t(d)+1}^t\}.$
Proof. The lemma can be given similar to
Consider (14) with the projection theorem,we have
| $ \hat{\cal Y}_i(t,i)={\cal C}_{1i}\hat{ x}_1(t,i)+\hat{\bar{\cal V}}_i(t,i), $ | (15) |
thus,combining (14) with (15) yields
| $ \tilde{{\cal Y}}_i(t)={\cal C}_{1i}{ e}_1(t,i)+{\cal D}_{1i}(w,t){ x}_1(t)+\tilde{{\bar{\cal V}}}_i(t).\label{e3.30} $ | (16) |
In this part,the error covariance matrix $P_1(t(d)+k+1,i)$ of ${ e}_1(t(d)+k+1,i)$ will be given.
By using traditional Kalman filtering with multiplicative noises [11, 13, 14, 16, 17],we can similarly give the recursive equation of $P_1(t(d)+1,2)=\langle{ e}_1(t(d)+1,2),{ e}_1(t(d)+1,2)\rangle$ with the initial values $G(0,0,2)=T(0,0,2),$ $G_1(0,0,2)=$ $G_3(0,$ $0|-1,2)=H_1(0,0,2)=H_2(0,0|-1,2)=0$,so the main problem is to present the recursive equation of $P_1(t(d)$ $+$ $k+1,1)$.
$P_1(t(d)+k+1,1)$ for $k=1,...,d-1$ can be further given as in
Theorem 1 of
From (16),since ${ x}_1(t(d)+k)=\hat{ x}_1(t(d)+k,1)+{ e}_1(t(d)$ $+$ $k,1)$,$\hat{ x}_1(t(d)+k,1)\perp \tilde{{\cal Y}}_1(t(d)+k)$,${\tilde{\bar{\cal V}}}_1(t(d)+k)=\bar{\cal V}_1(t(d)$ $+$ $k)-{\hat{\bar{\cal V}}}_1(t(d)+k,1)$ and ${ e}_1(t(d)+k,1)\perp {\hat{\bar{\cal V}}}_1(t(d)+k)$,then we have
| $ \begin{array}{l} L(t(d) + k,t(d) + k,1)\\ = \langle {x_1}(t(d) + k),{\widetilde Y_1}(t(d) + k)\rangle \quad \\ = \langle {e_1}(t(d) + k,1),{\widetilde Y_1}(t(d) + k)\rangle \quad \\ = {P_1}(t(d) + k,1)C_{11}^{\rm{T}} + \langle {e_1}(t(d) + k,1),{\widetilde {\overline V }_1}(t(d) + k)\rangle \quad \\ = {P_1}(t(d) + k,1)C_{11}^{\rm{T}} + \langle {e_1}(t(d) + k,1),{\overline V _1}(t(d) + k)\quad \quad \\ - {\widehat {\overline V }_1}(t(d) + k,1)\rangle \\ = {P_1}(t(d) + k,1)C_{11}^{\rm{T}} + H_1^{\rm{T}}(t(d) + k,t(d) + k,1). \end{array} $ | (17) |
From (16),we have
| $ Q_{\tilde{\cal Y}_1}(t(d)+k) \\ \quad =\langle\tilde{\cal Y}_1(t(d)+k),\tilde{\cal Y}_1(t(d)+k)\rangle \\ \quad ={\cal C}_{11}P_1(t(d)+k,1){\cal C}_{11}^{\rm T} \\ \quad\quad +{\cal C}_{11}\langle{ e}_1(t(d)+k,1),\bar{\cal V}_1(t(d)+k)\rangle \\ \quad\quad -{\cal C}_{11}\langle{ e}_1(t(d)+k,1),{\hat{\bar{\cal V}}}_1(t(d)+k,1)\rangle \\ \quad\quad +D_1M\Pi_1(t(d)+k)D_1^{\rm T} \\ \quad\quad +\langle{\bar{\cal V}}_1(t(d)+k),{ e}_1(t(d)+k,1)\rangle{\cal C}_{11}^{\rm T} \\ \quad\quad +R(t(d)+k,t(d)+k,1) \\ \quad\quad -\langle{\hat{\bar{\cal V}}}_1(t(d)+k,1),{ e}_1(t(d)+k,1)\rangle{\cal C}_{11}^{\rm T} \\ \quad\quad -\langle{\bar{\cal V}}_1(t(d)+k),{\hat{\bar{\cal V}}}_1(t(d)+k,1)\rangle \\ \quad\quad -\langle{\hat{\bar{\cal V}}}_1(t(d)+k,1),{\bar{\cal V}}_1(t(d)+k)\rangle \\ \quad\quad +\langle{\hat{\bar{\cal V}}}_1(t(d)+k,1),{\hat{\bar{\cal V}}}_1(t(d)+k,1)\rangle \\ \quad ={\cal C}_{11}P_1(t(d)+k,1){\cal C}_{11}^{\rm T}+D_1M\Pi_1(t(d)+k)D_1^{\rm T} \\ \quad\quad +R(t(d)+k,t(d)+k,1) \\ \quad\quad -H_2(t(d)+k,t(d)+k|t(d)+k-1,1) \\ \quad\quad +{\cal C}_{11}H_1^{\rm T}(t(d)+k,t(d)+k,1) \\ \quad\quad +H_1(t(d)+k,t(d)+k,1){\cal C}_{11}^{\rm T}. \label{e3.56} $ | (18) |
Combining (4) with $\Pi_1(t(d)+k+1)=\langle{ x}_1(t(d)+k+1),$ ${ x}_1(t(d)+k+1)\rangle$ yields
| $ \Pi_1(t(d)+k+1)=A_1\Pi_1(t(d)+k)A_1^{\rm T} +B_1Q_uB_1^{\rm T},\label{e3.57a} $ | (19) |
and from
| $ \begin{array}{l} R(t(d) + k,t(d) + k,1)\\ = {Q_v} + \sum\limits_{j = 0}^{\lambda - 1} {{C_{21}}} F_1^j{B_2}{Q_u}B_2^{\rm{T}}{(F_1^j)^{\rm{T}}}C_{21}^{\rm{T}} + \\ M\sum\limits_{j = 0}^{\lambda - 1} {{D_2}} F_1^j{B_2}{Q_u}B_2^{\rm{T}}{(F_1^j)^{\rm{T}}}D_2^{\rm{T}}. \end{array} $ | (20) |
From the well-known projection theorem,
| $ \hat{ x}_1(t(d)+k+1,1) \\[1mm] \quad ={\rm Proj}\{{ x}_1(t(d)+k+1)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)}; \tilde{\cal Y}_1(s)|_{s=t(d)+1}^{t(d)+k}\} \\[1mm] \quad ={\rm Proj}\{A_1{ x}_1(t(d)+k) \\[1mm] \quad\quad +B_1{ u}(t(d)+k)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)}; \tilde{\cal Y}_1(s)|_{s=t(d)+1}^{t(d)+k-1}\} \\[1mm] \quad\quad +{\rm Proj}\{A_1{ x}_1(t(d)+k)+B_1{ u}(t(d)+k) \\[1mm] \quad\quad \times |\tilde{\cal Y}_1(t(d)+k)\} \\[1mm] \quad =A_1\hat{ x}_1(t(d)+k,1)+B_1\hat{ u}(t(d)+k,1) \\[1mm] \quad\quad +A_1{\rm Proj}\{{ x}_1(t(d)+k)|\tilde{\cal Y}_1(t(d)+k)\} \\[1mm] \quad\quad +B_1{\rm Proj}\{{ u}(t(d)+k)|\tilde{\cal Y}_1(t(d)+k)\} \\[1mm] \quad =A_1\hat{ x}_1(t(d)+k,1) \\[1mm] \quad\quad +A_1K(t(d)+k,1)\tilde{\cal Y}_1(t(d)+k) \\[1mm] \quad\quad +B_1\hat{ u}(t(d)+k|t(d)+k,1),\label{e3.59} $ | (21) |
where
| $ K(t(d)+k,1)=L(t(d)+k,t(d)+k,1) Q_{\tilde{\cal Y}_1}^{-}(t(d)+k),\label{e3.54} $ | (22) |
then by considering (4) and (21),we have
| $ { e}_1(t(d)+k+1,1) \\[1mm] \quad =A_1{ e}_1(t(d)+k,1)+B_1{ u}(t(d)+k) \\[1mm] \quad\quad -B_1\hat{ u}(t(d)+k|t(d)+k,1)\\[1mm] \quad\quad -A_1K(t(d)+k,1)\tilde{\cal Y}_1(t(d)+k).\label{e3.60} $ | (23) |
Since ${ e}_1(t(d)+k+1,1)$ is uncorrelated with $\tilde{\cal Y}_1(t(d)+k)$,so from (23) it can be easily yielded as
| $ P_1(t(d)+k+1,1)+A_1K(t(d)+k,1) \\[1mm] \quad\quad \times Q_{\tilde{\cal Y}_1}(t(d)+k)K^{\rm T}(t(d)+k,1)A_1^{\rm T}\\[1mm] \quad =A_1P_1(t(d)+k,1)A_1^{\rm T} \\[1mm] \quad\quad +A_1\langle{ e}_1(t(d)+k,1),{ u}(t(d)+k)\rangle B_1^{\rm T} \\[1mm] \quad\quad -A_1\langle{ e}_1(t(d)+k,1),\hat{ u}(t(d)+k|t(d)+k,1)\rangle \\[1mm] \quad\quad \times B_1^{\rm T}+B_1Q_uB_1^{\rm T} \\[1mm] \quad\quad + B_1\langle{ u}(t(d)+k),{ e}_1(t(d)+k,1)\rangle A_1^{\rm T} \\[1mm] \quad\quad -B_1\langle{ u}(t(d)+k),\hat{ u}(t(d)+k|t(d)+k,1)\rangle B_1^{\rm T} \\[1mm] \quad\quad +B_1\langle\hat{ u}(t(d)+k|t(d)+k,1),\\[1mm] \quad\quad\ \hat{ u}(t(d)+k|t(d)+k,1)\rangle B_1^{\rm T} \\[1mm] \quad\quad -B_1\langle\hat{ u}(t(d)+k|t(d)+k,1),{ e}_1(t(d)+k,1)\rangle A_1^{\rm T} \\[1mm] \quad\quad -B_1\langle\hat{ u}(t(d)+k|t(d)+k,1),{ u}(t(d)+k)\rangle B_1^{\rm T} \\[1mm] \quad =A_1P_1(t(d)+k,1)A_1^{\rm T}+B_1[Q_u \\[1mm] \quad\quad -G_3(t(d)+k,t(d)+k|t(d)+k,1)]B_1^{\rm T} +A_1G_1^{\rm T}(t(d)+k,t(d)+k,1)B_1^{\rm T} \\[1mm] +B_1G_1(t(d)+k,t(d)+k,1)A_1^{\rm T} .\label{e3.61} $ | (24) |
According to the projection theorem,we have
| $ \hat{{ u}}(t(d)+k|s,1) \\ \quad ={\rm Proj}\{{ u}(t(d)+k)|\tilde{\cal Y}_2(s_1)|_{s_1=0}^{t(d)};\tilde{\cal Y}_1(s_1)|_{s_1=t(d)+1}^{s}\} \\ \quad ={\rm Proj}\{{ u}(t(d)+k)|\tilde{\cal Y}_2(s_1)|_{s_1=0}^{t(d)};\tilde{\cal Y}_1(s_1)|_{s_1=t(d)+1}^{s-1}\} \\ \quad\quad +{\rm Proj}\{{ u}(t(d)+k)|\tilde{\cal Y}_1(s)\} \\ \quad =\hat{{ u}}(t(d)+k|s-1,1) \\ \quad\quad +\langle{ u}(t(d)+k),\tilde{\cal Y}_1(s)\rangle Q_{\tilde{\cal Y}_1}^{-}(s)\tilde{\cal Y}_1(s) \\ \quad =\hat{{ u}}(t(d)+k|s-1,1) \\ \quad\quad +G(t(d)+k,s,1)Q_{\tilde{\cal Y}_1}^{-}(s)\tilde{\cal Y}_1(s), $ | (25) |
let $s=t(d)+k$,then
| $ \hat{{ u}}(t(d)+k|t(d)+k,1) \\ \quad =\hat{{ u}}(t(d)+k|t(d)+k-1,1)+G(t(d) \\ \quad\quad +k,t(d)+k,1) Q_{\tilde{\cal Y}_1}^{-}(t(d)+k)\tilde{\cal Y}_1(t(d)+k),~~\label{e3.63} $ | (26) |
since
$ \hat{{ u}}(t(d)+k|t(d)+k-1,1)\in {\cal L}(\tilde{\cal Y}_2(s)|_{s=0}^{t(d)};\tilde{\cal Y}_1(s)|_{s=t(d)+1}^{t(d)+k-1}), $and
| $ {e_1}(t(d) + k,1) \bot L({\widetilde Y_2}(s)|_{s = 0}^{t(d)};{\widetilde Y_1}(s)|_{s = t(d) + 1}^{t(d) + k - 1}), $ |
that is
| $ {e_1}(t(d)+k,1)\perp \hat{{ u}}(t(d)+k|t(d)+k-1,1), $ |
so
| $ \langle{ e}_1(t(d)+k,1),\hat{{ u}}(t(d)+k|t(d)+k,1)\rangle \\ \quad =\langle{ e}_1(t(d)+k,1),\hat{{ u}}(t(d)+k|t(d)+k-1,1) \\ \quad\quad +G(t(d)+k,t(d)+k,1) \\ \quad\quad \times Q_{\tilde{\cal Y}_1}^{-}(t(d)+k)\tilde{\cal Y}_1(t(d)+k)\rangle\\ \quad= \langle{ e}_1(t(d)+k,1),\hat{{ u}}(t(d)+k|t(d)+k-1,1)\rangle\\ \quad\quad +\langle{ e}_1(t(d)+k,1),G(t(d)+k,t(d)+k,1) \\ \quad\quad \times Q_{\tilde{\cal Y}_1}^{-}(t(d)+k)\tilde{\cal Y}_1(t(d)+k)\rangle \\ \quad = \langle{ e}_1(t(d)+k,1),G(t(d)+k,t(d)+k,1) \\ \quad\quad \times Q_{\tilde{\cal Y}_1}^{-}(t(d)+k) \\ \quad\quad \times [{\cal C}_{11}{ e}_1(t(d)+k,1)\\ \quad\quad + D_1{ w}(t(d)+k){ x}_1(t(d)+k) \\ \quad\quad + {\tilde{{\bar{\cal V}}}}_1(t(d)+k,1)]\rangle.\label{e3.64} $ | (27) |
Since
| $ {\tilde{{\bar{\cal V}}}}_1(t(d)+k)={{\bar{\cal V}}}_1(t(d)+k)-{\hat{{\bar{\cal V}}}}_1(t(d)+k,1),\\ { e}_1(t(d)+k,1)\perp {\hat{{\bar{\cal V}}}}_1(t(d)+k,1) $ |
and
| $ \langle{ e}_1(t(d)+k,1),{{\bar{\cal V}}}_1(t(d)+k,1)\rangle\\ \qquad =H_1^{\rm T}(t(d)+k,t(d)+k,1), $ |
so (27) can be rewritten as
| $ \begin{array}{l} \langle {e_1}(t(d) + k,1),\widehat u(t(d) + k|t(d) + k,1)\rangle \;\\ \; = \langle {e_1}(t(d) + k,1),G(t(d) + k,t(d) + k,1)Q_{{{\widetilde Y}_1}}^ - (t(d) + k)\\ \times \left[ {{C_{11}}{e_1}(t(d) + k,1) + {D_1}w(t(d) + k){x_1}(t(d) + k)} \right.\\ + \left. {{{\widetilde {\overline V }}_1}(t(d) + k)} \right]\rangle \quad \\ = \left[ {{P_1}(t(d) + k,1)C_{11}^{\rm{T}} + H_1^{\rm{T}}(t(d) + k,t(d) + k,1)} \right]\\ \times Q_{{{\widetilde Y}_1}}^ - (t(d) + k){G^{\rm{T}}}(t(d) + k,t(d) + k,1)\\ = L(t(d) + k,t(d) + k,1)Q_{{{\widetilde Y}_1}}^ - (t(d) + k)\\ \times {G^{\rm{T}}}(t(d) + k,t(d) + k,1)\\ = K(t(d) + k,1){G^{\rm{T}}}(t(d) + k,t(d) + k,1). \end{array} $ | (28) |
In addition,since $\langle\hat{ u}(t(d)+k|t(d)+k,1),\tilde{ u}(t(d)+k|t(d)+k,1)\rangle=0$,
| $ -\langle{ u}(t(d)+k),\hat{ u}(t(d)+k|t(d)+k,1)\rangle \\ \quad\quad +\langle\hat{ u}(t(d)+k|t(d)+k,1),\hat{ u}(t(d)+k|t(d)+k,1)\rangle \\ \quad\quad -\langle\hat{ u}(t(d)+k|t(d)+k,1),{ u}(t(d)+k)\rangle \\ \quad =-\langle{ u}(t(d)+k),\hat{ u}(t(d)+k|t(d)+k,1)\rangle \\ \quad\quad +\langle\hat{ u}(t(d)+k|t(d)+k,1),\hat{ u}(t(d)+k|t(d)+k,1)\rangle\\ \quad\quad -\langle\hat{ u}(t(d)+k|t(d)+k,1),\hat{ u}(t(d)+k|t(d)+k,1) \\ \quad\quad +\tilde{ u}(t(d)+k|t(d)+k,1)\rangle \\ \quad =-\langle{ u}(t(d)+k),\hat{ u}(t(d)+k|t(d)+k,1)\rangle \\ \quad =-G_3(t(d)+k,t(d)+k|t(d)+k,1).\label{e3.66} $ | (29) |
Thus,from (24),(28) and (29),the main Riccati equation can be yielded as
| $ P_1(t(d)+k+1,1)\\ \quad =A_1P_1(t(d)+k,1)A_1^{\rm T}\\ \quad\quad +A_1\left[G_1^{\rm T}(t(d)+k,t(d)+k,1)-K(t(d)+k,1)\right. \\ \quad\quad \times\left. G^{\rm T}(t(d)+k,t(d)+k,1)\right]B_1^{\rm T} \\ \quad\quad +B_1\left[G_1(t(d)+k,t(d)+k,1)\right. \\ \quad\quad - \left.G(t(d)+k,t(d)+k,1)K^{\rm T}(t(d)+k,1)\right]A_1^{\rm T}\\ \quad\quad +B_1[Q_u-G_3(t(d)+k,t(d)+k|t(d)+k,1)]B_1^{\rm T} \\ \quad\quad -A_1K(t(d)+k,1)Q_{\tilde{\cal Y}_1}(t(d)+k) \\ \quad\quad \times K^{\rm T}(t(d)+k,1)A_1^{\rm T},\qquad k=1,...,d-1,~\label{e3.53} $ | (30) |
where $\{G,G_1,G_3,H_1,H_2\}(t(d)+k,\cdot,1)$ are given in Lemma 3.3
in
In this part,based on the error covariance matrix $P_1(t,2)$ and $P_1(t(d)+k,1)$,we will give the Kalman filter for ${x}_1(t)$.
$\hat{ x}_1(t+1|t,2)$ can be given by traditional Kalman filtering as
| $ \hat{ x}_1(t+1,2)=A_1\hat{ x}_1(t,2)+A_1K(t,2) \\ \quad \times\left[{\cal Y}_2(t)-{\cal C}_{12}\hat{ x}_1(t,2)-{\hat{\bar{\cal V}}}_2(t,2)\right]+B_1\hat{ u}(t|t,2), \\ \hat{ x}_1(0,2)=\hat{ x}_1(0|-1,2)=0,~~~\label{e3.67} $ | (31) |
where
| $ \begin{array}{l} \widehat u(t|t,2) = \widehat u(t|t - 1,2) + G(t,t,2)Q_{{{\widetilde Y}_2}}^ - (t)\quad \\ \times \left[{{Y_2}(t) - {C_{12}}{{\hat x}_1}(t,2) - {{\widehat {\overline V }}_2}(t,2)} \right],\\ \widehat u(0| - 1,2) = 0, \end{array} $ | (32) |
| $ {\hat{\bar{\cal V}}}_2(t,2)={\hat{\bar{\cal V}}}_2(t|t-1,2) \\ \quad ={\hat{\bar{\cal V}}}_2(t|t-2,2)+H(t,t-1,2)Q_{\tilde{\cal Y}_2}^{-}(t-1)\\ \quad\quad \times\left[{\cal Y}_2(t-1)-{\cal C}_{12}\hat{ x}_1(t-1,2)-{\hat{\bar{\cal V}}}_2(t-1,2)\right],\\ {\hat{\bar{\cal V}}}_2(0,2)=0.~~\label{e3.69} $ | (33) |
$\hat{ x}_1(t+1|t+1,1)$ can be given as follows.
Theorem 1. Under Assumptions 1 and 2,for the singular system model (1)-(3) and the corresponding restricted equivalent delayed system model (4)-(6),Kalman filter $\hat{ x}_1(t(d)$ $+$ $k + 1|t(d)+k+1,1)$ can be given as
| $ \hat{ x}_1(t(d)+k+1|t(d)+k+1,1) \\ \quad =\hat{ x}_1(t(d)+k+1,1)+K(t(d)+k+1,1) \\ \quad\quad \times\Big[{\cal Y}_1(t(d)+k+1)-{\cal C}_{11}\hat{ x}_1(t(d)+k+1,1)\\ \quad\quad -{\hat{\bar{\cal V}}}_1(t(d)+k+1,1)\Big],\label{e3.70} $ | (34) |
where
| $ \hat{ x}_1(t(d)+k+1,1) \\ \quad =A_1\hat{ x}_1(t(d)+k,1)+A_1K(t(d)+k,1) \\ \quad\quad \times\Big[{\cal Y}_1(t(d)+k)-{\cal C}_{11}\hat{ x}_1(t(d)+k,1) \\ \quad\quad -{\hat{\bar{\cal V}}}_1(t(d)+k,1)\Big]\notag\\ \quad\quad +B_1\hat{ u}(t(d)+k|t(d)+k,1),\\ {\hat{ x}}_1(t(d)+1,1)=\hat{ x}_1(t(d)+1,2),\\ \qquad\qquad\qquad\qquad\qquad\qquad k=0,...,d-1,\label{e3.71} $ | (35) |
and
| $ \hat{{ u}}(t(d)+k|t(d)+k,1) \\ \quad =\hat{{ u}}(t(d)+k|t(d)+k-1,1) \\ \quad\quad +G(t(d)+k,t(d)+k,1)Q_{\tilde{\cal Y}_1}^{-}(t(d)+k) \\ \quad\quad \times\Big[{\cal Y}_1(t(d)+k)-{\cal C}_{11}\hat{ x}_1(t(d)+k,1) \\ \quad\quad -{\hat{\bar{\cal V}}}_1(t(d)+k,1)\Big],\\ \hat{ u}(t(d)+1,1)=\hat{ u}(t(d)+1,2),~\label{e3.72} $ | (36) |
| $ {\hat{\bar{\cal V}}}_1(t(d)+k|t(d)+k-1,1) \\ \quad ={\hat{\bar{\cal V}}}_1(t(d)+k|t(d)+k-2,1) \\ \quad\quad +H(t(d)+k,t(d)+k-1,1)Q_{\tilde{\cal Y}_1}^{-}(t(d)+k-1) \\ \quad\quad \times \Big[{\cal Y}_1(t(d)+k-1)-{\cal C}_{11}\hat{ x}_1(t(d)+k-1,1) \\ \quad\quad - {\hat{\bar{\cal V}}}_1(t(d)+k-1,1)\Big],\\ {\hat{\bar{\cal V}}}_1(t(d)+1,1)={\hat{\bar{\cal V}}}_1(t(d)+1,2),\notag\\ {\hat{\bar{\cal V}}}_1(t(d)+1,2) \\ \quad ={\hat{\bar{\cal V}}}_1(t(d)+1|t(d)-1,2) \\ \quad\quad +H(t(d)+1,t(d),12)Q_{\tilde{\cal Y}_2}^{-}(t(d)) \quad\quad \times\left[{\cal Y}_2(t(d))-{\cal C}_{12}\hat{ x}_1(t(d),2) -{\hat{\bar{\cal V}}}_2(t(d),2)\right],~\label{e3.73a} $ | (37) |
$K(t(d)+k,1)$ is as in (22),$\hat{ x}_1(t(d)+1,2)$ is from
(31),$\{G,$ $H\}(t(d)+k,~\cdot,~1),~H(t(d)+1,t(d),12)$ are as in
Lemma 3.4 in
Proof.~From the projection theorem,we have
| $ \hat{ x}_1(t(d)+k+1|t(d)+k+1,1) \\ \quad = {\rm Proj}\left\{{ x}_1(t(d)+k+1)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)}; \tilde{\cal Y}_1(s)|_{s=t(d)+1}^{t(d)+k+1}\right\} \\ \quad =\hat{ x}_1(t(d)+k+1,1) \\ \quad\quad +{\rm Proj}\left\{{ x}_1(t(d)+k+1)|\tilde{\cal Y}_1(t(d)+k+1)\right\} \\ \quad =\hat{ x}_1(t(d)+k+1,1) \\ \quad\quad +\langle{ x}_1(t(d)+k+1),\tilde{\cal Y}_1(t(d)+k+1)\rangle \\ \quad\quad \times Q_{\tilde{\cal Y}_1}^{-}(t(d)+k+1)\tilde{\cal Y}_1(t(d)+k+1) \\ \quad =\hat{ x}_1(t(d)+k+1,1) \\ \quad\quad + K(t(d)+k+1,1)\tilde{\cal Y}_1(t(d)+k+1),\label{e3.74} $ | (38) |
combining (39) with (15) yields (34).
From (21) and (15),
| $ \hat{ x}_1(t(d)+k+1,1) \\ \quad =A_1\hat{ x}_1(t(d)+k,1) \\ \quad\quad +A_1K(t(d)+k,1)\tilde{\cal Y}_1(t(d)+k) \\ \quad\quad +B_1\hat{ u}(t(d)+k|t(d)+k,1) \\ \quad = A_1\hat{ x}_1(t(d)+k,1)+B_1\hat{ u}(t(d)+k|t(d)+k,1)\\ \quad\quad +A_1K(t(d)+k,1)\Big[{\cal Y}_1(t(d)+k) \\ \quad\quad -{\cal C}_{11}{\hat{ x}}_1(t(d)+k,1)-{\hat{\bar{\cal V}}_1}(t(d)+k,1)\Big], $ | (39) |
which is (35).
From (26) and (15),
| $ \hat{{ u}}(t(d)+k|t(d)+k,1) \\ \quad =\hat{{ u}}(t(d)+k|t(d)+k-1,1) \\ \quad\quad +G(t(d)+k,t(d)+k,1) \\ \quad\quad \times Q_{\tilde{\cal Y}_1}^{-}(t(d)+k)\tilde{\cal Y}_1(t(d)+k)\\ \quad =\hat{{ u}}(t(d)+k|t(d)+k-1,1) \\ \quad\quad +G(t(d)+k,t(d)+k,1)Q_{\tilde{\cal Y}_1}^{-}(t(d)+k) \\ \quad\quad \times\Big[{\cal Y}_1(t(d)+k)-{\cal C}_{11}\hat{ x}_1(t(d)+k,1) \\ \quad\quad -{\hat{\bar{\cal V}}}_1(t(d)+k,1)\Big],\label{e3.76} $ | (40) |
which is (36).
From the projection theorem,we have
| $ \begin{array}{l} {\widehat {\overline V }_1}(t(d) + k|s,1) = \\ \;\;\;{\rm{Proj}}\{ {\overline V _1}(t(d) + k)|{\widetilde Y_2}(s)|_{s = 0}^{t(d)};\quad \\ \;\;\;\;{\widetilde Y_1}(s)|_{s = t(d) + 1}^s\} \\ = {\rm{Proj}}\{ {\overline V _1}(t(d) + k)|{\widetilde Y_2}(s)|_{s = 0}^{t(d)};\quad \\ \;\;\;\;\;{\widetilde Y_1}(s)|_{s = t(d) + 1}^{s - 1}\} \quad \\ \;\;\;\;\; + {\rm{Proj}}\{ {\overline V _1}(t(d) + k)|{\widetilde Y_1}(s)\} = \\ \;\;\;\;\;{\widehat {\overline V }_1}(t(d) + k|s - 1,1)\\ \;\;\;\; + \langle {\overline V _1}(t(d) + k),{\widetilde Y_1}(s)\rangle Q_{{{\widetilde Y}_1}}^ - (s){\widetilde Y_1}(s)\\ \;\;\;\;\;\; = {\widehat {\overline V }_1}(t(d) + k|s - 1,1)\\ \;\;\;\;\; + H(t(d) + k,s,1)Q_{{{\widetilde Y}_1}}^ - (s){\widetilde Y_1}(s), \end{array} $ | (41) |
then combine (42) with (15),(37) can be given when $s=t(d)$ $+$ $k-1$.
Similarly,
| $ {\hat{\bar{\cal V}}}_1(t(d)+1,2) \\ \quad ={\rm Proj}\left\{\bar{\cal V}_1(t(d)+1)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)}\right\} \\ \quad ={\rm Proj}\left\{\bar{\cal V}_1(t(d)+1)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)-1}\right\} \\ \quad\quad +{\rm Proj}\left\{{\bar{\cal V}}_1(t(d)+1)|\tilde{\cal Y}_2(t(d))\right\} \\ \quad ={\hat{\bar{\cal V}}}_1(t(d)+1|t(d)-1,2) \\ \quad\quad +H(t(d)+1,t(d),12)Q_{\tilde{\cal Y}_2}^{-}(t(d)) \\ \quad\quad \times \left[{\cal Y}_2(t(d))-{\cal C}_{12}\hat{ x}_1(t(d),2) -{\hat{\bar{\cal V}}}_2(t(d),2)\right],~~\label{e3.77a} $ | (42) |
which is (38),then the proof is over.
F.Kalman Filter for ${ x_2(t)}$Kalman filter $\hat{ x}_2(t|t)$ for the second restricted state variable can be given as in Theorem 2.
Theorem 2. Given the initial value for the system model (5)-(7) with ${ x}_2(0)=-\sum_{j=0}^{\lambda-1}F_1^jB_2{ u}(j)$,$\hat{ x}_2(t|t)=\hat{ x}_2(t|t,1)$ can be given as
| $ \hat{ x}_2(t|t,1)=-\sum_{j=0}^{\lambda-1}F_1^jB_2\hat{ u}(t+j|t,1),~\label{e3.94} $ | (43) |
where
| $ \hat{ u}(t+j|t,1)=\hat{ u}(t+j|t-1,1) \\ \quad\ + G(t+j,t,1)Q_{\tilde{\cal Y}_1}^{-}(t)\tilde{\cal Y}_1(t),\label{e3.95} $ | (44) |
with $\hat{ u}(t+j|t(d),1)=\hat{ u}(t+j|t(d),2)$ being given as
| $ \hat{ u}(t+j|t(d),2)=\hat{ u}(t+j|t(d)-1,2) \\ \quad\ +G(t+j,t(d),2)Q_{\tilde{\cal Y}_2}^{-}(t(d)) \tilde{\cal Y}_2(t(d)),\label{e3.95a} $ | (45) |
with
| $ {\tilde{\cal Y}}_i(t)={\cal Y}_i(t)-{\cal C}_{1i}{\hat{ x}}_1(t,i)+{\hat{\bar{\cal V}}}_i(t,i),~~i=1,2,~\label{e3.96} $ | (46) |
and $\hat{ x}_1(t,1)$ is from (35),and $\hat{ x}_1(t(d),2)$ is from (31).
Proof. Similar to the above projection formulae and (13),we have
| $ \hat{ x}_2(t|t,1)={\rm Proj}\left\{{ x}_2(t)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)}; \tilde{\cal Y}_1(s)|_{s=t(d)+1}^{t}\right\}\\ \quad ={\rm Proj}\Big\{-\sum_{j=0}^{\lambda-1}F_1^jB_2{ u}(t+j)|\tilde{\cal Y}_2(s)|_{s=0}^{t(d)}; \\ \quad\quad \tilde{\cal Y}_1(s)|_{s=t(d)+1}^{t}\Big\} \\ \quad =-\sum_{j=0}^{\lambda-1}F_1^jB_2\hat{ u}(t+j|t,1),\label{e3.97} $ | (47) |
which is (44).
(45) can be obtained from (25),(46) can be obtained similar to (45),and (47) can be obtained from (15).
G.Main ResultsHaving given Kalman filters $\hat{ x}_1(t|t,1)$ and $\hat{ x}_2(t|t,1)$,Kalman filter for the delayed singular system corrupted by multiplicative noises will be proposed without proof,
Theorem 3. For (1)-(3) under Assumptions 1 and 2,if the initial condition $[{0 \ I}]J_2^{-1}{ x}(0)= -\sum_{j=0}^{\lambda-1}F_1^jB_2{ u}(j)$ or ${ x}_2(0)$ $=$ $-\sum_{j=0}^{\lambda-1}F_1^jB_2{ u}(j)$ is satisfied,then Kalman filter $\hat{ x}(t|t)=$ $\hat{ x}(t|t,1)$ can be given by
| $ \hat{ x}(t|t)=J_2\left[\begin{array}{*{20}c}\hat{ x}_1(t|t,1)\\ \hat{ x}_2(t|t,1)\end{array}\right],\label{e3.98} $ | (48) |
where $\hat{ x}_1(t|t,1)$ is from (34),$\hat{ x}_2(t|t,1)$ is from (44).
IV.NUMERICAL EXAMPLEIn this part,a numerical example of petroleum seismic exploration
will be given. As is well known,during the process of petroleum
seismic exploration,there exist many uncertain factors,such as
time-variant,uncertainties,the spreading loss,transmission of
the source wavelet,and so on. So,only additive noise can not
describe this case,so we use multiplicative noise in the system
model to simulate this case. In addition,in this paper,to show
the comparison between Kalman filter and the multiple-step
predictor,the system model is same as in
| $ {J_1} = \left[{\begin{array}{*{20}{c}} 0&1&0\\ 1&{ - 1}&0\\ 0&0&2 \end{array}} \right],{J_2} = \left[{\begin{array}{*{20}{c}} 1&0&0\\ 1&1&0\\ 0&0&1 \end{array}} \right], $ | (49) |
and
| $ \begin{array}{l} {A_1} = \left[ {\begin{array}{*{20}{c}} {0.4}&0\\ 0&{ - 0.4} \end{array}} \right],{B_1} = \left[ {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]\\ N = 0,{F_1} = 0,\lambda = 1,{B_2} = 4,\\ {C_1} = \left[ {\begin{array}{*{20}{c}} {2\;\;\;\;1} \end{array}} \right],{C_2} = 1,{C_{1d}} = \left[ {3\;\;\;\;\;2} \right],{C_{2d}} = 1,\\ {D_1} = \left[ {\begin{array}{*{20}{c}} 3&2 \end{array}} \right],{D_2} = 2,{D_{1d}} = \left[ {3\;\;\;\;\;\;1} \right],{D_{2d}} = 1. \end{array} $ |
Computing as in Theorems 1-3,we have
| $ \hat{ x}(t|t)=J_2 \left[\begin{array}{*{20}c}\hat{ x}_1(t|t,1)\\ \hat{ x}_2(t|t,1)\end{array}\right] \\[1mm] \quad =\left[\begin{array}{*{20}c}\hat{ x}_{11}(t|t,1) \\ \hat{ x}_{11}(t|t,1)+\hat{ x}_{12}(t|t,1)\\ \hat{ x}_2(t|t,1)\end{array}\right]=\left[\begin{array}{*{20}c}\hat{ x}_{F}(t|t)\\ \hat{ x}_{S}(t|t)\\\hat{ x}_T(t|t)\end{array}\right], $ | (50) |
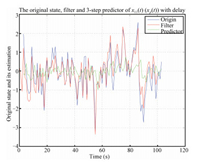
then the origin,its optimal filter $\hat{ x}(t|t)$ and 3-step
predictor $\hat{ x}(t$ $+$ $3|t)$ can be drawn,the first
sub-state filter $\hat{ x}_{F}(t|t)=\hat{ x}_{11}(t|t,$ $1)$
and predictor $\hat{ x}_{F}(t+3|t)=\hat{ x}_{11}(t+3|t,1)$
are as in
|
Download:
|
| Fig. 1 The original state,its filter and 3-step predictor for the first state of x(t). | |
|
Download:
|
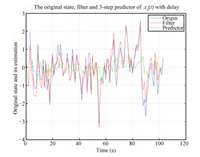
| Fig. 2 The original state and its filter for the second state of x(t). | |

|
Download:
|
| Fig. 3 The original state and its filter for the third state of x(t). | |
From Figs. 1-3,the optimal filters $\hat{ x}_{F}(t|t)$,
$\hat{ x}_{S}(t|t)$,$\hat{ x}_{T}(t|t)$ of $\hat{
x}(t|t)$ for the original system (1)-(3) can give good estimation,
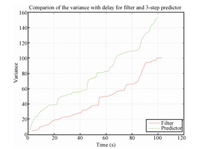
and they are better than the 3-step predictor,which can also be
verified in
|
Download:
|
| Fig. 4 The comparison between the filter error variance and 3-step predictor. | |
Kalman filtering problem for discrete-time singular system corrupted
by multiplicative noises is dealt with,and the system model
includes two measurements,one of which is delayed measurement. By
utilizing the method of singular value decomposition and the method
of re-organization of innovation analysis lemma,Kalman filters and
the corresponding filters for the restricted equivalent delayed
system and the original singular system are given. The proposed
Kalman filtering result extends the series of the estimation for
singular system with multiplicative noises and delayed
measurement
[14, 15, 16, 20],where
| [1] | Wiener N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series. Cambridge, MA:The MIT Press, 1949. |
| [2] | Kalman R E. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 1960, 82(1):35-45 |
| [3] | Hassibi B, Sayed A H, Kailath T. Linear estimation in Krein spaces. I. Theory. IEEE Transactions on Automatic Control, 1996, 41(1):18-33 |
| [4] | Hassibi B, Sayed A H, Kailath T. Linear estimation in Krein spaces. II. Applications. IEEE Transactions on Automatic Control, 1996, 41(1):34-49 |
| [5] | Hassibi B, Sayed A H, Kailath T. Indefinite-Quadratic Estimation and Control-A Unified Approach to H2 and H∞ Theories. Englewood Cliffs, NJ:Prentice-Hall, 1999. |
| [6] | Zhang H S, Xie L H, Soh Y C. A unified approach to linear estimation for discrete-time systems. II. H∞ estimation. In:Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, FL:IEEE, 2001. 2923-2928 |
| [7] | Zhang H S, Xie L H, Soh Y C. Risk-sensitive filtering, prediction and smoothing for discrete-time singular systems. Automatica, 2003, 39(1):57-66 |
| [8] | Zhang H S, Chai T Y, Liu X J. A unified approach to optimal state estimation for stochastic singular systems. Automatica, 1998, 34(6):777-781 |
| [9] | Dai L. Filtering and LQG problems for discrete-time stochastic singular systems. IEEE Transactions on Automatic Control, 1989, 34(10):1105-1108 |
| [10] | Olemskoi A I. Theory of stochastic systems with singular multiplicative noise. Physics-Uspekhi, 2007, 41(3):269 |
| [11] | Chu D S, Gao S W, Guo L. An augmented optimal filter for multichannel stochastic singular systems with multiplicative noise. In:Proceedings of the 2007 IEEE International Conference on Automation and Logistics. Jinan, China:IEEE, 2007.378-382 |
| [12] | Chu D S, Gao S W. State optimal estimation algorithm for singular systems with multiplicative noise. Periodical of Ocean University of China, 2008, 38(5):814-818(in Chinese) |
| [13] | Gao S W. Study of optimal estimation algorithm for singular systems with multiplicative noise[Master dissertation], Ocean University of China, China, 2008(in Chinese) |
| [14] | Lu X, Wang H X, Wu F. Optimal multi-step predictor for descriptor systems with multiplicative noise and delayed measurement. Control Theory and Applications, 2015, 32(6):787-793(in Chinese) |
| [15] | Lu X, Wang L L, Wang H X, Pu Q, Dong X. Optimal FSL smoothing for delayed descriptor systems. In:Proceedings of the 34th Chinese Control Conference. Hangzhou, China:IEEE, 2015. 131-134 |
| [16] | Lu X, Dong X, Wang H X, Song B Y. On fixed-point smoothing for descriptor systems with multiplicative noise and single delayed observations. Mathematical Problems in Engineering, 2015, 2015:Article ID 658153 |
| [17] | Ni Y H, Li X. Consensus seeking in multi-agent systems with multiplicative measurement noises. Systems and Control Letters, 2013, 62(5):430-437 |
| [18] | Zhang H S, Xie L H, Zhang H S, Soh Y C. A reorganized innovation approach to linear estimation. IEEE Transactions on Automatic Control, 2004, 49(10):1810-1814 |
| [19] | Lu X, Liu S, Luan S, Pu Q. Kalman filtering for singular WSN systems with multiplicative noise. In:Proceedings of the 2014 International Conference on Mechatronics and Control. Jinzhou, China:IEEE, 2014. 1319-1323 |
| [20] | Lu X, Dong X, Wang H X. Optimal fixed-point smoothing for delayed descriptor systems with multiplicative noise. In:Proceedings of the 27th Chinese Control and Decision Conference. Qingdao, China:IEEE, 2015.2810-2813 |
 2016, Vol.3
2016, Vol.3 


