2. Hefei University of Technology, Hefei 230009, China, and also with Georgia Institute of Technology, GA 30332, USA;
3. Georgia Institute of Technology, GA 30332, USA
I. INTRODUCTION
In order to control the constrained discrete mechanical system, the dynamic model should first be obtained. Obtaining equations of motion for constrained discrete mechanical systems is one of the central issues in multi-body dynamics. The problem has been energetically and continuously worked on by many scientists, engineers and mathematicians since constrained motion was initially described by Lagrange[1]. He invented the special Lagrange multiplier method to deal with constrained motion. However, the Lagrange multiplier method relies on problem-specific approaches to the determination of the multipliers and it is often very difficult to find the multipliers to obtain the explicit equations of motion for systems which have large number of degrees of freedom and a mass of non-integrable constraints. Gauss[2] introduced a general, new principle of mechanics for handling constrained motion. Gauss's principle gives a clear description of the general nature of constrained motion in terms of the minimization of a function of the accelerations of the particles of a system. Formulations of the equations of constrained motion, when the constraints satisfy D'Alember's principle, were independently offered by Gibbs[3] and Appell[4]. Pars[5] in his treatise on the analytical dynamics refers to the Gibbs-Appell equations as "probably the most comprehensive equations of motion so far discovered". But Gibbs-Appell equations require a felicitous choice of problem-specific quasi-coordinates and suffer from similar problems in dealing with systems with a large number of degrees of freedom and many non-integrable constraints. Dirac[6] developed, using Poisson brackets, a recursive scheme for determining the Lagrange multipliers for singular, Hamiltonian systems where the constraints do not exactly depend on time.
Udwadia and Kalaba[7, 8] obtained a concise, explicit set of equations of motion for constrained discrete dynamical systems which lead to a simple and new fundamental view of Lagrangian mechanics. They derived the fundamental equation of motion that describes the dynamics of constrained systems derived from Gauss's principle which seems somewhat less popular than the principles of Lagrange, Hamilton, Gibbs, and Appell. The equations can deal with holonomic and also non-holonomic constraints. Udwadia and Kalaba[9, 10] observed that all the above researches have used D'Alember's principle as their starting point which indicates that the forces of constraints are considered to be ideal and the total work done by the forces of constraints under virtual displacement is always zero. This assumption works well in many situations and is regarded as the core of classical analytical dynamics, but it is not applicable when the constraints are nonideal. Thus, Udwadia and Kalaba generalized their previous equations to constrained mechanical systems that may not satisfy D'Alember's principle.
In this paper, we use fundamental equation of constrained system proposed by Udwadia and Kalaba to get the dynamic equations of motion of the constrained mechanical system. According to this approach, the unconstrained system is first considered whose equations of motion can be obtained by Lagrangian mechanics in terms of the generalized coordinates. Then constraint equations are written in the form of second order equation. The dynamic equations can be obtained by imposing the additional generalized forces of constraint obtained from the second order constraint equations upon the unconstrained system. Based on the obtained dynamic model, constraint-following servo control is used to realize the performance requirement modeled as servo constraints (also called active constraints, program constraints or prescribed constraints). That is to use a set of servo controls to generate the appropriate constraint force for the system to obey the constraints.
We know, Newton-Euler mechanics divides forces into internal and external force and the motion is structureless. While analytical mechanics divides forces into impressed (or given) and constraints. The motion is under constraints and hence has a structure. As illustrated above, over the past century and a half, key developments in Lagrangian mechanics include the Maggi equation[11, 12], the Boltzmann and Hamel equation[12, 13, 14], the Gibbs and Appell equation [3, 4, 5, 14], and the Udwadia and Kalaba equation[8]. However, the emphasis of all these developments mainly falls into the passive constraint (also called material constraint) problem in which the constraint is followed in a passive manner. That is, as the constraint is determined, the environment (such as the structure of the machine) can generate the required constraint force automatically. Taking a particle constrained to move on a table surface as an example, the table surface can automatically generate the constraint force to support the particle. One is not necessary to consider how to generate the constraint force. So, the generation of constraint force is often considered to be a design task: design the machine structure to generate the constraint force automatically.
We consider the issue of generation of constraint forces as a control task (that is servo constraint problem), rather than a design task. The servo constraint problem has rarely been studied in analytical mechanics. Perhaps because the concept of servos is relatively new in analytical mechanics. The past efforts on this problem focused on individual examples (e.g., [15, 16]) rather than systematic framework. In the article of Chen[17], a systematic approach for the servo constraint problem is proposed. A system is equipped with a set of servo controls to provide the required constraint force. Then, the system obeys a set of required constraints. Through the use of servo controls, the constraint force is generated, not through the passive environment.
The main contributions of this paper are fivefold. First, Udwadia-Kalaba approach is described in detail. The procedure of obtaining fundamental equation of constrained motion is shown. Second, based on the dynamic model obtained by Udwadia-Kalaba approach, constraint-following servo control is proposed to realize the performance requirement modeled as servo constraints. Third, the inverse dynamics control problem based on Moore-Penrose generalized inverse, second-order constraints and constraint violation suppression utilized in the proposed approach are explained. Fourth, the approach is novel and systematic. It is applicable to not only fully actuated but also underactuated and redundantly actuated mechanical systems. Fifth, two-mass spring system and coordinated robot system are presented as examples to specifically illustrate the approach incorporating Udwadia-Kalaba approach and constraint-following servo control.
A. Fundamental Equation of Constrained Systems
According to Udwadia-Kalaba approach, first we should consider an unconstrained discrete dynamical system whose configuration is described by the $n$ generalized coordinates $q := [q_1, q_2, \ldots, q_n]^{\rm T}$. Its equation of motion can be obtained, using Newtonian or Lagrangian mechanics, by the relation
| \begin{equation} M(q, t)\ddot q=Q(q, \dot q, t), \end{equation} | (1) |
| \begin{equation}\label{2.2} \ddot q=M^{-1}(q, t)Q(q, \dot q, t)=a(q, \dot q, t). \end{equation} | (2) |
Second, constraints present in the system should be considered. We shall assume that the system is subjected to $h$ holonomic constraints of the form
| \begin{equation}\label{2.3} \varphi_i (q, t)=0, \qquad i=1, 2, \ldots, h, \end{equation} | (3) |
| \begin{equation}\label{2.4} \varphi_i (q, \dot q, t)=0, \qquad i=h+1, h+2, \ldots, m. \end{equation} | (4) |
We can get the differentiation of the usual constraint equations in Lagrangian mechanics which are usually in Pfaffian form, that is to say, under the assumption of sufficient smoothness, take time derivative once on non-holonomic constraints and twice on holonomic constraints, then it will provide the constraint equations in the matrix form:
| \begin{equation}\label{2.5} \hat A(q, \dot q, t)=\hat b(q, \dot q, t), \end{equation} | (5) |
The final step is to form the explicit equations of motion with constraints. Due to the presence of constraints, additional "generalized forces of constraints" should be imposed on the system. So, the actual explicit equation of motion of the constrained system could be assumed to take the form:
| \begin{equation}\label{2.6} M(q, t)\ddot q=Q(q, \dot q, t)+Q^c(q, \dot q, t), \end{equation} | (6) |
| \begin{equation}\label{2.7} Q^c(q, \dot q, t)=Q^c_{id}(q, \dot q, t)+Q^c_{nid}(q, \dot q, t), \end{equation} | (7) |
Udwadia and Kalaba generalize D'Alember's principle to include forces of constraint that may do positive, negative, or zero work under virtual displacement at any instant of time during the motion of the constrained system, that is to say, they extend the Lagrange's form of D'Alember's principle to include nonideal constraints. Now, we denote constraint force as $c(q, \dot q, t)\in \textbf{R}^n$. The constraint force does the work $W=v^{\rm T}c$ (the same as the work done by $Q^c(q, \dot q, t)$ in any displacement $v$ which subjects to $\hat A(q, \dot q, t)v=0$. So we write it down in the form of (we will omit arguments of functions where no confusions may arise from now on)
| \begin{equation}\label{2.8} W=v^{\rm T}Q^c=v^{\rm T}c, \end{equation} | (8) |
| \begin{equation}\label{2.9} v^{\rm T}Q^c_{id}=0, \end{equation} | (9) |
| \begin{equation}\label{2.10} v^{\rm T}Q^c_{nid}\neq0, \end{equation} | (10) |
Udwadia and Kalaba have proved that the ideal constraint force takes the form
| \begin{equation}\label{2.11} Q^c_{id}=M^{\frac{1}{2}}{\hat B}^+(\hat b-\hat AM^{-1}Q), \end{equation} | (11) |
| \begin{equation}\label{2.12} Q^c_{nid}=M^{\frac{1}{2}}(I-{\hat B}^+\hat B)M^{-\frac{1}{2}}c, \end{equation} | (12) |
From (6), (7), (11) and (12), the explicit equation of motion that governs the evolution of the constrained system (including both ideal and nonideal constraints) is
| \begin{equation}\label{2.13} M\ddot q=Q+M^{\frac{1}{2}}{\hat B}^+(\hat b-\hat AM^{-1}Q)+M^{\frac{1}{2}}(I-{\hat B}^+\hat B)M^{-\frac{1}{2}}c, \end{equation} | (13) |
When $c$ is always zero, (13) reduces to the D'Alember's principle, which means the total work done under virtual displacement is zero, the constraints are ideal, the constraint force is
| \begin{equation}\label{2.14} Q^c=Q^c_{id}=M^{\frac{1}{2}}{\hat B}^+(\hat b-\hat AM^{-1}Q), \end{equation} | (14) |
| \begin{equation}\label{2.15} M\ddot q=Q+M^{\frac{1}{2}}{\hat B}^+(\hat b-\hat AM^{-1}Q), \end{equation} | (15) |
$\textbf{Remark 1.}$ Udwadia and Kalaba have provided explicit general equations of motion for constrained discrete dynamical systems with their new initiated approach which is applicable to all holonomic and nonholonomic constrained systems no matter whether they satisfy the D'Alember's principle. They generalize Lagrangian mechanics to include both ideal and nonideal constraint forces by using a new fundamental principle governing the motion of constrained systems. The equation of motion obtained by using Udwadia and Kalaba's approach is general, simple and understandable.
$\textbf{Remark 2.}$ The advantage of determining the explicit equations of motion for this constrained coordinated robot system through Udwadia-Kalaba equation is obvious. Compared to the Lagrange multiplier method, there is no need for this new approach to determine the multiplier which is often very difficult to obtain for systems having a large number of degrees of freedom and many non-integrable constraints. Also, if using the formulations offered by Gibbs, Volterra, Appell and Boltzmann, we will require a proper quasi-coordinates, but we do not have this problem using the new initiated approach.
II. CONSTRAINT-FOLLOWING SERVO CONTROL APPROACH
According to Chen's constraint-following servo control approach, the system is now equipped with a set of servo controls which generate the active external forces to manipulate the behavior of the system. Suppose that the system is to follow a set of constraints which are determined by system performance requirements. The constraints are realized by servo controls instead of the passive environment. So, the equation of motion (6) of the system is now described as
| \begin{equation}\label{3.1} M\ddot q=Q+Q^c+Q^c_s, \end{equation} | (16) |
The constraint force is provided by the active servo controls. Based on the available controls, the structure of the constraint force is predetermined as
| \begin{equation}\label{3.2} Q^c_s=Bu, \end{equation} | (17) |
Consider the following constraints which the system is to follow:
| \begin{equation}\label{3.3} \sum_{i=1}^nA_{li}(q, t)\dot{q_i}+A_{l}(q, t)=0, \quad l=1, \ldots, m, \end{equation} | (18) |
Now the constraints are converted into second order form. Differentiating constraint equation (6) with respect to $t$ yields
| \begin{equation}\label{3.4} \sum_{i=1}^n\frac{{\rm d}}{{\rm d}t}A_{li}(q, t)\dot{q_i}+\sum_{i=1}^nA_{li}(q, t)\ddot{q_i}+\frac{{\rm d}}{{\rm d}t}A_{l}(q, t)=0, \end{equation} | (19) |
| \begin{equation}\label{3.5} \frac{{\rm d}}{{\rm d}t}A_{li}(q, t)=\sum_{i=1}^n\frac {\partial A_{li}(q, t)}{\partial q_k}\dot q_k+\frac {\partial A_{li}(q, t)}{\partial t}, \end{equation} | (20) |
| \begin{equation}\label{3.6} \frac{{\rm d}}{{\rm d}t}A_{l}(q, t)=\sum_{i=1}^n\frac {\partial A_{l}(q, t)}{\partial q_k}\dot q_k+\frac {\partial A_{l}(q, t)}{\partial t}, \end{equation} | (21) |
| \begin{align}\label{3.7} &\sum_{i=1}^nA_{li}(q, t)\ddot{q_i}=-\sum_{i=1}^n\frac{{\rm d}}{{\rm d}t}A_{li}(q, t)\dot{q_i}-\frac{{\rm d}}{{\rm d}t}A_{l}(q, t)\notag\\ &\quad=:b_i(\dot q, q, t), ~~l=1, \ldots, m, \end{align} | (22) |
| \begin{equation}\label{3.8} A(q, t)\ddot q=b(\dot q, q, t), \end{equation} | (23) |
In fact, the second order form constraint equation (23) is a very general form. It includes typical constraints as illustrated in [22, 23]. It also includes a number of standard control problems such as stabilization, trajectory following and optimality[20, 21].
The servo constraint problem can now be stated as follows: Determine the servo control $u$ such that when constraint force $Q^c_s$ is applied to system equation (6), the resulting controlled system observes constraint (23).
We see that, in general, there is no relationship between $B$ and $A$. $B$ is determined by the available servo controls and $A$ is based on the performance requirement. Actually, in the passive constraint problem, one can still use (16) and (23) by introducing $B = A$. The constraint force is generated by the environment not the servo control. Thus, passive constraint problem is reduced to a special case.
$\textbf{Assumption 1.}$ For each $q$, $M(q) > 0$.
The assumption of the inertia matrix's positive definiteness is vital for this constraint-following servo approach. In the past, this assumption was often believed to be a fact. However, this belief has been shown to be untrue in Chen et al.[24].
$\textbf{Definition 1.}$ For given $A$ and $b$, the constraint equation (23) is said to be consistent if there exists at least one solution $\ddot q$.
The consistency is a necessary but not a sufficient condition to the servo constraint problem. That is, if the constraint equation (23) is not consistent, then there is no solution $u$ to the servo constraint problem.
$\textbf{Assumption 2.}$ Considering constraint equation (23), for each $q$, $t$, rank $A(q, t)\geq1$. Also, the constraint is consistent. (This assumption ensures the existence of the Moore- Penrose inverse of $A$.)
Let
| \begin{equation}\label{3.9} \ddot x=M^{\frac{1}{2}}\ddot q, \quad a:=M^{-\frac{1}{2}}(Q+Q^c), \quad F^c_s=M^{-\frac{1}{2}}Q^c_s. \end{equation} | (24) |
System equation (16) can be represented as
| \begin{equation}\label{3.10} \ddot x=a+F^c_s=a+M^{-\frac{1}{2}}Q^c_s=a+\bar{B}u, \end{equation} | (25) |
| \begin{equation}\label{3.11} C\ddot x=b, \end{equation} | (26) |
$\textbf{Lemma 1.}$ Subject to Assumption 2, (23) is consistent if and only if
| \begin{equation}\label{3.12} AA^+b=b. \end{equation} | (27) |
$\textbf{Lemma 2.}$ Subject to Assumption 1, "for given $A$ and $b$, (23) is consistent" is equivalent to "for given $C$ and $b$, (26) is consistent".
$\textbf{Lemma 3.}$ Subject to Assumptions 1 and 2, the solution of (26) can be given by (see proof in [17])
| \begin{equation}\label{3.13} \ddot x=C^+b+(I-C^+C)c, \end{equation} | (28) |
$\textbf{Lemma 4.}$ Subject to Assumptions 1 and 2, the constraint force $F^c_s$ is given by (see proof in [17])
| \begin{equation}\label{3.14} F^c_s=C^+(b-Ca)+(I-C^+C)c, \end{equation} | (29) |
Because $r$ is arbitrary, we have
| \begin{equation}\label{3.15} \min_{r}\left\|F_s^c\right\|=C^+(b-Ca), \end{equation} | (30) |
Reference [8] considered a passive constraint problem and the constraint force is given by
| \begin{equation}\label{3.16} \ddot x=a+C^+(b-Ca), \end{equation} | (31) |
Now we focus on the design of $u$.
$\textbf{Definition 2.}$ The system equation (25) is said to be servo constraint controllable if there is a control $u$ such that the system under this control observes the constraint equation (26).
Let $\bar{b}:=b-Ca$. For given $C, \bar{B}, \bar{b}$, consider the equation
| \begin{equation}\label{3.17} (C\bar{B})u=\bar{b}. \end{equation} | (32) |
$\textbf{Assumption 3.}$ Considering $C, \bar{B}, \bar{b}$, (32) is consistent and hence
| \begin{equation}\label{3.18} (C\bar{B})(C\bar{B})^+\bar{b}=\bar{b}. \end{equation} | (33) |
$\textbf{Theorem 1.}$ Subject to Assumptions 1-3, the system equation (25) is servo constraint controllable if and only if
| \begin{equation}\label{3.19} {\rm rank}[C\bar{B}]\geq 1. \end{equation} | (34) |
| \begin{equation}\label{3.20} u=(C\bar{B})^+\bar{b}+[I-(C\bar{B})^+(C\bar{B})]s, \end{equation} | (35) |
We summarize the constraint-following servo control procedure as follows.
1) Based on Udwadia-Kalaba approach, impose the additional generalized constraint forces $Q^c$ obtained from the second order constraint equations upon the unconstrained system to obtain Udwadia-Kalaba equation.
2) Determine the servo structure by choosing $B$ to get $Q_s^c$ in (17). Then, the dynamic system is formulated in the form of (16).
3) Determine the desirable system performance in the task space and formulate it in the form of (23).
4) Obtain $C, \bar{B}, \bar{b}$ by $C=AM^{-\frac{1}{2}}, ~\bar{B}=M^{-\frac{1}{2}}B, ~\bar{b}=b-Ca, ~ a=M^{-\frac{1}{2}}(Q+Q^c)$.
5) Construct the feedback control $u$ using (35).
III. DISCUSSIONS ON THE PROPOSED SYSTEMATIC APPROACH
The proposed approach is novel and systematic because it uses constraint-following servo control based on the dynamic model obtained through Udwadia-Kalaba approach. In this section, we give more discussions.
A. Inverse Dynamics Based on Moore-Penrose Generalized Inverse
The concept of generalized inverse was first introduced by Moore[18]. He defined a unique inverse for all rectangular and square matrices and systematically investigated properties of this inverse. Bjerhammar[26] then noted the least squares property which was not mentioned by Penrose[19] sharpened and extended Bjerhammer's work. Due to Moore and Penrose's important and fruitful discovery, this unique inverse is commonly called Moore-Penrose generalized inverse (MP inverse).
More recently, MP inverse, which plays a role in least-squares problem, has found renewed applicability in the field of analytical dynamics[7]. Based on MP inverse, Udwadia-Kalaba equation[9] is derived. MP inverse also finds its advantage in the inverse dynamics control problem. The inverse dynamics control problem is to determine the control inputs that force the system to realize the specified motion. MP inverse overcomes the limitation of dimensionality and rank that are related to matrix's inversion. The proposed novel approach incorporates Udwadia-Kalaba approach and constraint-following servo control (one method of inverse dynamics control) that are both based on MP inverse. Thus, the proposed approach is expected to solve underactuated and redundantly actuated (also called overactuated) problems. This will be detailed in the following section.
B. Second-order Constraints and Constraint Drift Suppression
The constraint used in Lagrangian's equation of motion, Maggi equation, Boltzmann and Hamel equation as well as Gibbs and Appell equation is either in the zeroth- or first-order form. While, the constraint (holonomic or nonholonomic) of Udwadia-Kalaba equation is first converted into a second-order form, which is a critical step. Due to the mathematical conformity between the system dynamics and constraint, it is much more flexible to manipulate the equations. Second-order constraints are believed to be the most suitable form, not only for further dynamic analysis but also control design. In the constraint-following servo control design, the constraint is also in the form of second order.
Historically, the second-order constraint has been rarely mentioned perhaps because of the lack of physical correspondence. Pars[5] utilized this aspect to explore a number of interesting applications. By adopting the third form of fundamental equation (constraints of large acceleration changes), one can analyze discontinuous acceleration problems (e.g., a ball rolling off the table). This third form was also used to prove the Gauss's principle. With second-order constraint, Udwadia-Kalaba equation and constraint-following servo control were able to be developed. The advantage of using the second-order constraint lies in the fact that it is linear in the acceleration.
One may think that the differentiation of the constraint has resulted in the loss of information (e.g., a constant). However, the initial condition of the state satisfies the zeroth-order or holonomic constraint which means the missing information is, in fact, retained in the initial condition.
The solution of differential equations of second-order constraints satisfies an analytical relation which is a corollary of the differential equations but which is unknown to the automatic computer. When differential equations are integrated by numerical and automatic integration, the computed numerical values of the solution satisfy the analytic relations with poor accuracy. This is called constraint drift. Direct numerical integration of the second-order constraint generally leads to error accumulation due to constraint drift.
In order to enable stable numerical simulation without error accumulation and ensure that the small numerical error made at each integration step does not accumulate along the solution process, Baumgarte's constraint stabilization is used[27]. This constraint violation suppression method is one of the most popular methods in engineering practice and does not require iterative constraint corrections. We use this method to conduct the numerical simulation. Instead of using the original second-order constraint, $\phi=A\ddot q-b=0$, we use a corresponding equation, $\ddot \phi+2\alpha\dot \phi+\beta^2\phi=0, ~\alpha=\beta>0$ which has a globally asymptotically stable solution approaching zero ($\phi=0$) over time.
C. Underactuated and Redundantly Actuated Problems
Underactuated problem is actually partly specified motion problem, in which the number of control inputs, equal to the number of desired system outputs, is smaller than the number of degrees of freedom. The related inverse dynamics control problem, i.e., the determination of control inputs that force the system to complete the partly specified motion, is a challenging task. Examples of underactuated systems are mobile robots, legged robots, space robots, flexible robots and so on. The difficulty of the control problem for underactuated systems is due to the reduced dimension of the input space (some joints are not equipped with actuators). When the number of actuators is greater than the mobility (this situation usually happens in a closed-chain system), the system is called redundantly actuated system. Redundant actuation prevails in general biomechanical systems (e.g., human body). It can also be found in many robotic applications including multiple arms, multi-fingered arms, walking machines and so on. Redundant actuation provides flexible manipulation, high reliability, high driving force and so on, while the principle drawback is the complexity of singularity analysis. However, this proposed approach is expected to solve underactuated and redundantly actuated problems mainly because of MP inverse (overcoming the limitation of dimensionality) and second-order constraints (mathematical conformity).
IV. TWO-MASS SPRING SYSTEM
A simple representative of underactuated problems is the two-mass spring system shown in Fig. 1, in which the actuating force $F$ is applied to mass $m_1$, and the motion specification is a desired relation between position $x_1$ of mass $m_1$ and position $x_2$ of mass $m_2$. This is a two-degree-of-freedom system, $n=2$, and the number of control inputs/outputs is $m=1$. First, note that,
| \begin{eqnarray}\label{5.1} T=\frac{1}{2}m_1\dot x_1^2+\frac{1}{2}m_2\dot x_2^2, ~V=\frac{1}{2}k(x_2-x_1-l)^2, \end{eqnarray} | (36) |
| \[\frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial {{\dot x}_1}}} - \frac{{\partial L}}{{\partial {x_1}}} = {m_1}{\ddot x_1} - k({x_2} - {x_1} - l) = F, \] | (37) |
| \[\frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial {{\dot x}_2}}} - \frac{{\partial L}}{{\partial {x_2}}} = {m_2}{\ddot x_2} + k({x_2} - {x_1} - l) = 0.\] | (38) |
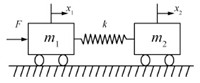 | Download: |
| Fig. 1 Two-mass spring system. | |
The system can be put into the form of (16) by letting
| \[q{\rm{ = }}\left[{\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right], M = \left[{\begin{array}{*{20}{c}} {{m_1}}&0\\ 0&{{x_2}} \end{array}} \right], \] | (39) |
| \[{Q^c} = \left[{\begin{array}{*{20}{c}} {k({x_2} - {x_1} - l)}\\ { - k({x_2} - {x_1} - l)} \end{array}} \right], \] | (40) |
| \[Q = \left[{\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right], Q_s^c = \left[{\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right]F.\] | (41) |
Furthermore, we can convert it into the form of (25) with
| \[\ddot x = \left[{\begin{array}{*{20}{c}} {m_1^{\frac{1}{2}}{{\ddot x}_1}}\\ {m_2^{\frac{1}{2}}{{\ddot x}_2}} \end{array}} \right], \bar B = \left[{\begin{array}{*{20}{c}} {m_1^{ - \frac{1}{2}}}\\ 0 \end{array}} \right], \] | (42) |
| \[a = \left[{\begin{array}{*{20}{c}} {m_1^{ - \frac{1}{2}}k({x_2} - {x_1} - l)}\\ { - m_2^{ - \frac{1}{2}}k({x_2} - {x_1} - l)} \end{array}} \right].\] | (43) |
The servo constraint to be realized is
| \begin{eqnarray} x_2-x_1=2l, \end{eqnarray} | (44) |
| \begin{eqnarray} \underbrace{\left[\begin{array}{cc} -1&1 \end{array} \right]}_{A} \underbrace{\left[\begin{array}{c} \ddot x_1\\ \ddot x_2 \end{array} \right]}_{\ddot q}=\underbrace{0}_{b} \end{eqnarray} | (45) |
| \begin{eqnarray} \underbrace{\left[\begin{array}{cc} -m_1^{-\frac{1}{2}}&m_2^{-\frac{1}{2}} \end{array} \right]}_{C} \underbrace{\left[\begin{array}{c} m_1^{\frac{1}{2}}\ddot x_1\\ m_2^{\frac{1}{2}}\ddot x_2 \end{array} \right]}_{\ddot x}=\underbrace{0}_{b}. \end{eqnarray} | (46) |
For the design of control $F$, since $C\bar{B}=-m_1^{-1}\neq 0$, we note that the system is servo constraint controllable. The control is thus given by
| \begin{align} F&=(C\bar{B})^+\bar{b}+[1-(C\bar{B})^+(C\bar{B})]S=(C\bar{B})^+\bar{b}+0\notag\\ &=-(1+m_1m_2^{-1})k(x_2-x_1-l). \end{align} | (47) |
V. COORDINATED ROBOT SYSTEM
In this system, two coordinated robots (each robot has $s$ links) handle the common load. Because the common load or object is rigidly held by the two end effectors (i.e., fixed together, no sliding or rotation), the two end effectors and the common object are considered as one link. The whole system is considered as a closed chain. According to Udwadia and Kalaba's approach, first we should obtain the equations of motion of the unconstrained dynamical system (serial manipulators of $n=2s-1$ links). Then, get the constraint (the end link hinged to the ground) and rewrite the constraint equations in the form of second-order. In the end, impose the additional generalized constraint forces obtained from the second-order constraint equations upon the unconstrained system to get Udwadia-Kalaba equation which is in analytical form.
As we know, the closed-form dynamic equations of any serial manipulators $n$ links can be obtained through the systematical Lagrangian formulation. The dynamics is strongly nonlinear and can be written in the general form
| \begin{equation}\label{6.1} M(q) \ddot q+C(q, \dot q)\dot q+G(q)=\tau, \end{equation} | (48) |
According to the systematical derivation of [28](pp. 104-110), we get
| \begin{equation}\label{6.2} M(q)=\sum_{i=1}^{n}\left(m_iJ_L^{(i){\rm T}}J_L^{(i)}+J_A^{(i){\rm T}}I_iJ_A^{(i)}\right), \end{equation} | (49) |
| \begin{eqnarray}\label{6.3} v_{ci}=J_{L1}^{(i)}\dot q_1+\cdots+J_{Li}^{(i)}\dot q_i=J_{L}^{(i)}\dot q, \nonumber\\ \omega_i=J_{A1}^{(i)}\dot q_1+\cdots+J_{Ai}^{(i)}\dot q_i=J_{A}^{(i)}\dot q, \end{eqnarray} | (50) |
| \begin{eqnarray}\label{6.4} J_{L}^{(i)}=[J_{L1}^{(i)} \ldots J_{Li}^{(i)} 0 \ldots 0], \nonumber\\ J_{A}^{(i)}=[J_{A1}^{(i)} \ldots J_{Ai}^{(i)} 0 \ldots 0]. \end{eqnarray} | (51) |
For the $n$-link manipulators, the Coriolis and centripetal torque vector $C\dot q$ can be uniquely defined. But this does not define the matrix $C$ uniquely. However, according to [29], a particular choice of the matrix $C$ which guarantees the matrix $\dot M-2C$ to be skew-symmetric is given by
| \begin{equation}\label{6.5} c_{ij}=\frac{1}{2}\sum_{k=1}^{n}\frac{\partial m_{ij}}{\partial q_k}\dot q_k+\frac{1}{2}\sum_{k=1}^{n}\left(\frac{\partial m_{ik}}{\partial q_j}-\frac{\partial m_{jk}}{\partial q_i}\right)\dot q_k, \end{equation} | (52) |
According to the systematical derivation of [28](pp. 104-110), we also get
| \begin{equation}\label{6.6} G_i=\sum_{j=1}^n m_j{\pmb g}^{\rm T}J_{Li}^{(j)}, \end{equation} | (53) |
The closed-form dynamic equations of the $n$-link serial manipulators is obtained. This is considered as the equation of motion of the unconstrained dynamical system. Then, we consider the second order constraint equation and constraint force. The end link hinged to the ground is considered as the constraint. So we get can get the holonomic constraints. Taking time derivation twice on the holonomic constraints, we can get second order constraint equations which can be written in the matrix form
| \begin{equation}\label{6.7} \hat{A}(q, \dot q, t)\ddot q = \hat{b}(q, \dot q, t). \end{equation} | (54) |
According to (14), we can get the constraint force $Q^c$.
Then, we impose the additional generalized constraint force $Q^c$ obtained from the second-order constraint equations upon the unconstrained system to get Udwadia-Kalaba equation which is in analytical form. We can rewrite (48) as
| \begin{equation}\label{6.8} M(q) \ddot q=Q, \end{equation} | (55) |
| \begin{equation}\label{6.9} M(q) \ddot q=Q+Q^c. \end{equation} | (56) |
${\bf Remark 3.}$ In (56), $M, Q, Q^c$ have already been obtained. It provides explicit general equations of motion for the closed chain of two coordinated robots. We have shown the equation of motion obtained by using Udwadia and Kalaba's approach is simple and understandable. We take two coordinated planar robot manipulators (each robot has $s=3$ links) to detail the approach. In this problem, $s=3, ~n=2s-1=5$ and $q=[\theta_1 ~\theta_2 ~\theta_3 ~\theta_4 ~\theta_5]^{\rm T}$. Fig. 2 clearly shows the structure of the whole robot system. The two coordinated robots have $6$ joints and every joint has one actuator. However, we can obtain the system dynamic equation (16) using $5$ generalized coordinates ($\theta_1, \theta_2, \theta_3, \theta_4, \theta_5$) and the degree of freedom of the coordinated robot system is $3$. That is to say, servo control of the coordinated robot is actually a redundantly actuated problem. We will show that the proposed approach applies to this redundantly actuated problem.
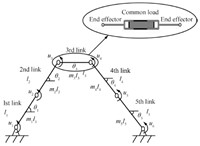 | Download: |
| Fig. 2 Model of two coordinated planar robot manipulators handling the common load. | |
First, we do not consider the constraint of the end link hinged to the ground. For this unconstrained dynamical system (the five-link manipulator), we know
| \begin{eqnarray}\label{6.10} &x_1=\frac{l_1}{2}\cos\theta_1, ~~~~&y_1=\frac{l_1}{2}\sin\theta_1, \nonumber \\ &\dot x_1=-\frac{l_1}{2}\sin\theta_1\dot \theta_1, &\dot y_1=\frac{l_1}{2}\cos\theta_1\dot \theta_1, \end{eqnarray} | (57) |
| \[{v_{c1}} = \left[{\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\dot y}_1}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\frac{{{l_1}}}{2}\sin {\theta _1}}&0&0&0&0\\ {\frac{{{l_1}}}{2}\cos {\theta _1}}&0&0&0&0 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\dot \theta }_1}}\\ {{{\dot \theta }_2}}\\ {{{\dot \theta }_3}}\\ {{{\dot \theta }_4}}\\ {{{\dot \theta }_5}} \end{array}} \right], \] | (58) |
| \[\begin{array}{*{20}{c}} {{\omega _1} = {{\dot \theta }_1} = \left[{\begin{array}{*{20}{c}} 1&0&0&0&0 \end{array}} \right]q, }\\ {{\omega _2} = {{\dot \theta }_2} = \left[{\begin{array}{*{20}{c}} 0&1&0&0&0 \end{array}} \right]q, }\\ {{\omega _3} = {{\dot \theta }_3} = \left[{\begin{array}{*{20}{c}} 0&0&1&0&0 \end{array}} \right]q, }\\ {{\omega _4} = {{\dot \theta }_4} = \left[{\begin{array}{*{20}{c}} 0&0&0&1&0 \end{array}} \right]q, }\\ {{\omega _5} = {{\dot \theta }_5} = \left[{\begin{array}{*{20}{c}} 0&0&0&0&1 \end{array}} \right]q, } \end{array}\] | (59) |
According to (49)-(51), we get the matrix $M$ (shown in Appendix). According to (52), we get the matrix $C$ (shown in Appendix). According to (53), we know ${\pmb g}=[0 ~g]^{\rm T}$ and get the matrix $G$ (shown in Appendix). The impressed force $\tau$ is ${0}$. So, equations of motion (48) of $5$-link serial manipulators (unconstrained dynamic system) is obtained through the systematical Lagrangian formulation.
Considering the constraint of the end link hinged to the ground, we get
| \[\begin{array}{*{20}{l}} {{l_1}\cos {\theta _1} + {l_2}\cos {\theta _2} + {l_3}\cos {\theta _3} + {l_4}\cos {\theta _4} + {l_5}\cos {\theta _5} = L, }\\ {{l_1}\sin {\theta _1} + {l_2}\sin {\theta _2} + {l_3}\sin {\theta _3} + {l_4}\sin {\theta _4} + {l_5}\sin {\theta _5} = 0, } \end{array}\] | (60) |
| \[\begin{array}{*{20}{l}} { - {l_1}\sin {\theta _1}{{\ddot \theta }_1} - {l_2}\sin {\theta _2}{{\ddot \theta }_2} - {l_3}\sin {\theta _3}{{\ddot \theta }_3}}\\ {\quad - {l_4}\sin {\theta _4}{{\ddot \theta }_4} - {l_5}\sin {\theta _5}{{\ddot \theta }_5}}\\ {\quad = {l_1}\cos {\theta _1}\dot \theta _1^2 + {l_2}\cos {\theta _2}\dot \theta _2^2 + {l_3}\cos {\theta _3}\dot \theta _3^2}\\ {\quad + {l_4}\cos {\theta _4}\dot \theta _4^2 + {l_5}\cos {\theta _5}\dot \theta _5^2, }\\ {\quad {l_1}\cos {\theta _1}{{\ddot \theta }_1} + {l_2}\cos {\theta _2}{{\ddot \theta }_2} + {l_3}\cos {\theta _3}{{\ddot \theta }_3}}\\ {\quad + {l_4}\cos {\theta _4}{{\ddot \theta }_4} + {l_5}\cos {\theta _5}{{\ddot \theta }_5}}\\ {\quad = {l_1}\sin {\theta _1}\dot \theta _1^2 + {l_2}\sin {\theta _2}\dot \theta _2^2 + {l_3}\sin {\theta _3}\dot \theta _3^2}\\ {\quad + {l_4}\sin {\theta _4}\dot \theta _4^2 + {l_5}\sin {\theta _5}\dot \theta _5^2.} \end{array}\] | (61) |
The above second-order constraint equations can be written in the matrix form
| \[\hat A(q, \dot q, t)\ddot q = \hat b(q, \dot q, t), \] | (62) |
| \[\begin{array}{*{20}{l}} \begin{array}{l} \hat A = \\ \;\;\;\;\left[{\begin{array}{*{20}{c}} { - {l_1}\sin {\theta _1}}&{ - {l_2}\sin {\theta _2}}&{ - {l_3}\sin {\theta _3}}&{ - {l_4}\sin {\theta _4}}&{ - {l_5}\sin {\theta _5}}\\ {{l_1}\cos {\theta _1}}&{{l_2}\cos {\theta _2}}&{{l_3}\cos {\theta _3}}&{{l_4}\cos {\theta _4}}&{{l_5}\cos {\theta _5}} \end{array}} \right], \end{array}\\ {\hat b = \left[{\begin{array}{*{20}{c}} {{l_1}\cos {\theta _1}\dot \theta _1^2 + {l_2}\cos {\theta _2}\dot \theta _2^2 + {l_3}\cos {\theta _3}\dot \theta _3^2}\\ { + {l_4}\cos {\theta _4}\dot \theta _4^2 + {l_5}\cos {\theta _5}\dot \theta _5^2}\\ {{l_1}\sin {\theta _1}\dot \theta _1^2 + {l_2}\sin {\theta _2}\dot \theta _2^2 + {l_3}\sin {\theta _3}\dot \theta _3^2 + }\\ {{l_4}\sin {\theta _4}\dot \theta _4^2 + {l_5}\sin {\theta _5}\dot \theta _5^2} \end{array}} \right]} \end{array}\] | (63) |
According to (14), we can get the constraint force $Q^c$. We know $Q=\tau-C\dot q-G$. So, Udwadia-Kalaba equation (56) is obtained.
The two coordinated planar robots system is considered as a closed kinematic chain and the dynamic equation has already been obtained. Now we focus on the servo control of the system. We first describe the performance requirement of the object in the task space. For simulation, we choose
| \[\begin{array}{*{20}{c}} {{x_3} = 1.5l, {y_3} = \frac{l}{2}(1 - \cos (t)), {\theta _3} = 0, }\\ {{{\dot x}_3} = 0, {{\dot y}_3} = \frac{l}{2}\sin (t), {{\dot \theta }_3} = 0, }\\ {{{\ddot x}_3} = 0, {{\dot y}_3} = \frac{l}{2}\cos (t), {{\dot \theta }_3} = 0.} \end{array}\] | (64) |
This performance requirement is considered as constraints. We also know that
| \[\begin{array}{*{20}{c}} {{x_3} = {l_1}\cos {\theta _1} + {l_2}\cos {\theta _2} + \frac{{{l_3}}}{2}\cos {\theta _3}, }\\ {{y_3} = {l_1}\sin {\theta _1} + {l_2}\sin {\theta _2} + \frac{{{l_3}}}{2}\sin {\theta _3}.} \end{array}\] | (65) |
Differentiating the above equation once and twice, we get
| \[\begin{array}{*{20}{l}} {{{\dot x}_3} = - {l_1}\sin {\theta _1}{{\dot \theta }_1} - {l_2}\sin {\theta _2}{{\dot \theta }_2} - \frac{{{l_3}}}{2}\sin {\theta _3}{{\dot \theta }_3}, }\\ {{{\dot y}_3} = {l_1}\cos {\theta _1}{{\dot \theta }_1} + {l_2}\cos {\theta _2}{{\dot \theta }_2} + \frac{{{l_3}}}{2}\cos {\theta _3}{{\dot \theta }_3}, }\\ {{{\ddot x}_3} = - {l_1}\sin {\theta _1}{{\ddot \theta }_1} - {l_2}\sin {\theta _2}{{\ddot \theta }_2} - \frac{{{l_3}}}{2}\sin {\theta _3}{{\ddot \theta }_3}}\\ {\quad - {l_1}\cos {\theta _1}{{\dot \theta }_1}^2 - {l_2}\cos {\theta _2}{{\dot \theta }_2}^2 - \frac{{{l_3}}}{2}\cos {\theta _3}{{\dot \theta }_3}^2, }\\ {{{\ddot y}_3} = {l_1}\cos {\theta _1}{{\ddot \theta }_1} + {l_2}\cos {\theta _2}{{\ddot \theta }_2} + \frac{{{l_3}}}{2}\cos {\theta _3}{{\ddot \theta }_3}}\\ {\quad - {l_1}\sin {\theta _1}{{\dot \theta }_1}^2 - {l_2}\sin {\theta _2}{{\dot \theta }_2}^2 - \frac{{{l_3}}}{2}\sin {\theta _3}{{\dot \theta }_3}^2.} \end{array}\] | (66) |
These second order constraints can be represented in the form of matrix as (recalling (64))
| \[A\ddot q = b, \] | (67) |
| \[\begin{array}{l} A = \left[{\begin{array}{*{20}{c}} { - {l_1}\sin {\theta _1}}&{ - {l_2}\sin {\theta _2}}&{ - \frac{{{l_3}}}{2}\sin {\theta _3}}&0&0\\ {{l_1}\cos {\theta _1}}&{{l_2}\cos {\theta _2}}&{\frac{{{l_3}}}{2}\cos {\theta _3}}&0&0\\ 0&0&1&0&0 \end{array}} \right], \\ b = \left[{\begin{array}{*{20}{c}} {{l_1}\cos {\theta _1}\dot \theta _1^2 + {l_2}\cos {\theta _2}\dot \theta _2^2 + \frac{{{l_3}}}{2}\cos {\theta _3}\dot \theta _3^2}\\ {{l_1}\sin {\theta _1}\dot \theta _1^2 + {l_2}\sin {\theta _2}\dot \theta _2^2 + \frac{{{l_3}}}{2}\sin {\theta _3}\dot \theta _3^2 + \frac{l}{2}\cos (t)}\\ 0 \end{array}} \right]. \end{array}\] | (68) |
We should determine the servo structure by choosing $B$ in (17). Based on the available servo controls (see Fig. 2), we get
| \[Q_s^c = Bu, \] | (69) |
| \[B = \left[{\begin{array}{*{20}{c}} 1&{ - 1}&0&0&0&0\\ 0&1&{ - 1}&0&0&0\\ 0&0&1&1&0&0\\ 0&0&0&{ - 1}&1&0\\ 0&0&0&0&{ - 1}&1 \end{array}} \right], \] | (70) |
VI. NUMERICAL SIMULATION
Control of this two coordinated planar robots system is a redundantly actuated control. According to (35), we know the solution of control $u$ is not unique. For simulation, we take
| \[u = (C\overline B ) + \overline b , \] | (71) |
For simulation, we choose $m_1=m_2=m_3=m_4=m_5=1, I_1=I_2=I_3=I_4=I_5=1, l_1=l_2=l_3=l_4=l_5=l=1, g=9.8$. The initial configuration of the system is presented in Fig. 3. The initial position, velocity and acceleration are shown in Table I. The second-order constraint equation does not result in the loss of of information. Because the initial condition satisfies the zeroth-order (holonomic) and first-order constraint. The missing information is retained in the initial condition.
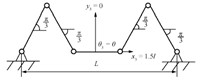 | Download: |
| Fig. 3 The initial configuration of the system. | |
| Table I INITIAL CONDITION OF THE COORDINATED ROBOT SYSTEM |
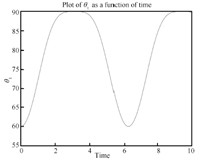
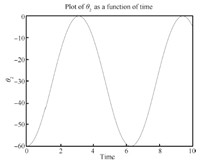
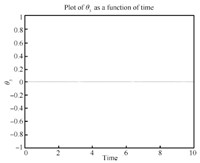
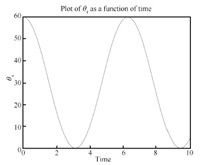
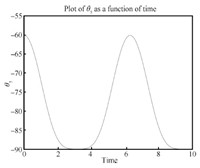
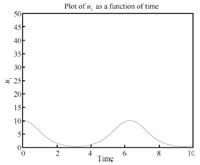
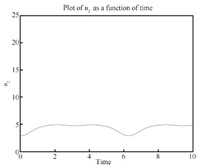
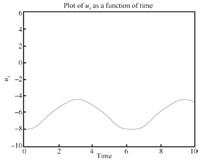
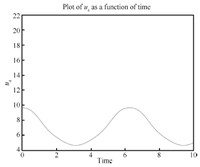
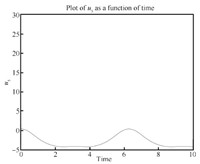
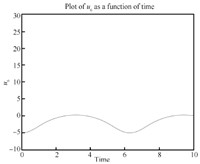
We can see the simulation results in Figs. 4- 14. From Fig. 6, we know $\theta_3, \dot \theta_3, \ddot \theta$ are all zero, which means the third link always remains horizontal. and Fig. 8 show that the first and fifth link move from the initial configuration to the upwardly vertical position (where the object is in the highest vertical position $y_3=l=1$) and then come back to the initial position. Figs. 5 and 7 show that the second and fourth link move from the initial configuration to the horizontal position (where the object is in the highest vertical position) and then come back to the initial position. So link 1, 2, 4, 5's movements are periodic which leads to the periodic moving of the object (the third link) from $y_3=0$ (the lowest position) to $y_3=l=1$ (the highest position) and then back to the lowest position. So the desirable performance ($x_3$ is always $1.5l$, $y_3=\frac{l}{2}(1-\cos(t))$, $\theta_3$ is always zero) is realized by the servo controls which can be seen in Figs. 9-14. For the actuators of the first robot, in Figs. 9, $u_1$ fluctuates from $0$ to $10$. Fig. 10 shows that $u_2$'s magnitude is from about $3$ to $5$. From Fig. 11, we see $u_3$ runs from minimum $-8$ to maximum $-5.5$. For the other robot, Fig. 12 shows $u_4$'s amplitude is from about $4.5$ to $10$ while amplitude of $u_5$ in Fig. 13 is from $-4.5$ to $0.5$ and $u_6$ in Fig. 14 shows its magnitude runs from minimum $-5$ to maximum $0$.
 | Download: |
| Fig. 4 $\theta_1-t$. | |
 | Download: |
| Fig. 5 $\theta_2-t$. | |
 | Download: |
| Fig. 6 $\theta_3-t$. | |
 | Download: |
| Fig. 7 $\theta_4-t$. | |
 | Download: |
| Fig. 8 $\theta_5-t$. | |
 | Download: |
| Fig. 9 $u_1-t$. | |
 | Download: |
| Fig. 10 $u_2-t$. | |
 | Download: |
| Fig. 11 $u_3-t$. | |
 | Download: |
| Fig. 12 $u_4-t$. | |
 | Download: |
| Fig. 13 $u_5-t$. | |
 | Download: |
| Fig. 14 $u_6-t$. | |
VII. CONCLUSION
We propose a novel and systematic approach for dynamic modeling and servo control of constrained mechanical systems. In this approach, Udwadia-Kalaba equation is applied to obtain the additional generalized constraint force and then get the system's dynamic equation. Second-order constraint equations are used, which do not result in the loss of information because of the initial condition satisfying the zeroth-order (holonomic) and first-order constraint. For the control part, we propose to adopt the constraint-following servo control design approach which can solve fully actuated, underactuated and redundantly actuated systems. According to this control design approach, we first represent the desirable performance as a set of second order equations. Then we consider the performance requirement as the constraint and use a set of servo controls to generate appropriate constraint forces for the system to obey the constraints. Detailed discussions of the proposed approach are presented. Two-mass spring system and coordinated robots system are presented as examples for illustration.
APPENDIX
| \[\begin{array}{l} J_{L1}^{(2)} = J_{L1}^{(3)} = J_{L1}^{(4)} = J_{L1}^{(5)} = \left[{\begin{array}{*{20}{c}} { - {l_1}\sin {\theta _1}}\\ {{l_1}\cos {\theta _1}} \end{array}} \right], \\ J_{L2}^{(2)} = \left[{\begin{array}{*{20}{c}} { - \frac{{{l_2}}}{2}\sin {\theta _2}}\\ {\frac{{{l_2}}}{2}\cos {\theta _2}} \end{array}} \right], \\ J_{L2}^{(3)} = J_{L2}^{(4)} = J_{L2}^{(5)} = \left[{\begin{array}{*{20}{c}} { - {l_2}\sin {\theta _2}}\\ {{l_2}\cos {\theta _2}} \end{array}} \right], \\ J_{L3}^{(3)} = \left[{\begin{array}{*{20}{c}} { - \frac{{{l_3}}}{2}\sin {\theta _3}}\\ {\frac{{{l_3}}}{2}\cos {\theta _3}} \end{array}} \right], \\ J_{L3}^{(4)} = J_{L3}^{(5)} = J_{L2}^{(5)} = \left[{\begin{array}{*{20}{c}} { - {l_3}\sin {\theta _3}}\\ {{l_3}\cos {\theta _3}} \end{array}} \right], \\ J_{L4}^{(4)} = \left[{\begin{array}{*{20}{c}} { - \frac{{{l_4}}}{2}\sin {\theta _4}}\\ {\frac{{{l_4}}}{2}\cos {\theta _4}} \end{array}} \right], \\ J_{L4}^{(5)} = \left[{\begin{array}{*{20}{c}} { - {l_4}\sin {\theta _4}}\\ {{l_4}\cos {\theta _4}} \end{array}} \right], \\ J_{L5}^{(5)} = \left[{\begin{array}{*{20}{c}} { - \frac{{{l_5}}}{2}\sin {\theta _5}}\\ {\frac{{{l_5}}}{2}\cos {\theta _5}} \end{array}} \right]. \end{array}\] | (A1) |
| \[\begin{array}{*{20}{l}} {{M_{11}} = \left( {\frac{{{m_1}}}{4} + {m_2} + {m_3} + {m_4} + {m_5}} \right){l_1}^2 + {I_1}, }\\ {{M_{{\rm{12}}}}{\rm{ = }}{M_{21}} = \left( {\frac{{{m_2}}}{2} + {m_3} + {m_4} + {m_5}} \right){l_1}{l_2}\cos ({\theta _1} - {\theta _2}), }\\ {{M_{13}} = {M_{31}} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right){l_1}{l_3}\cos ({\theta _1} - {\theta _3}), }\\ {{M_{14}} = {M_{41}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_1}{l_4}\cos ({\theta _1} - {\theta _4}), }\\ {{M_{15}} = {M_{51}} = \frac{{{m_5}}}{2}{l_1}{l_5}\cos ({\theta _1} - {\theta _5}), }\\ {{M_{22}} = \left( {\frac{{{m_2}}}{4} + {m_3} + {m_4} + {m_5}} \right){l_2}^2 + {I_2}, }\\ {{M_{23}} = {M_{32}} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right){l_2}{l_3}\cos ({\theta _2} - {\theta _3}), }\\ {{M_{24}} = {M_{42}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_2}{l_4}\cos ({\theta _2} - {\theta _4}), }\\ {{M_{25}} = {M_{52}} = \frac{{{m_5}}}{2}{l_2}{l_5}\cos ({\theta _2} - {\theta _5}), }\\ {{M_{33}} = \left( {\frac{{{m_3}}}{4} + {m_4} + {m_5}} \right){l_3}^2 + {I_3}, }\\ {{M_{34}} = {M_{43}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_3}{l_4}\cos ({\theta _3} - {\theta _4}), }\\ {{M_{35}} = {M_{53}} = \frac{{{m_5}}}{2}{l_3}{l_5}\cos ({\theta _3} - {\theta _5}), }\\ {{M_{44}} = \left( {\frac{{{m_4}}}{4} + {m_5}} \right){l_4}^2 + {I_4}, }\\ {{M_{45}} = {M_{54}} = \frac{{{m_5}}}{2}{l_4}{l_5}\cos ({\theta _4} - {\theta _5}), }\\ {{M_{55}} = \frac{{{m_5}}}{4}{l_5}^2 + {I_5}.} \end{array}\] | (A2) |
| \[\begin{array}{*{20}{l}} {{C_{12}} = \left( {\frac{{{m_2}}}{2} + {m_3} + {m_4} + {m_5}} \right){l_1}{l_2}\sin ({\theta _1} - {\theta _2}){{\dot \theta }_2}, }\\ {{C_{13}} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right){l_1}{l_3}\sin ({\theta _1} - {\theta _3}){{\dot \theta }_3}, }\\ {{C_{14}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_1}{l_4}\sin ({\theta _1} - {\theta _4}){{\dot \theta }_4}, }\\ {{C_{15}} = \frac{{{m_5}}}{2}{l_1}{l_5}\sin ({\theta _1} - {\theta _5}){{\dot \theta }_5}, }\\ {{C_{21}} = \left( {\frac{{{m_2}}}{2} + {m_3} + {m_4} + {m_5}} \right){l_1}{l_2}\sin ({\theta _2} - {\theta _1}){{\dot \theta }_1}, }\\ {{C_{23}} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right){l_2}{l_3}\sin ({\theta _2} - {\theta _3}){{\dot \theta }_3}, }\\ {{C_{24}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_2}{l_4}\sin ({\theta _2} - {\theta _4}){{\dot \theta }_4}, }\\ {{C_{25}} = \frac{{{m_5}}}{2}{l_2}{l_5}\sin ({\theta _2} - {\theta _5}){{\dot \theta }_5}, }\\ {{C_{31}} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right){l_1}{l_3}\sin ({\theta _3} - {\theta _1}){{\dot \theta }_1}, }\\ {{C_{32}} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right){l_2}{l_3}\sin ({\theta _3} - {\theta _2}){{\dot \theta }_2}, }\\ {{C_{34}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_3}{l_4}\sin ({\theta _3} - {\theta _4}){{\dot \theta }_4}, }\\ {{C_{35}} = \frac{{{m_5}}}{2}{l_3}{l_5}\sin ({\theta _3} - {\theta _5}){{\dot \theta }_5}, }\\ {{C_{41}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_1}{l_4}\sin ({\theta _4} - {\theta _1}){{\dot \theta }_1}, }\\ {{C_{42}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_2}{l_4}\sin ({\theta _4} - {\theta _2}){{\dot \theta }_2}, }\\ {{C_{43}} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right){l_3}{l_4}\sin ({\theta _4} - {\theta _3}){{\dot \theta }_3}, }\\ {{C_{45}} = \frac{{{m_5}}}{2}{l_4}{l_5}\sin ({\theta _4} - {\theta _5}){{\dot \theta }_5}, }\\ {{C_{51}} = \frac{{{m_5}}}{2}{l_1}{l_5}\sin ({\theta _5} - {\theta _1}){{\dot \theta }_1}, }\\ {{C_{52}} = \frac{{{m_5}}}{2}{l_2}{l_5}\sin ({\theta _5} - {\theta _2}){{\dot \theta }_2}, }\\ {{C_{53}} = \frac{{{m_5}}}{2}{l_3}{l_5}\sin ({\theta _5} - {\theta _3}){{\dot \theta }_3}, }\\ {{C_{54}} = \frac{{{m_5}}}{2}{l_4}{l_5}\sin ({\theta _5} - {\theta _4}){{\dot \theta }_4}, }\\ {{\rm{C\_\{ 11\} = C\_\{ 22\} = C\_\{ 33\} = C\_\{ 44\} = C\_\{ 55\} = 0}}{\rm{.}}} \end{array}\] | (A3) |
| \[\begin{array}{l} {G_1} = \left( {\frac{{{m_1}}}{2} + {m_2} + {m_3} + {m_4} + {m_5}} \right)g{l_1}\cos {\theta _1}, \\ {G_2} = \left( {\frac{{{m_2}}}{2} + {m_3} + {m_4} + {m_5}} \right)g{l_2}\cos {\theta _2}, \\ {G_3} = \left( {\frac{{{m_3}}}{2} + {m_4} + {m_5}} \right)g{l_3}\cos {\theta _3}, \\ {G_4} = \left( {\frac{{{m_4}}}{2} + {m_5}} \right)g{l_4}\cos {\theta _4}, \\ {G_5} = \frac{{{m_5}}}{2}g{l_5}\cos {\theta _5}. \end{array}\] | (A4) |
| [1] | Lagrange J L. Mechanique Analytique. Paris: Mme ve Courcier, 1787. |
| [2] | Gauss C F. Uber ein neues allgemeines grundgsetz der mechanik. Journal fur die Reine und Angewandte Mathematik, 1829, 4: 232-235 |
| [3] | Gibbs J W. On the fundamental formulae of dynamics. American Journal of Mathematics, 1879, 2(1): 49-64 |
| [4] | Appell P. Sur une forme generale des equations de la dynamique. Comptes Rendus de l'Academie des Sciences, 1899, 129: 459-460 |
| [5] | Pars L A. A Treatise on Analytical Dynamics. Connecticut: Ox Bow Press, 1979. |
| [6] | Dirac P A M. Lectures on Quantum Mechanics. New York: Yeshiva University Press, 1964. |
| [7] | Udwadia F E, Kalaba R E. A new perspective on constrained motion. Proceedings of the Royal Society, 1992, 439(1906), doi: 10.1098/rspa.1992.0158 |
| [8] | Udwadia F E, Kalaba R E. Analytical Dynamics: A New Approach. Cambridge, UK: Cambridge University Press, 1996. |
| [9] | Udwadia F E, Kalaba R E. Explicit equations of motion for mechanical systems with nonideal constraints. Journal of Applied Mechanics, 2001, 68(3): 462-467 |
| [10] | Udwadia F E. On constrained motion. Applied Mathematics and Computation, 2005, 164(2): 313-320 |
| [11] | Maggi G A. Di alcune nuove forme delle equazioni della dinamica, applicabili ai sistemi anolonomi. Atti della Reale Accademia dei Lincei, Rendiconti, Classe di Scienze Fisiche, Matematiche e Naturali, 1901, 10: 287-291 (in Italian) |
| [12] | Neimark J I, Fufaev N A. Dynamics of Nonholonomic Systems. Phode Island, Providence: American Mathematical Society, 1972. |
| [13] | Hamel G. Die lagrange-eulersche gleichungen der mechanik. Zeitschrift fr Mathematik und Physik, 1904, 50: 1-57 (in German) |
| [14] | Hamel G. Theoretische Mechanik. Berlin: Springer-Verlag, 1949. (in German) |
| [15] | Cabannes H. General Mechanics (Second edition). Massachusetts, Waltham: Blaisdell/Ginn, 1968. (in English, translated from the original French) |
| [16] | Kirgetov V I. The motion of controlled mechanical systems with prescribed constraints (servoconstraints). Journal of Applied Mathematics and Mechanics, 1967, 31(3): 465-477 (in English, translated from original Russian) |
| [17] | Chen Y H. Constraint-following servo control design for mechanical systems. Journal of Vibration and Control, 2009, 15(3): 369-389 |
| [18] | Moore E H. On the reciprocal of the general algebraic matrix. Bulletin of the American Mathematical Society, 1920, 26: 294-395 |
| [19] | Penrose R. A generalized inverse for matrices. Proceedings of the Cambridge Philosophical Society, 1955, 51: 404-413 |
| [20] | Chen Y H. Second-order constraints for equations of motion of constrained systems. IEEE/ASME Transaction on Mechatronics, 1998, 3(3): 240-248 |
| [21] | Chen Y H. Equations of motion of constrained mechanical systems: given force depends on constraint force. Mechatronics, 1999, 9(4): 411-428 |
| [22] | Rosenberg R M. Analytical Dynamics of Discrete Systems. New York: Plenum Press, 1977. |
| [23] | Papastavridis J G. Analytical Mechanics. New York: Oxford University Press, 2002. |
| [24] | Chen Y H, Leitmann G, Chen J S. Robust control for rigid serial manipulators: a general setting. In: Proceedings of the 1998 American Control Conference. Philadelphia, PA, USA: IEEE, 1998. 912-916 |
| [25] | Udwadia F E, Kalaba R E. On motion. Journal of the Franklin Institute, 1993, 330(3): 571-577 |
| [26] | Bjerhammar A. Rectangular reciprocal matrices with special reference to geodetic calculations. Bulletin Godsique, 1951, 20(1): 188-220 |
| [27] | Baumgarte J. Stabilization of constraints and integrals of motion in dynamical systems. Computer Methods in Applied Mechanics and Engineering, 1972, 1(1): 1-16 |
| [28] | Asada H, Slotine J -J E. Robot Analysis and Control. New York: John Wiley and Sons, 1985. |
| [29] | Slotine J -J E, Li W P. Applied Nonlinear Control. New Jersey: Prentice Hall, 1991. |
 2015, Vol.2
2015, Vol.2 


