2. Mechatronics Embedded Systems and Automation Laboratory, School of Engineering, University of California, Merced, CA 95343, USA;
3. Department of Electrical and Computer Engineering, Utah State University, Logan, UT 84322, USA
As the most socially complex animals on the planet, research related to crowd of pedestrians has received a lot of attention in recent years. A lot of work has been conducted from perspectives of behavior,psychology,cognition and network to analyze problems related to particles,vehicles,robots,animal and even human beings (See [1, 2, 3, 4, 5]). Some manuscripts have been published in recent years concerning the modeling and control problem of crowd of pedestrians such as [6, 7, 8, 9, 10, 11, 12, 13, 14, 15].
On the other side,catastrophic events occurring around the world have demonstrated the need to re-analyze and re-examine current evacuation policies and procedures for crowd of pedestrians. The dynamic and uncertain nature of disasters has required the need of changing backup contingency plans according to evacuation needs. The first problem that confronted in the research of crowd of pedestrians is how to obtain a satisfactory model to characterize the complex nature of this kind of dynamic systems. There are a lot of characteristics which should be considered in the modeling and control problems such as self-organization,following leaders, common motives for action,psychological unity,emotional intensity, level of violence as shown in [16]. Due to features mentioned above, modeling and control of crowd of pedestrians are challenging tasks as shown in recent work of [17, 18, 19, 20, 21, 22].
Recent studies on modeling and control of crowd of pedestrians have been firstly reviewed in this paper in three different scales. Then necessities of introducing fractional calculus in the modeling and control of crowd of pedestrians have been discussed in detail and networked Segways with on-board emergency response personnels have been employed in the evacuation control of crowd of pedestrians. Framework based on cyber-physical systems have been formulated in the end for studying the modeling and control problem of crowd of pedestrians. Main contributions of this paper lie in that the tool of fractional order calculus have been introduced in the modeling and control of crowd of pedestrians where some phenomena observed from realities are impossible or not easy to be considered just in the framework of integer order calculus. The aim of this paper is to provide an alternative way for studying the complex crowd of pedestrians which is much more close to reality.
The rest of the paper is organized as follows. Model for crowd of pedestrians are firstly reviewed in three different scales in Section II respectively; Then recent advances in control of crowd of pedestrians are discussed in micro-scale and macro-scale in Section III; Our framework for studying the evacuation problem of crowd of pedestrians are shown in Section IV based upon calculus of fractional order. Validation of obtained theoretical results are also included in this Section; Conclusions of this paper are given in Section V.
II. MODELING OF CROWD OF PEDESTRIANSA lot of modeling methods have been proposed recently. Most of these modeling methods are based on inspirations that the crowd of pedestrians can be treated as moving particles,smoothing fluids, or granular flows in different scales. Modeling methodologies are firstly reviewed in micro-scale,macro-scale and mesco-scale, respectively. Then necessity of introducing fractional order calculus in the modeling of crowd of pedestrians are discussed and some recent advances of modeling using fractional order calculus are also included in this section.
A. Micro-scale---Ordinary Differential Equation (ODE)When the density of pedestrians is low,each pedestrian can move freely and interactions among pedestrians can be modeled using the framework of social forces. A lot of research has also been conducted using the Newton's laws as shown in the following microscopic model
| \begin{align} m_{i}\frac{{\rm d}v_{i}}{{\rm d}t}=f_{i}^{S}+\sum_{j=1}^{n}f_{ij}^{N}+\sum f_{k}^{W},\label{eq:micro model} \end{align} | (1) |
where $f_{i}^{S}$ is the self-driven force towards some desired velocity,$f_{ij}^{N}$ is the interaction between agent $i$ and its neighbor $j$ and $f_{k}^{W}$ represents the interactions with environment such as walls or corridors.
Different $f_{ij}^{N}$ and $f_{k}^{W}$ have been constructed in the work of [23] for panic scenarios and it has been proved that neither internal forces nor external forces alone can perform well in the evacuation of crowd of pedestrians and the practical way is to consider them simultaneously in the micro-scale model (1); Similarly,it has been shown in [24] that not only external forces such as interactions with neighbours and environments but also some internal forces such as will force and personal information should be considered in the modeling process. But the fact is that a lot of work has been done from the view of multi-agent system where only external forces are considered. Interactions with external environment such as the spatial-temporal markings have been described as potential function and added into the right-side of (1) as done in [25]; Relationship between formation patterns,stability and different interactions have also been analyzed in [26] under external potential function to find whether a swarm will collapse or not. Some recent work such as [27, 28] from the aspect of modeling and [29, 30] from the aspect of control are also only focused on external interactions with neighbouring agents.
Most of the simulation results have been conducted in this scale as shown in [12] because the methods are simple and animations are realistic. In order to satisfy the requirements of high realism and real-time animation in the modeling and control in this scale,the idea of mapping desired behaviors to the stable solutions of classical nonlinear dynamic system such as Van der Pol oscillator or fix-point attractor has been introduced in [31] and [32] where one nonlinear transformation connecting pedestrian's periodic or non-periodic motion with structurally stable system has been firstly constructed and then real-time animation problem can be easily solved in low-dimensional space without losing details; Methods from cognitive science such as heuristic behavior have been employed to adjust the walking direction and speed in micro-scale in [1]; Global roadmap-based navigation method has been proposed in the homing or exploring problem as shown in [33]. Although these methods are simple and efficient,the prescription of all behaviors is not very easy for crowd of pedestrians of large numbers.
Remark 1. Comments on microscopic model:
1) Main advantages of the microscopic model lie in that heterogeneities of each pedestrian can be considered explicitly and simulation results obtained are of highly realistic. But the microscopic model is not a good choice if the number of pedestrians are very high as some unnecessary interactions or effects have been included.
2) Most of the previous work has just treated each pedestrian as one physical particle and few works have been done under the consideration of pedestrian's memory or some other internal effects; Local interacting rules have received a lot of attentions in previous research while long range interacting rules are not so popular.
B. Macro-scale---Partial Differential Equation (PDE)The motion of crowd of pedestrians show some striking analogies with the motion of fluids when the density goes high. Thus research of crowd of pedestrians in macro-scale has benefited a lot from the macro-scale research of traffic system where the well known LWR (Lighthill Whitham and Richards) model (2) and PW (Payne-Whitham) model (3) have been proposed. It is well known that the traffic dynamic system in macro-scale as shown in [14] can be described by
| \begin{align} \frac{\partial}{\partial t}\rho(t,x)+\frac{\partial}{\partial x}f(t,x)=0, \end{align} | (2) |
and
| \begin{align} &\frac{\partial}{\partial t}\rho(t,x)+\frac{\partial}{\partial x}\rho(t,x)v(t,x) =0,\label{eq:PW}\notag\\ & \frac{\partial}{\partial t}v(t,x)+ v(t,x)\frac{\partial}{\partial x}v(t,x) =\frac{V(\rho)- v}{\tau}-\frac{A(\rho)_{x}}{\rho}+\mu\frac{v_{xx}}{\rho}, \end{align} | (3) |
where $\rho$ denotes the density of crowd and $f(t,x)$ is the flux of crowd,$V(\rho)$ is equilibrium Speed,$\frac{V(\rho)-v}{\tau}$ is the relaxation term,$\frac{A(\rho)_{x}}{\rho}$ is the anticipation term and $\mu\frac{v_{xx}}{\rho}$ is the viscosity term. Relationship between flux and density has attracted a lot of interests and a lot of work has been done to generalize the LWR model and PW model.
Two versions of LWR model such as high-order LWR model and low-order LWR model have been shown in [34]. Compared with classical LWR models that only focus on transitions among equilibrium states and homogeneity,both non-equilibrium transitions and inhomogeneities have been accommodated in the work of [34] through constructing much more complex relationship between flux and density; Similarly,new relationship between speed and density has been used to derive Lighthill-Whitham model in panic scenarios in [35].
Also based on the fundamental conservation law of mass and momentum, macroscopic model for crowd pedestrians in two dimensional space, as below
| \begin{align} \frac{\partial}{\partial t}\rho+\frac{\partial}{\partial x}(\rho u)+\frac{\partial}{\partial y}(\rho y)=0\label{eq:Roger model} \end{align} | (4) |
has been constructed in [36] for different types of pedestrians with different walking habits. Macroscopic model in two dimensional space has been generalized in [37] with additional terms for anticipation and relaxation.
As interactions among pedestrians are assumed to be the same in macro-scale,it is not easy to incorporate the heterogeneities of each pedestrian. In order to characterize the crowd of pedestrians more precisely,models that can benefit from both the micro-scale and macro-scale are much preferred. A modeling procedure based on the time-varying measures
| \begin{align} \mu_{t}=\theta m_{t}+(1-\theta)M_{t} \end{align} | (5) |
has been prescribed for the multi-scale characterization of crowd-pedestrian system where $m_{t}=\sum_{j=1}^{N}\delta P_{j}(t)$ and ${\rm d}M_{t}(x)$ $=$ $\rho(t,x){\rm d}x$ are the microscopic and macroscopic mass respectively. Both topological interactions such as the Braess's paradox (obstacles may contribute to improve the flow of people in some situations) characterized in macro scale and anisotropic interactions such as the granular role of some pedestrians described in micro-scale can also be considered in this framework through the time-varying measure (5); Similar results that are composed of agent-based microscopic model and flow-based macroscopic model have been shown in [38] and [39] where the accuracy of microscopic model and the efficiency of macroscopic model have been combined together through initializing each other by techniques of aggregation and disaggregation.
Remark 2. Comments on macroscopic model:
1) Computation time have been greatly decreased as each pedestrian has been treated as physical particle and has same characteristics in macro-scale.
2) Main disadvantages of macroscopic models lie in that heterogeneities of pedestrians such as interactions or mobilities cannot be characterized or considered in detail in this scale. Obtained results using the macroscopic model just provide some references for the control of crowd of pedestrians.
C. Mesco-scale---Integral Differential Equation (IDE)After Boltzmann formalized the concepts of kinetic equations in the nineteenth century,it has been widely used in astrophysics, engineering,social science and even biology. Although the following basic kinetic-transport equation
| \begin{align} \frac{\partial}{\partial t}f(t,x,\xi)+\xi\cdot\nabla_{x}f(t,x,\xi)=0\label{eq:mesco equation} \end{align} | (6) |
that describes the evolution of density $f(t,x,\xi)$ of particles passing through $(t,x)$ with velocity $\xi$ seems very simple,great success has been achieved in the applications of Boltzmann's kinetic equation and many generalizations of this equation have been made.
A lot of modeling results for crowd of pedestrians have been derived from the equation (6) since macro-scale variables and micro-scale variables have been combined with each other in this equation. Nonlinear integral-differential equations have also been used in [40] to describe the {crowd of pedestrians} with competitions and kinetic interactions as
\begin{align*} \frac{\partial f_{i}}{\partial t}(t,u)=J_{i}[f](t,u)+\gamma_{i}(t,u), \end{align*}
where the $J_{i}[f](t,u)$ describes the evolution of density due to gain and loss of distribution function and $\gamma_{i}(t,u)$ describes the production and migration of the group; Mescoscopic models with binary interactions,averaged binary interactions and mean field interactions have been given in [41] as
| \begin{align} \frac{\partial f}{\partial t}+\xi\frac{\partial f}{\partial x}+\frac{\partial(fF[f])}{\partial\xi}=Q(f,u),\label{eq:Bellomo} \end{align} | (7) |
where different $F[f]$ and $Q(f,u)$ are employed to describe these interactions. Conservation law of mass and momentum in macro-scale has been generalized in [42] where internal intentions and external interactions have been simultaneously considered in the following mescoscopic model
| \begin{align} &\frac{\partial}{\partial t}\rho_{\mu}+\frac{\partial}{\partial x}(\rho_{\mu}v_{\mu}) \nonumber \\ &\qquad =\int m_{\mu}q_{\mu} {\rm d}v_{\mu}+ \sum_{\mu}\left[\frac{m_{\mu}}{m_{v}}\rho_{v}\chi_{\mu}^{\mu v}(1)-\rho_{\mu} \chi_{\mu}^{\mu v}(1)\right], \end{align} | (8) |
where $\rho_{\mu}$ is the density,the first term on the right is caused by pedestrians entering or leaving some interested areas and the second term describes the effects caused by internal intentions and external interactions. Equation (8) has been generalized to the following two dimensional mescoscopic equation
\begin{align*} &\partial_{t}\rho+[\partial_{x_{1}}(\rho v_{1})+\partial_{x_{2}}(\rho v_{2})] + [\partial_{v_{1}}(\rho A_{1})+\partial_{v_{2}}(\rho A_{2})]\\ &\quad\ = (\partial_{t}\rho)_{\rm event}^{+}-(\partial_{t}\rho)_{\rm event}^{-} \end{align*}
in [43] where $\partial_{x_{1}}(\rho v_{1})+\partial_{x_{2}}(\rho v_{2})$ means the changes of density due to convection, $\partial_{v_{1}}(\rho A_{1})+\partial_{v_{2}}(\rho A_{2})$ are the terms of acceleration and deceleration,$(\partial_{t}\rho)_{\rm event}^{+}-(\partial_{t}\rho)_{\rm event}^{-}$ means the interaction of events.
Some other research have also been conducted from the aspect of micro-scale using the framework of mesco kinetic theory. With the help of activity variables,heterogeneities of each pedestrian have been characterized in micro-scale in [44] and [45] using the statistical distribution of position and velocity; Enskog-like interactions and stochastic interactions have been considered in [46]; Nonlinear interactions instead of linear interactions have been applied in [47]; Both short and long range interactions have been reported in [44] contrary to previous modeling methods where only local interactions are assumed.
Remark 3. Comments on mescoscopic model:
1) As both information from micro-scale and information from macro-scale have been included in this framework,heterogeneities of pedestrians and different kinds of interactions can be included easily in the right hand side of (7); Another advantage is that efficiency of the mescoscopic model has been greatly improved compared with that of microscopic model.
2) One of the main disadvantages of mescoscopic model is that existence of analytic expressions for equilibrium is not guaranteed for obtained IDEs and another disadvantage of this framework is the technical difficulty when there are more than one microscopic variables that needed to be included in the above IDEs.
D. Fractional ModelFractional Calculus has shown great potential in different applications such as particles in fluid,plasma physics,quantum optics and many others. Some phenomena such as self-similarity, non-stationary and spiky phenomena,non-Gaussian relaxation,short or long memory and long range interactions are all closely related to fractional calculus. The authors have noticed that previous research has mentioned or implied potential applications of fractional calculus in modeling,control and optimization of {crowd of pedestrians} in different aspects such as description of motion, description of interactions and hysteresis phenomenona. Recent advances in these aspects are shortly reviewed in the followings.
1) Fractional calculus in description of motion
Some applications of fractional calculus has been done for physical particles in macro scale. Based on the fractional derivative of order $\alpha$ in [48]
| \begin{align} \frac{\partial^{\alpha}f(x,t)}{\partial t^{\alpha}}=\underset{\triangle t\rightarrow0}{\lim}\frac{f(x,t+\triangle t)-f(x,t)}{\triangle t^{\alpha}},\label{eq:definition fractal order} \end{align} | (9) |
some different fractional kinetic equations (FKE) and their properties have been explained in [49] such as the FKE with desired direction,anisotropic FKE and nonlinear FKE; Then fractional kinetics of distributed-order has been proposed in [50] and it has been shown that the fractional model with distributed order can be effectively used to describe the accelerating and decelerating of sub-diffusion and super-diffusion. Based on these preliminary works,fractional model for crowd of pedestrians in the macro-scale has been proposed in [51] using the fractal derivatives of time and space where fractional order dynamics for one dimensional crowd can be described as
| \begin{align} \frac{\partial}{\partial t^{\alpha}}\rho(t,x)+\frac{\partial}{\partial x^{\beta}}[\rho(t,x)v(t,x)]=0,\label{eq:my frac model} \end{align} | (10) |
where $\rho\text{(t,x)}$ and $v(t,x)$ are the density and velocity of crowd at position $x$ and time $t$,$\alpha$ and $\beta$ is the fractal order of time and space respectively. Similar results can also be found in [52] where $\alpha=\beta$ has been assumed. Considering that each pedestrian's decision making process plays an important role in his (her) next movement,the dynamic process of decision making has been described in [21] where coupling dynamic models composed of the fractional Fokker-Planck equation
| \begin{align} \frac{\partial^{\alpha}P(u,t)}{\partial t^{\alpha}}=-\frac{\partial[f(u,d,t)P(u,t)]}{\partial u}+\Xi(P,u,t),\label{eq:forward} \end{align} | (11) |
and the fractional master equation
| \begin{align} \frac{\partial^{\alpha}u(x,y,t)}{\partial t^{\alpha}}=f(u,d,t)+g(u,d,t)\xi(t)+\eta(t)\label{eq:backward} \end{align} | (12) |
have been constructed and $P(u,t)$ is the distribution function, $\Xi(P,u,t)$ is the additional terms due to variations in infinitesimal time increment,$u(x,y,t)$ defines the cost that each pedestrian should pay for his desired destinations,$f(u,d,t)$ is the nonlinear dependence on previous costs $u(x,y,t)$ and previous decisions $d(t)$. The forward dynamics (11) describes the evolution of distribution function with respect to time while the backward equation (12) describes the evolution of pedestrian's decision with respect to the inverse of time. In order to control and predict the evolution of crowd of pedestrians,optimal control of this complex system has been firstly reformulated in [53] based on the fractional master equations.
Concerning the fractional model in micro-scale,fractional Langevin equations have been given in [54] for human motion tracking while fractional models with fixed order and variable order have been proposed in [55] and [56] to describe motion of pedestrians.
Different formation patterns for swarming of fish can be generated through tuning the area of attraction and repulsion as shown in [57]; Quantitatively characterizing of relationship between the area of repulsion and attraction have been analyzed in [58] for dynamic model of integer order. Thus even for dynamic models of integer order,phenomena of transiting from ordered state to disordered state have been observed in [59] under long range interactions. Transition from chaos to turbulence has been reported in [60] where fractional long range interactions of $\frac{1}{l^{1+\alpha}}$ ($l$ is the distance between oscillators,$\alpha$ is the tuning parameter) has been imposed for nonlinear oscillators. Recently, transitions have also been declared for Boltzmann equations using local,non-local or configuration-dependent interactions in [61] where transition from purely diffusive regime to flocking patterns can be realized by modulating the range and strength of interactions. From which we can say that range of interaction and strength of interaction play an important role in study of system of large numbers.
Actually,the long range interactions are connected with fractional dynamics. Relationships between long range interactions of power law in micro-scale and fractional Euler-Lagrange equations in macro-scale have been discussed in [62] and it has been proved that there exists one fractional Euler-Lagrange equation in macro-scale if there are long range interactions of power law in micro-scale; From which we can say that the gap between micro-scale and macro-scale can be bridged together using long range interactions of power laws. As the long range interactions are so common in crowd of pedestrians,it is reasonable to describe the dynamics of crowd of pedestrians using fractional calculus.
3) Hysteresis phenomenon and collective memory
It has been shown in [57] that minor changes in individual's responses can lead to different collective behaviors such as alignment,swarm and torus where the collective memory has played an important role; Hysteresis phenomenon has been observed in [4] where nonlinear relationship between collective behaviors and range of interactions has been explicitly shown in Fig. 1 of [4].

|
Download:
|
| Fig. 1. A cyber physical framework for describing the coupling of model, control, and management. | |
According to the following definition of Hysteresis from Wikipedia: Hysteresis is the dependence of the output of a system not only on its current input,but also on its history of past inputs. In other words,the change of group's behavior not only depends on the current control input but also depends on the history of individual behavior and the shape of group; The hysteresis phenomenons or effects of short memory are so common that they can be found in the acceleration,deceleration and equilibrium of traffic flows in [63] and individual's actions such as buying and selling in the stock market. For particles with long time memory,fractional Fokker-Planck equations have been derived in [64] based on the correlating functions of probability densities that is power law; A non-negative memory function $\eta(\cdot)$ has been introduced in [65] to generalize the LWR model using the form of convolution
$ \rho\ast\eta=\int_{R^{2}}\eta(x-\xi)\rho(t,\xi){\rm d}\xi, $
where preferred path can be found and regions of high density can be avoided.
As calculus of integer order can be considered as special case of fractional order calculus,each pedestrian can be characterized much closer to reality using the framework of fractional order calculus. Many effects such as individual's memory,long-range interactions which are difficult to characterize using calculus of integer order can be compensated using calculus of fractional order.
Remark 4. Compared with dynamic models of integer order in previous research,some advantages and disadvantages of dynamic model of fractional order are listed in the followings:
1) In time domain: Only normal diffusive process has been considered in previous study in macro scale due to the limitation of calculus of integer order. Besides the normal diffusive process, sub-diffusive process and super-diffusive process can be added to describe the crowd in macro scale using fractional calculus in time domain.
2) In spatial domain: Dimension of space are only limited to 1,2 or 3 in previous research while fractional dimension of space can be easily included using fractional order calculus for considering effects of environments.
3) Some other elements: As we have shown that some phenomenons such as self-similarity,non-stationary and spiky phenomenons, non-Gaussian relaxation,effects of memory,long-range interactions which are difficult to characterize or explain using calculus of integer order can be compensated using calculus of fractional order.
The authors do not want to prove that previous models of integer order are not effective anymore in reality and we just want show that fractional calculus as generalization of calculus of integer order has provided us much more freedom in characterizing and understanding of the complexities of crowd of pedestrians. The authors admit that there are a lot of challenging work left to do for the obtained model of fractional order such as controller design,stability analysis and performance evaluation. Most of them are not so easy to solve now.
III. CONTROL OF CROWD OF PEDESTRIANS A. Control of Macroscopic ModelIn the evacuation of crowd-pedestrian system,moving direction and moving speed are of great importance to guarantee the smooth movement of crowds. Some previous research has chosen $v(t,x)$ in (3) as the control input and distributed state feedback controllers have been constructed in [66] and [67] for the macro-scale model in one and two dimensional space. Main idea of [66] and [67] is using finite dimensional system to approximate infinite dimensional system; Then theory of nonlinear control can be used for design of feedback controllers for this approximating system. Main problems of this framework is that the original system may be still unstable even if the obtained controllers work very well on the approximating system. Different from the framework of approximation,the control and stability problem of the macroscopic model (3) has been formulated directly in the distributed control of partial differential equations in [68] and [69]. Previous controllers have been generalized to diffusion, advective and advective-diffusion controllers. Comparisons of these controllers have been done in [70] and it has been shown that much more serious problems may arise if only diffusion feedback controller is adopted as there is no preferred direction for the pedestrians to follow in evacuation process; But faster evacuation can be realized for LWR model under diffusion-advection-state feedback controllers since the direction of evacuation is provided.
In order to avoid undesirable congestion and blockages in the evacuation of pedestrians,optimal feedback controllers have been proposed in [71] and [72] by instructing pedestrians to adjust their velocities. Although optimal results have been obtained in [71] and [72],applications of these results are only limited the deterministic case. Robust control of crowd-pedestrian system has interested a lot of people in recent years. For example,Lyapunov techniques have been firstly utilized in [73] to construct velocity controllers for automated highway systems where not only position and time but also effects of lanes,drivers and destinations have been included in the macroscopic PDE model; Previous diffusion-state feedback controllers have been generalized using methods of Lyapunov redesign in [74] to deal with disturbances in control input; Robust controllers based on sliding model control have been constructed in [75] for the control of crowd of pedestrians with matched and unmatched uncertainties that are caused by external disturbance and parametric variations.
Remark 5. Similar to the modeling methods for macroscopic model,heterogeneities of controllers have also been neglected in this scale.
B. Control of Microscopic Model1) Control using leaders with naive followers: Based on inspirations from swarming of ants,schooling of fish and flocking of birds,how to formulate or control the collective behaviors in micro-scale has received a lot of attentions from the community of control,computation and computer. One of the fascinating phenomenon is that this kind of collective behaviors can be generated from simple or basic interacting rules and control of this kind of collective behaviors can be realized through controlling just a small part of the group.
Determining of moving direction based on neighbor's direction have been firstly proposed in [76] for average consensus problem of each agent. Work of [5] and [4] has explicitly shown the quantitative relationship between individual's local interacting rules and group's collective behaviors; Three experiments have been done in [77] to show the effects of number and topology of informed agents on the consensus problem and it has been proved using experiments that only a small number of informed individuals are enough for driving a large number of uninformed individuals to reach consensus without explicit communications; Further results concerning consensus under uncertain or conflicting information have been considered in [78]. For evacuation problem of crowd pedestrian system,result of [79] has shown that the evacuation rate can be greatly improved by adding some leaders with global knowledge and it is always good for the evacuation process if we place some leaders in the immediate proximate of crowds and some leaders scattered around the environment.
Remark 6. Similar to the pinning control of complex network with large number of nodes,how many nodes are needed to control the network and which one should be chosen as the pinning node are interesting problems. For crowds,how many leaders and what kind of leaders are needed in control of crowd of pedestrians are worthy of further considerations.
Phenomena such as self-similar structure,heavy-tailed workloads and long-range dependence effects that have been proposed in [80, 81] for study of network are related to calculus of fractional order. The authors think that not only topology and connectivity should be considered but also the dynamic evolutions of the network itself should be considered especially when confronted with stochastic network of large numbers. Thus control in the framework of fractional order calculus is very interesting although there are many challenges.
2) Control without leaders:
a) Decentralized framework
Using the methodology of decomposition,control problems for complex system can be transformed into control problems for simpler subsystems. A lot of decentralized controllers have been obtained using the framework of decomposition. Decentralized controllers for large number of stochastic agents have been given in [82] where not only the evolution in time scale but also the evolvement in ``space'' scale (where $N\rightarrow\infty$,$N$ is the number of agents) are considered; Decentralized controllers have also been constructed using the framework of decomposition in [83] where complex LQG games problem has been reduced to two-player games problem.
Advantages of the decentralized framework are that the burden of computation has been greatly reduced and obtained results can be easily extended to systems with large numbers. However,neighbor's information is not used in the decentralized framework,where it is much preferred to use distributed controllers.
b) Distributed framework
Some other distributed feedback controllers for macroscopic model have been reviewed in previous sections or can be found in [67, 68, 69]. Some consensus protocols of multi-agent system also belong to this framework which we will not state one by one and interested readers can find some recent advances in the review papers of [84, 85] or references in them.
One big challenge for distributed control lies in the burden of computation if the number of pedestrians goes to infinity. Some previous research has adopted the mean field methods to estimate the influence of neighboring agents to relieve the burden of computation. Mean field methods have been used in [86] for controller design for leader-follower agents of linear stochastic dynamics; Distributed controllers for agents with one major/leader agent have been given in [87] with Markov jump parameters in controlled system and random parameters in objective functions where mean field method has been utilized to estimate effects from neighboring pedestrians and the leader; Mean field LQG controllers have been proposed in [88] for socially optimal control problem whose cost functions are coupled with each other; Mean field control strategies have been given in [89] for the consensus problem of multi-stochastic agents based on the assumption that information of initial state distribution is available to each agent; Similar results can also be found in [90] in the control of stochastic multi-agent systems where statistical information of neighboring agents are obtained using mean field methods.
In order to study the true interacting rules among agents,game theory has also been combined with mean field method in control of agents of large numbers which we will call it mean field games in the followings. Based on mean field games introduced in [91], dynamics of human's decision making process has been considered in [92] where mean field game theory has been employed in the backward Hamilton-Jacobi-Bellman (HJB) equation and forward Fokker-Plank (FP) equation; The forward-backward equations have also been adopted in [93] to describe the aversion and congestion phenomena in macroscopic scale where each pedestrian's ability of anticipation has been characterized using the backward equation.
Advantages of the mean field method is that only information of initial distributions is needed in the design of controllers and the popular topology condition such as connected graph or jointly-connected graph is no longer needed; Additional benefit is that communications among neighboring individuals are no longer needed and obtained results can also be easily extended to systems with large numbers.
Remark 7. Research of crowd of pedestrians has benefit a lot from the research of traffic control system where limiting speed has served as an effective way to guarantee the normal flow of vehicles. Information of density has been used in specifying limitation of speeds in different area in [14]. Roadmap-based planning has been used in [28] for evacuation of large number of agents where interactions and coordination among agents are of great importance in realization of the evacuation.
Speed,density and even interactions are main concernings that have received a lot of attention from the view of multi agent system. Besides the above mentioned,it is the authors' belief that effects of memory,environment or even building structure should be considered in modeling and control of crowd of pedestrians where fractional calculus will play an important rule.
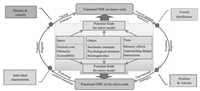
IV. OUR FRAMEWORKA fractional framework for modeling and controlling of crowd of pedestrians has been proposed in this paper. The proposed research represents the coupling of the ``PHYSICAL PART'' (mass pedestrian evacuation management of crowds) with the ``CYBER PART'' (modeling and prediction of crowds). And transferring of information between these two parts has been implemented through networked Segways,with on-board emergency response personnels,and facility sensing and actuation.
In cyber part,ordinary differential equations,partial differential equations and integral differential equations have been employed to describe the crowd of pedestrians using calculus of fractional order in micro-scale,macro-scale and mesco-scale,respectively. Interesting information such as speed,density,flux and even formation patterns are obtained through CCTV. Segways,Cellphone and some other sensors can be used in calculating the obtained models,controlling the crowds and even predicting the stampede that is going to occur. Closed loop system that composed by the cyber part and physical part in Fig. 1 has shown the flow of information and major points of each part.
A. Fractional Modeling of Crowd of Pedestrians1) In micro-scale level with low density of crowds,behavior of each pedestrian can be described by the ordinary differential equations based on some widely used methods such as social force model (1) or agent based model where parameters of systems can be further calibrated using empirical or observed data. Main reason of using these classical models is due to the convenience of introducing heterogeneities in the description of pedestrians in micro-scale.
2) In macro-scale level,the density of crowds is so high that the motion of all pedestrians can be modeled as continuum fluids where partial differential equations can be derived from the conservation law of mass or momentum on interested area. Main differences between crowd of pedestrians and smoothing fluids are that different motion patterns such as crossing or intersecting is allowed in crowd-pedestrian system due to the freedom of choosing different routes. The authors believe that both the time scale and the spatial scale should be considered in the modeling of crowd of pedestrians and preliminary work of fractional macroscopic model (10) has been shown in [51] where the fractional order associated with time and the fractional order associated with the fractal structure have been included.
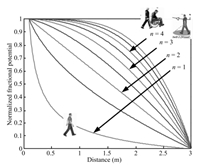
3) In mesco-scale level with medium density,the dynamics of evacuation or egress process is similar to the diffusion process of active particles in many aspects such as the porous or granular pattern in the smoothing fluids. Fractional convection-diffusion equations are useful tools to model the crowd pedestrians in this case due to the phenomenon of porosity observed in this scale; Heterogeneous pedestrians can be modeled using mobile potential fields indexed by {activity variables} as shown in Fig. 2 which can be included in the convection-diffusion equations to guarantee the existence of heterogeneities on this level; Interactions between microscopic model and macroscopic model can also be realized through mean field games to increase the validation of obtained models and relieve the burden of computation. Reasons of using the above modeling framework as follows.
|
Download:
|
| Fig. 2. Normalized effect of activity variables on potential fields (PFS). | |
a) As there is no general method prescribed for modeling crowd pedestrians for all kinds of scenarios,it is much reasonable to choose the most appropriate model for different problems. Since the microscopic model is powerful to describe the heterogeneities of pedestrians,we choose to use the microscopic model when the density is low; With the increasing of density,granular flows with porosity phenomenon can be observed in large crowds. This kind of heterogeneities are modeled using different mobile potential fields which can be easily added into the right hand side of (7) to describe the effects from micro-scale; As density grows,the porosity or granular phenomenon of smoothing fluids disappears and fractional dynamic model can also be obtained by using generalized conservation law of mass or momentum as deduced in previous section.
b) The macroscopic model is responsible for generating a homogenizing effect with desirable smoothness in macro-scale,and the microscopic model is responsible for characterizing heterogeneities and interactions from the macro-scale. For mescoscopic model,not only heterogeneities and porous patterns of crowds can be explicitly characterized but also interactions between micro-scale and macro-scale can be included in the obtained integral differential equations.
c) Although we describe the modeling of crowds in different scales according to their densities,these obtained models are not independent of each other as shown in Fig. 3. The macro-scale variables such as density or flow comes from aggregation of micro-scale data of each pedestrian and the motion of each pedestrian is also affected or constrained by the people around him.
|
Download:
|
| Fig. 3. Fractional model in micro-scale and macro-scale. | |
1) In microscopic level,the control of each pedestrian is focused on analyzing the relationship between different interactions and collective patterns where not only interactions based on topology but also interactions based on short range and long range interactions will be considered. Dynamics of crowd-pedestrian system under long range interactions are closely related to fractional calculus and have an important effect on generation of different collective patterns.
This phenomenon observed from self-organized groups under different interactions can be used to control the collective motion of crowds where mobile Segways have been added into the group to tune range of interactions among pedestrians to generate some desired collective patterns.
2) In macroscopic level,fractional controllers based on fractional convection,diffusion or both of them will be constructed for controlling of the smoothing fluids (10) for crowd of pedestrians with fractional time/spatial orders.
Due to the high densities in this scale,it is not easy to inject control agents into the fluids. In our framework,mobile Segways with emergency personnels will be dispatched to control the inflow and outflow of crowds from outside based on the theory of boundary control to guarantee the smoothing evacuation of high-density crowds without breakdowns.
3) In mescoscopic level,forward fractional convection-diffusion equations and backward fractional Hamilton-Jacobi-Bellman (H-J-B) equations are used for modeling the crowd of pedestrians where the forward part describes the evolution of crowds and the backward equation describes the evolution of decision making process.
a) Movement of next step will be prescribed based on the probability distribution function as shown in backward part (12) of the fractional HJB equations.
b) Fractional order controllers based on fractional diffusions or fractional convections are adopted to realize the control or optimization of the forward part (11) of the fractional HJB equations.
c) Mean field games will play an important role in estimating neighbor's influence and reducing burden of communication and computation.
d) Mobile Segways with global instructions can be used to guide or drive the crowds through broadcasting or changing the structure of space to control the velocity or flow of the crowds.
Reasons of using the above control framework as follows.
1) For crowds with low density,mobile Segways can be easily added into the crowds and control of the crowd-pedestrian system can be realized through interactions with just a few of them to realize control of each pedestrian.
2) For crowds of high density,it is not wise to inject mobile Segways into the crowds again due to the high density. In this case, movements of pedestrians are firmly constrained by the people around them. What we try do is using more delicate controllers such as boundary control to tune the inflow and outflow of people through Segways to realize the smoothing fluids without breakdowns.
3) For crowds with medium density,there are some concerns that are not easy to be solved in this scale. Besides heterogeneities and computation burdens,the interactions between microscopic model and macroscopic model are the main challenges. In other words,balancing between realization of each pedestrian's target and desired evolution of the entire group can be manipulated simultaneously in the framework of dynamic game theory based on mean field.
C. Platform for VerificationSince real verifications of the theoretical results for evacuation of crowd of pedestrians are not easy to conduct,a lot of simulation results have been done in previous research. There are a lot of software for the simulation research such as VISSIM,EXODUS,Simulex,PSCrowd, PEDSIM,and VISWALK,et al.
1) VISSIM is one powerful tool available for simulating multi-modal traffic flows,including cars,buses,motorcycles,bicycles and pedestrians and it is also a useful tool for the evaluation of various alternatives based on transportation engineering. In VISSIM, movement of each pedestrian is modeled by the social force model$^{[94]}$ where a total force resulting from the social, psychological,and physical forces has been imposed. The forces that are influencing pedestrian's motion are caused by his/her intentions to reach his destination as well as by other pedestrians and obstacles. Thereby the other pedestrians can have both attractive and a repulsive influences.
2) Due to the requirements of data processing and computations in modeling and control of crowd of pedestrians,the simulation research is much preferred to be realized using Matlab. The authors of this paper try to study the modeling and control problem using the platform of DIFF-MAS that has been developed in [95] for simulating the measurements and control of diffusion processes using Matlab script and Simulink. Optimal placements of sensors and actuators,and structures for understanding distributed networked actuation and sensing have been done on this platform. Recently,this platform has been updated for measuring and control of diffusive process of fractional order which is useful for modeling and control crowds of pedestrians using calculus of fractional order.
Remark 8. Considering unexpected or dangerous events in real-life experiment,only initial theoretical results and some simple simulation results have been done by the authors under the framework of fractional order modeling and control of crowd of pedestrians. There are lots of work left to show the effectiveness of this framework in future especially from the aspect of control.
V. CONCLUSIONRecent advances in modeling and control of crowd of pedestrians have been reviewed in the framework of cyber-physical systems. In the first part,not only modeling methods in micro-scale,macro-scale and mesco-scale are reviewed but also possibilities of applying fractional calculus are discussed; Due to challenges in the control problem,only controllers in macro-scale and micro-scale have been surveyed such as state feedback controllers,distributed controllers and robust controllers. Initial considerations about control of crowd of pedestrians are discussed in the framework of cyber-physical systems. Long range interactions are used to generate self-organized collective behavior in the micro-scale; Fractional diffusion-convection controllers will be constructed for crowd fluids with fractal time-spatial orders in the macro-scale; Fractional mean field games theory will be adopted in modeling pedestrian's decision making process and control the fluids of crowd with porosity in mesco-scale. Multiple mobile Segways with onboard emergency response personnels are employed to realize the control of velocity and flux of crowd of pedestrians in different scenarios.
A lot of problems are still open and needing cooperation of multi-disciplines such as environmental design,engineering,and transportation. Potential topics such as modeling the crowd of pedestrians with consideration of stochastic noise,psychological effects and constructing controllers under requirements of scalability and robustness are both interesting topics and worthy of much efforts in future. Another interesting and important topic is concerning the security problem in the crowd of pedestrians where some recent results on security of consensus problem such as [96, 97, 98] are beneficial to solve of this problem.
| [1] | Moussaid M, Helbing D, Theraulaz G. How simple rules determine pedestrian behavior and crowd disasters. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(17):6884-6888 |
| [2] | Czirók A, Barabási A L, Vicsek T. Collective motion of self-propelled particles:kinetic phase transition in one dimension. Physical Review Letters, 1999, 82(1):209-212 |
| [3] | Spieser K, Davison D E. Multi-agent stabilisation of the psychological dynamics of one-dimensional crowds. Automatica, 2009, 45(3):657-664 |
| [4] | Couzin I D. Collective cognition in animal groups. Trends in Cognitive Sciences, 2009, 13(1):36-43 |
| [5] | Couzin I D, Krause J, Franks N R, Levin S A. Effective leadership and decisionmaking in animal groups on the move. Nature, 2005, 433(7025):513-516 |
| [6] | Alfio Q, Alessandro V. Analysis of a geometrical multiscale model based on the coupling of ODES and PDES for blood flow simulations. Multiscale Modeling and Simulation, 2003, 1(2):173-195 |
| [7] | Haken H. Information and Self-Organization:A Macroscopic Approach to Complex Systems. Berlin:Springer-Verlag, 2006. |
| [8] | Daniel T, Musse S R. Crowd Simulation. Berlin:Springer-Verlag, 2007. |
| [9] | Peacock R D, Kuligowski E D, Averill J D. Pedestrian and Evacuation Dynamics. Berlin:Springer-Verlag, 2010. |
| [10] | Bellomo N. Modeling Complex Living Systems:A Kinetic Theory and Stochastic Game Approach. New York:Birkhauser Boston, 2008. |
| [11] | Kachroo P, Al-nasur S J, Wadoo S A, Shende A. Pedestrian Dynamics:Feedback Control of Crowd Evacuation. Berlin:Springer-Verlag, 2008. |
| [12] | Pelechano N, Allbeck J M, Badler N I. Virtual Crowds Methods, Simulation, and Control. New York:Morgan and Claypool Publishers, 2008. |
| [13] | Timmermans H. Pedestrian Behavior:Models, Data Collection and Applications. New York:Emerald Group Publishing Limited, 2009. |
| [14] | Kachroo P. Pedestrian Dynamics Mathematical Theory and Evacuation Control. New York:CRC Press, Taylor and Francis Group, 2009. |
| [15] | Barcelo J. Fundamentals of Traffic Simulation. Berlin:Springer Science and Business Media, 2010. |
| [16] | Berlonghi A E. Understanding and planning for different spectator crowds. Safety Science, 1995, 18(4):239-247 |
| [17] | Helbing D, Buzna L, Johansson A, Werner T. Self-organized pedestrian crowd dynamics:experiments, simulations, and design solutions. Transportation Science, 2005, 39(1):1-24 |
| [18] | Bellomo N, Bianca C, Coscia V. On the modeling of crowd dynamics:an overview and research perspectives. SeMA Journal, 2013, 54(1):25-46 |
| [19] | Cristiani E, Piccoli B, Tosin A. Multiscale modeling of granular flows with application to crowd dynamics. Multiscale Modeling and Simulation, 2011, 9(1):155-182 |
| [20] | Christian D. Applicable thermostatted models to crowd dynamics:comment on "thermostatted kinetic equations as models for complex systems in physics and life sciences" by Carlo Bianca. Physics of Life Reviews, 2012, 9(4):410-412 |
| [21] | Bogdan P, Marculescu R. A fractional calculus approach to modeling fractal dynamic games. In:Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, FL:IEEE, 2011. 255-260 |
| [22] | Stuart D, Christensen K, Chen A, Cao K C, Zeng C B, Chen Y Q. A framework for modeling and managing mass pedestrian evacuations involving individuals with disabilities:networked segways as mobile sensors and actuators. In:Proceedings of the 2013 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. 2013. DETC2013-12652 |
| [23] | Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature, 2000, 407(6803):487-490 |
| [24] | Löhner R. On the modeling of pedestrian motion. Applied Mathematical Modelling, 2010, 34(2):366-382 |
| [25] | Dirk H, Schweitzer F, Keltsch J, Molnar P. Active walker model for the formation of human and animal trail systems. Physical Review E, 1998, 56(3):2527-2539 |
| [26] | Orsogna M R D, Chuang Y L, Bertozzi A L, Chayes L S. Self-propelled particles with soft-core interactions patterns, stability, and collapse. Physical Review Letters, 2006, 96(10):104302:1-4 |
| [27] | Song Y Q, Gong J H, Niu L, Li Y, Jiang Y R, Zhang W L, Cui T J. A grid-based spatial data model for the simulation and analysis of individual behaviours in micro-spatial environments. Simulation Modelling Practice and Theory, 2013, 38:58-68 |
| [28] | Rodriguez S O. Roadmap-Based Techniques for Modeling Group Behaviors in Multi-Agent Systems[Ph. D. dissertation], Texas A and M University, USA, 2012. |
| [29] | Wang B C, Zhang J F. Mean field games for large-population multiagent systems with Markov jump parameters. SIAM Journal on Control and Optimization, 2012, 50(4):2308-2334 |
| [30] | Li T, Zhang J F. Asymptotically optimal decentralized control for large population stochastic multiagent systems. IEEE Transactions on Automatic Control, 2008, 53(7):1643-1660 |
| [31] | Giese M A, Mukovskiy A, Park A N, Omlor L, Slotine J J E. Real-time synthesis of body movements based on learned primitives. Visual motion analysis. In:Proceedings of the 2009 International Dagstuhl Seminar Statistical and Geometrical Approaches to Visual Motion Analysis. Berlin:Springer-Verlag, 2009, 5604:107-127 |
| [32] | Mukovskiy A, Slotine J J E, Giese M A. Dynamically stable control of articulated crowds. Journal of Computational Science, 2013, 4(4):304-310 |
| [33] | Burchan B O, Lien J M, Amato N M. Better group behaviors using rule-based roadmaps. In:Proceedings of the 2004 Springer Tracts in Advanced Robotics. Berlin:Springer-Verlag, 2004. 95-112 |
| [34] | Zhang H M. New perspectives on continuum traffic flow models. Networks and Spatial Economics, 2001, 1(1-2):9-33 |
| [35] | Colombo R M, Goatin P, Rosini M D. A macroscopic model for pedestrian flows in panic situations. International Series Mathematical Sciences and Applications, 2010, 32:255-272 |
| [36] | Hughes R L. A continuum theory for the flow of pedestrians. Transportation Research Part B:Methodological, 2002, 36(6):507-535 |
| [37] | Jiang Y Q, Zhang P, Wong S C, Liu R X. A higher-order macroscopic model for pedestrian flows. Physica A:Statistical Mechanics and Its Applications, 2010, 389(21):4623-4635 |
| [38] | Xiong M Z, Cai W T, Zhou S P, Low M Y H, Tian F, Chen D, Ong D W Z, Hamilton B D. A case study of multi-resolution modeling for crowd simulation. In:Proceedings of the 2009 Simulation Multiconference. San Diego, California, USA:IEEE, 2009. |
| [39] | Xiong M Z, Lees M, Cai W T, Zhou S P, Low M Y H. Hybrid modelling of crowd simulation. Procedia Computer Science, 2010, 1(1):57-65 |
| [40] | Arlotti L, Bellomo N, Lachowicz M. Kinetic equations modelling population dynamics. Transport Theory and Statistical Physics, 2000, 29(1-2):125-139 |
| [41] | Bellomo N, Delitala M, Coscia V. On the mathematical theory of vehicular traffic flow I. fluid dynamic and kinetic modelling. Mathematical Models and Methods in Applied Sciences, 2002, 12(12):1801-1843 |
| [42] | Dirk H. A fluid dynamic model for the movement of pedestrians. Complex Systems, 1992, 6:391-415 |
| [43] | Hoogendoorn S P, Bovy P H L. Gas-kinetic modeling and simulation of pedestrian flows. Journal of the Transportation Research Board, 2007, 1710(1):28-36 |
| [44] | De Lillo S, Salvatori M C, Bellomo N. Mathematical tools of the kinetic theory of active particles with some reasoning on the modelling progression and heterogeneity. Mathematical and Computer Modelling, 2007, 45(5-6):564-578 |
| [45] | Bellomo N, Bellouquid A. On the modeling of crowd dynamics looking at the beautiful shapes of swarms. Networks and Heterogeneous Media, 2011, 6(3):383-399 |
| [46] | Delitala M. Nonlinear models of vehicular traffic flow-new frameworks of the mathematical kinetic theory. Comptes Rendus Mecanique, 2003, 331(12):817-822 |
| [47] | Arlotti L, De Angelis E, Fermo L, Lachowicz M, Bellomo N. On a class of integro-differential equations modeling complex systems with nonlinear interactions. Applied Mathematics Letters, 2012, 25(3):490-495 |
| [48] | Hilfer R. Applications of Fractional Calculus in Physics. New York:World Scientific Publishing Company, 2000. |
| [49] | Zaslavsky G M. Chaos, fractional kinetics, and anomalous transport. Physics Reports, 2002, 371(6):461-580 |
| [50] | Sokolov I M. Distributed-order fractional kinetics. Acta Physica Polonica B, 2004, 35(4):1323-1341 |
| [51] | Cao K C, Zeng C B, Stuart D, Chen Y Q. Fractional order dynamic modeling of crowd pedestrians. In:Proceedings of the 5th Symposium on Fractional Differentiation and Its Applications. Nanjing, China:Hohai University, 2012. |
| [52] | Wang L F, Yang X J, Baleanu D, Cattani C, Zhao Y. Fractal dynamical model of vehicular traffic flow within the local fractional conservation laws. Abstract and Applied Analysis, 2014, 35:1-5 |
| [53] | Bogdan P, Marculescu R. Towards a science of cyber-physical systems design. In:Proceedings of the 2011 IEEE/ACM International Conference on Cyber-Physical Systems. Chicago, IL:IEEE, 2011. 99-108 |
| [54] | Romanovas M, Klingbeil L, Trachtler1 M, Manoli Y. Fractional langevin models for human motion tracking in recursive Bayesian estimation algorithms. In:Proceedings of the 2009 Conference Mathematical Modelling and Analysis. Daugavpils, Latvia:MMA, 2009. 27-30 |
| [55] | Romanovas M, Traechtler M, Klingbeil L, Manoli Y. On fractional models for human motion tracking. Journal of Vibration and Control, 2013, 20(7):986-997 |
| [56] | Romanovas M, Klingbeil L, Traechtler M, Manoli Y. On fractional models for human motion tracking. In:Proceedings of the 5th Symposium on Fractional Differentiation and Its Applications. Nanjing, China:Hohai University, 2012. |
| [57] | Couzin I D, Krause J, James R, Ruxton G D, Franks N R. Collective memory and spatial sorting in animal groups. Journal of Theoretical Biology, 2002, 218(1):1-11 |
| [58] | Mogilner A, Edelstein-Keshet L, Bent L, Spiros A. Mutual interactions, potentials, and individual distance in a social aggregation. Journal of Mathematical Biology, 2003, 47(4):353-389 |
| [59] | John J, Tu Y H. Long-range order in a two-dimensional dynamical XY model:how birds fly together. Physical Review Letters, 1995, 75:4326-4329 |
| [60] | Zaslavsky G M, Edelman M, Tarasov V E. Dynamics of the chain of forced oscillators with long-range interaction:from synchronization to chaos. Chaos:An Interdisciplinary Journal of Nonlinear Science, 2007, 17(4):043124 |
| [61] | Hongler M O, Filliger R, Gallay O. Local versus nonlocal barycentric interactions in 1d agent dynamics. Mathematical Biosciences and Engineering, 2014, 11(2):303-315 |
| [62] | Ishiwata R, Sugiyama Y. Relationships between power-law long-range interactions and fractional mechanics. Physica A, 2012, 391(23):5827-5838 |
| [63] | Zhang H M. A mathematical theory of traffic hysteresis. Transportation Research Part B:Methodological, 1999, 33(1):1-23 |
| [64] | Tarasov V E, Zaslavsky G M. Fokker-Planck equation with fractional coordinate derivatives. Physica A:Statistical Mechanics and Its Applications, 2008, 387(26):6505-6512 |
| [65] | Colombo R M, Lécureux-Mercier M. Nonlocal crowd dynamics models for several populations. Acta Mathematica Scientia, 2012, 32(1):177-196 |
| [66] | Wadoo S A, Kachroo P. Feedback control design and stability analysis of one dimensional evacuation system. In:Proceedings of the 2006 Intelligent Transportation Systems Conference. Toronto, Ont.:IEEE, 2006. 618-623 |
| [67] | Wadoo S A, Kachroo P. Feedback control design and stability analysis of two dimensional evacuation system. In:Proceedings of the 2006 Intelligent Transportation Systems Conference. Toronto, Ont.:IEEE, 2006. 1108-1113 |
| [68] | Wadoo S A, Al-Nasur S, Kachroo P. Feedback control of macroscopic crowd dynamic models. In:Proceedings of the 2008 American Control Conference. Seattle, WA:IEEE, 2008. 2558-2563 |
| [69] | Wadoo S A, Kachroo P. Feedback control of crowd evacuation in one dimension. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1):182-193 |
| [70] | Dong H R, Yang X X, Chen Y, Wang Q L. Pedestrian evacuation in two-dimension via state feedback control. In:Proceedings of the 2013 American Control Conference. Washington, DC:IEEE, 2013. 302-306 |
| [71] | Shende A, Singh M P, Kachroo P. Optimization-based feedback control for pedestrian evacuation from an exit corridor. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4):1167-1176 |
| [72] | Shende A, Singh M P, Kachroo P. Optimal feedback flow rates for pedestrian evacuation in a network of corridors. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3):1053-1066 |
| [73] | Alvarez L, Roberto H, Perry L. Traffic flow control in automated highway systems. Control Engineering Practice, 1999, 7(9):1071-1078 |
| [74] | Yang X X, Dong H R, Chen Y, Wang Q L. Pedestrian evacuation in two-dimension via robust feedback control. In:Proceedings of the 10th IEEE International Conference on Control and Automation. Hangzhou, China:IEEE, 2013. 1087-1091 |
| [75] | Wadoo S A. Sliding mode control of crowd dynamics. IEEE Transactions on Control Systems Technology, 2013, 21(3):1008-1015 |
| [76] | Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 2003, 48(6):988-1001 |
| [77] | Dyer J R G, Johansson A, Helbing D, Couzin I D, Krause J. Leadership, consensus decision making and collective behaviour in humans. Philosophical Transactions of the Royal Society B, 2009, 364(1518):781-789 |
| [78] | Dyer J R G, Ioannou C C, Morrell L J, Croft D P, Couzin I D, Waters D A, Krause J. Consensus decision making in human crowds. Animal Behaviour, 2008, 75(2):461-470 |
| [79] | Aubé F, Shield R. Modeling the effect of leadership on crowd flow dynamics. In:Proceedings of the 6th International Conference on Cellular Automata for Research and Industry. Amsterdam, the Netherlands:Springer, 2004, 3305:601-611 |
| [80] | Kihong P, Walter W. Self-similar Network Traffic and Performance Evaluation. New York:John Wiley and Sons, Inc., 2000. |
| [81] | Marculescu R, Bogdan P. Cyberphysical systems workload modeling and design optimization. IEEE Design and Test of Computers, 2011, 28(4):78-87 |
| [82] | Li T, Zhang J F. Asymptotically optimal decentralized control for interacted ARX multi-agent systems. In:Proceedings of the 6th IEEE International Conference on Control and Automation. Guangzhou, China:IEEE, 2007. 1296-1301 |
| [83] | Huang M Y. Large-population LQG games involving a major player:the nash certainty equivalence principle. SIAM Journal on Control and Optimization, 2010, 48(5):3318-3353 |
| [84] | Cao Y G, Yu W W, Ren W, Chen G R. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Transactions on Industrial Informatics, 2013, 9(1):427-438 |
| [85] | Min H B, Liu Y, Wang S C, Sun F C. An overview on coordination control problem of multi-agent system. Acta Automatica Sinica, 2012, 38(10):1557-1570 |
| [86] | Nourian M, Malhame R P, Huang M, Caines P E. Mean field (NCE) formulation of estimation based leader-follower collective dynamics. International Journal of Robotics and Automation, 2011, 26(1):120-129 |
| [87] | Wang B C, Zhang J F. Distributed control of multi-agent systems with random parameters and a major agent. Automatica, 2012, 48(9):2093-2106 |
| [88] | Huang M Y, Caines P E, Malhame R P. Social optima in mean field LQG control:centralized and decentralized strategies. IEEE Transactions on Automatic Control, 2012, 57(7):1736-1751 |
| [89] | Nourian M, Caines P E, Malhame R P, Huang M Y. Nash, social and centralized solutions to consensus problems via mean field control theory. IEEE Transactions on Automatic Control, 2013, 58(3):639-653 |
| [90] | Nourian M, Caines P E, Malhame R P, Huang M Y. Mean field LQG control in leaderfollower stochastic multi-agent systems likelihood ratio based adaptation. IEEE Transactions on Automatic Control, 2012, 57(11):2801-2816 |
| [91] | Lasry J M, Lions P L. Mean field games. Japanese Journal of Mathematics, 2007, 2(1):229-260 |
| [92] | Dogbé C. Modeling crowd dynamics by the mean-field limit approach. Mathematical and Computer Modelling, 2010, 52(9-10):1506-1520 |
| [93] | Lachapelle A, Wolfram M T. On a mean field game approach modeling congestion and aversion in pedestrian crowds. Transportation Research Part B:Methodological, 2011, 45(10):1572-1589 |
| [94] | Helbing D, Molnár P. Social force model for pedestrian dynamics. Physical Review E, 1995, 51:4282-4286 |
| [95] | Liang J S, Chen Y Q. Diff-mas2-user's Manual. Technical Report, Center for Self-Organizing and Intelligent Systems (CSOIS), Department of Electrical and Computer Engineering, College of Engineering, Utah State University, USA, 2004. |
| [96] | He J P, Cheng P, Shi L, Chen J M. SATS:secure average-consensusbased time synchronization in wireless sensor networks. IEEE Transactions on Signal Processing, 2013, 61(24):6387-6400 |
| [97] | Liu H, Cao X H, He J P, Cheng P. Distributed identification of the most critical node for average consensus. In:Proceedings of the 19th International Federation of Automatic Control World Congress. Cape Town, South Africa:IFAC, 2014. 1843-1848 |
| [98] | Zhao C C, He J P, Cheng P, Chen J M. Secure consensus against message manipulation attacks in synchronous networks. In:Proceedings of the 19th International Federation of Automatic Control World Congress. Cape Town, South Africa:IFAC, 2014. 1182-1187 |
 2015, Vol.2
2015, Vol.2 


