ONE of the most important indicators for manufacturing industries is to precisely control various hardware such as servo motor and manufacturing system. Practically,the dynamics of a robot manipulator or servo motor are highly nonlinear,and because of loading effects or system failure,the system may always suffer from parameter or structure uncertainties. In fact,the control of nonlinear system with uncertainties is a tough task.
Iterative learning control (ILC) is considered to be the most powerful way to handle this problem effectively. According to the ILC theory,input signals will be refined based on the output error at every iteration,until the output tracks the desired trajectory for all the time interval. ILC shows uniform tracking performance and has been applied to wide areas[1],such as robotics,servo motors,batch reactors,aerodynamic systems and many new fields including agricultural industry[2],automatic train operation[3] and traffic control[4].
In 1984,Arimoto and his associates proposed the iterative learning control concept,and ILC was firstly adopted to improve the control performance of robots[5]. Since their pioneering work,ILC has been further explored and rapid progress has been achieved. Many ILC methods such as P-type,PD-type,PID-type, high-order,backward-forward learning laws and the concept of forgetting factor have been proposed[6]. Recent trend focuses on combining the above ILC methods with other control theories and algorithms,like adaptive control[7],neural network[8, 9],optimal control[10, 11],predictive control[12, 13],etc. And the design and analysis methods have been developed from contraction mapping theory to super vector approach[14],Lyapunov-like approach[15, 16, 17], frequency-domain method[18, 19] and 2-D based theory[20, 21]. Recent survey about ILC can be found in [22, 23, 24].
ILC is a powerful control strategy for nonlinear system with robust property,a good control property can be obtained even in the case that the precise model of the system is unknown. If the upper bound and Lipschitz condition of the parameters of the system can be satisfied,the system even with unmodeled dynamics can also be controlled to track the reference trajectory,and the stability and convergence property can be guaranteed[25, 26]. For system with unknown parameters,the unknown parameters can be identified in iteration axis by adaptive mechanism,and an adaptive ILC controller will be set up for the system with time variant parameters[27] or the nonlinear system with unknown parameters[28, 29, 30]. The adaptive ILC can be regarded as a kind of indirect adaptive control. It has been a new control method for nonlinear system,and the research in this field has attracted interest of more and more scholars in recent years.
In ILC method,the transient response improvement,that is,how to achieve satisfying control performance with least iteration times, is a noticeable problem. (It should be noted that the transient response in this paper refers to the least iteration times required for satisfactory tracking performance in iteration domain which is different from the transient response discussed in time domain for classical linear system.) In some circumstance,the iteration times may be too long to apply ILC effectively,especially when system failure occurs. The control performance may get worse due to long time spent in parameter identification when system parameter jumps drastically. On the other hand,according to the ILC theory for the unknown nonlinear dynamic systems,as long as the Lipschitz condition is satisfied,uniform tracking performance can be guaranteed even with partly known or estimated model. Though the exact model is not required,number of iterations for ILC with estimated model will increase compared with ILC with exact model.
One way to solve this problem is to introduce multiple model adaptive control (MMAC) to ILC. According to the MMAC theory, multiple models will be built based on the uncertainties of controlled model$'$s parameters and structure. Multiple controllers will be designed according to multiple element models. According to the given switching mechanism,the model with most appropriate elements to describe the plant will be decided,and the current controller will be switched to the controller corresponding to the best model. Multiple model adaptive control has been considered as one of the most effective control method for complex system for its ability to achieving high control accuracy,fast tracking speed and reliable stability[31]. Multiple model iterative learning control (MMILC) was introduced in [32]. In [32],before every iteration,the best model is decided by the multiple model adaptive control strategy and corresponding controller based on ILC learning law is activated,thus the transient response will be improved greatly. However,convergence is guaranteed in a strong condition that $\left\|\Psi_k\right\|<1$ (where $\Psi_k$ is defined below by (7)) which is not easy to be satisfied in most cases. Supposing that this condition cannot be established,[32] also provides a way to stop iteration at a final model where ${e_k} \leq \varepsilon $ ($e_k$ is the error between the actual and desired trajectory at the $k$th iteration and $\varepsilon $ is a given small positive number) or $k \geq {k_0}$ ($k$ is the iteration times and $k_0$ is the given finite positive integer). In this case,multiple model control is manually changed to be one model control which cannot get as perfect performance as ideal MMILC shows.
In this paper,for a class of nonlinear time-discrete system,we discuss the improvement and effectiveness of multiple model iterative learning control. A simplified control procedure is proposed,and the control output is proved to be convergent to the desired trajectory with relaxed conditions. The conditions $\left\|\Psi_k\right\|<1$,$e_k \leq \varepsilon$ and $k \geq k_0$ are no longer needed. Finally,simulation is given to show the effectiveness of the proposed method.
Ⅱ. ITERATIVE LEARNING CONTROL BASED ON MODEL ALGORITHMConsider the discrete-time unknown nonlinear system described as follows:
| \begin{align} {\pmb{x}}(t + 1) = {\pmb{f}}(\pmb{x}(t),t) + {\pmb{B}}(\pmb{x}(t),t){\pmb{u}}(t), \end{align} | (1) |
and the system is periodic in time $t$ with period $T$,i.e.,$t \in \{ 0,1,\cdots ,T\}$. The control vector and measurable state vector of the system are denoted by ${\pmb{u}}(t) {\in} {\bf{R}}^r$ and ${\pmb{x}}(t) {\in} {\bf{R}}^n$ respectively. Suppose that ${\pmb B}$ is full column rank and the system is full state output,the estimated model of $\{{\pmb f},{\pmb B}\}$ is known as $\{{\tilde {\pmb f}},{\tilde {\pmb B}}\}$,${\pmb B}$ and ${\tilde {\pmb B}}$ are bounded,${\tilde{\pmb f}}$ satisfies $\|{\tilde{\pmb f}}({\pmb x},t)\|\leq b_{\tilde {\pmb f}}\|{\pmb x}\|$,${\pmb f}$ and ${\pmb B}$ satisfy the uniformly global Lipschitz condition,i.e.,for arbitrary $t\in[0,T]$,${\pmb x}_1,{\pmb x}_2\in {\bf{R}}^n$,
$$\|{\pmb f}({\pmb x}_1,t)-{\pmb f}({\pmb x}_2,t)\|\leq k_{\pmb f}\|{\pmb x}_1-{\pmb x}_2\|,$$ $$\|{\pmb B}({\pmb x}_1,t)-{\pmb B}({\pmb x}_2,t)\|\leq k_{\pmb B}\|{\pmb x}_1-{\pmb x}_2\|,$$where $k_{\pmb f}$ and $k_{\pmb B}$ are Lipschitz constants.
To track the desired trajectory $\pmb{x}_d(t),t \in \{0,1,\cdots,T\}$,[25] proposed a ILC learning law based on partly known system model
| \begin{align} \pmb{u}_{k{+}1}(t)=\pmb{u}_{k}(t){+}\tilde{\pmb{B}}^{+}(\pmb{e}_k (t),t)[\pmb{e}_k (t{+}1){-}\tilde{\pmb{f}}(\pmb{e}_k(t),t)], \end{align} | (2) |
where
$${\pmb{e}}_k(t)={\pmb{x}}_d(t)-{\pmb{x}}_k(t),$$ $${\tilde{\pmb{B}}^ + }({{\pmb{e}}_k}(t),t) = {[{\tilde{\pmb{B}}^{\rm T}} ({{\pmb{e}}_k}(t),t){\tilde{\pmb{B}}}({{\pmb{e}_k}}(t),t)]^{ - 1}}{\tilde{\pmb{B}}^{\rm T}}({{\pmb{e}}_k}(t),t),$$and ${k}$ indicates the iteration times.
For system (1),suppose that the imposed initial control input $\pmb{u}_0(t)$ is continuous and selected arbitrarily,when learning law (2) is applied,uniform convergence can be guaranteed by the following lemma.
Lemma 1[25]. For accessible desired trajectory ${{\pmb{x}}_d}(t)$ $(0 \leq t \leq T)$,if system $(1)$ satisfies the following conditions:
a) $\left\| {{{I}} - {{{\tilde{\pmb{B}}}}^ + }({\pmb{e}}(t),t){\pmb{B}}(\pmb{x}(t),t)} \right\| < 1 (0 \leq t \leq T);$
b) ${{\pmb{x}}_k}(0) = {{\pmb{x}}_d}(0).$
Then by the effect of learning algorithm (2),as $k \to \infty$, $\left\| {{{\pmb{e}}_k}(t)} \right\| {\to} 0\ (0 \leq t \leq T)$.
The proof of Lemma 1 is in Appendix A.
Ⅲ. ILC BASED ON MULTIPLE MODELSIn practical control process for systems that perform the same task iteratively,there are lots of environments where parameters are unknown or uncertain. Although ILC method can handle this problem effectively,ILC based on multiple models can give a more perfect performance. In this section,we discuss the establishment of model set and corresponding controllers,the selection of switching performance index function,and the procedure of the improved multiple model ILC.
For a time-varying system,the plant$'$s parameters change either slowly or abruptly. In this section,a special case is considered, where the plant$'$s parameters are constant first and then jump abruptly to another constant value. For system (1), ${\pmb{f}}({\pmb{x}}(t),t)$ and ${\pmb{B}}({\pmb{x}}(t),t)$ can be described by ${\pmb{f}}({\pmb{x}}(t),\theta (t),t)$ and ${\pmb{B}}({\pmb{x}}(t),\alpha (t),t)$,where $\theta (t)$ and $\alpha (t)$ are piece-wise constant vectors in time $t$. In the case of ILC,system (1) can be rewritten as
| \begin{align} {\pmb{x}_k}(t + 1) = {\pmb{f}}(\pmb{x}_k(t),\theta _k(t),t) + {\pmb{B}}(\pmb{x}_k(t),\alpha_k (t),t){\pmb{u}}_k(t), \end{align} | (3) |
where $t\in\{1,2,\cdots,T\}$; $k=0,1,\cdots,\infty$; $\left( {\theta _k(t),\alpha _k(t)} \right) \in \left\{ \left( {\theta _{{j_1}},\alpha _{{j_2}}} \right)|j_1=1,2,\cdots,d_{\theta}; j_2=1,2,\cdots,d_{\alpha}\right\}$. And $d_\theta$,$d_\alpha$ are finite integers known a priori.
For notational simplicity,we denote $\pmb{f}(\pmb{x}(t))$ = $\pmb{f}(\pmb{x}(t),t)$,$\pmb{f}(\pmb{x}(t),\theta (t))$ = $\pmb{f}(\pmb{x}(t),\theta (t),t)$, and the same notation method is applied to matrix functions related to $\pmb{B}$.
A. Model Set and Corresponding ControllersIn general,traditional adaptive control is efficient when the model parameter is constant or varies slowly. In practice,for complex system which may change from one operating environment to another abruptly,parameter may also change dramatically in a short time,resulting in model inaccuracy. And it has been found that conventional adaptive control method shows poor performance for complex system.
According to the MMAC theory,to cover the uncertainty of system, multiple models responding to different environments are built. And for every environment,there must be at least one model which is close enough to the current unknown plant. When one model is considered to be the most accurate one to describe the plant, corresponding controller will be selected to control the plant. The model can be either fixed or adaptive. In this paper,we consider the simplest case that all models are fixed. Based on the estimated values ${\tilde{\theta}_{i_1}}(i_1=1,2,\cdots,d_1)$ and ${\tilde{\alpha}_{i_2}}(i_2=1,2,\cdots,d_2)$ of parameters ${ {\theta}}$ and $\alpha$ respectively,model set can be set up as
$$M{=}\left\{M_i{=}\left\{\tilde {\pmb{f}}(\pmb{x}(t),\tilde{\theta}_{i_1}), \tilde {\pmb{B}}(\pmb{x}(t),\tilde{\alpha}_{i_2})|i=(i_1,i_2)\in \Pi\right\}\right\},$$where $\Pi {=}\left \{(i_1,i_2)| i_1{=}1,2,\cdots,d_1;i_2{=}1,2,\cdots,d_2\right \}$.
For notional simplicity,let $\tilde {\pmb{f}}_{i_1}(\pmb{x}(t))=\tilde {\pmb{f}}(\pmb{x}(t),\tilde{\theta}_{i_1},t)$ and $\tilde {\pmb{B}}_{i_2}(\pmb{x}(t))=\tilde {\pmb{B}}(\pmb{x}(t),\tilde{\alpha}_{i_2},t)$. Suppose that ${\tilde {\pmb B}}_{i_2}\ (i_2=1,2,\cdots,d_2)$ are bounded, $\|{I} - {{\tilde{\pmb B}}^ +_{i_2} }({{\pmb{e}}_k}(t)){\pmb{B}}_{i_2}({{\pmb{x}}_k}(t))\|<1$,and $\forall i_1=1,2,\cdots,d_1$,${\tilde {\pmb f}}_{i_1}$ satisfies $\|{\tilde {\pmb f}}_{i_1}({\pmb x},t)\|\leq b_{{\tilde {\pmb f}}_{i_1}}\|{\pmb x}\|$.
For unknown nonlinear dynamic system,ILC will be formed based on partly known or estimated model,and the exact knowledge of system will not be required. However,the more precise the model is,the faster transient response we may get. An index function will be calculated to decide which model describes the plant best.
According to the model set we just established,corresponding controllers will be formed based on the ILC control strategy (2).
| \begin{align} C=\left \{ C_i|i\in \Pi\right\}, \end{align} | (4) |
where
\begin{equation*} %\begin{split} {C_i}{:} {{\pmb{u}}_{k {+} 1}}(t) ={{\pmb{u}}_k}(t){+} {{{\tilde {\pmb B}}}^+_{i_2} }({{\pmb{e}}_k}(t))\Big[{{\pmb{e}}_k}(t {+} 1){-}{\tilde {\pmb f}}_{i_1}({{\pmb{e}}_k}(t)) \Big], %\end{split} \end{equation*} $${\pmb{e}}_k(t)={\pmb{x}}_d(t)-{\pmb{x}}_k(t),$$ $${\tilde{\pmb{B}}_{i_2}^ + }({{\pmb{e}}_k}(t)) = {[{\tilde{\pmb{B}}^{\rm T}_{i_2}}({{\pmb{e}}_k}(t)){\tilde{\pmb{B}}_{i_2}} ({{\pmb{e}_k}}(t))]^{ - 1}}{\tilde{\pmb{B}}^{\rm T}_{i_2}}({{\pmb{e}}_k}(t)).$$The index function will decide the best model,and corresponding controller will be selected to control the system,thus,the performance of transient response may be improved.
B. Switching Performance IndexThe switching mechanism is proposed to decide the most accurate model for current environment at every iteration and activate the corresponding controller. A typical switching mechanism is based on the performance index function $L_{i,k}(t)$ for each model $M_i$ at the $k$th iteration. The index function should consider the long-term error accumulation to estimate the elemental model accuracy reliably. The following index switching function is given:
$$L_{i,k}=\sum\limits_{m=1}^T \beta^{T-m} e_k^i(m),\quad 0<\beta\leq 1,$$where
$${\pmb{x}}_k(t + 1) = {\pmb{f}}({\pmb{x}_k}(t),\theta_k(t)) + {\pmb{B}}({\pmb{x}_k}(t),\alpha _k(t)){{\pmb{u}}_k}(t),$$ $${\tilde{\pmb{x}}_k^i}(t + 1) = \tilde{\pmb{f}}_{i_1}({\pmb{x}_k (t)}) + \tilde{\pmb{B}}_{i_2}({\pmb{x}_k (t)}){{\pmb{u}}_k}(t),$$ $$e_k^i(t) = {\left\| {{{\pmb{x}}_k}(t + 1) - {{{\tilde{\pmb{x}}}}_k^i}(t + 1)} \right\|^2},$$${\tilde{\pmb{x}}_k^i(t+1)}$ denotes the state output of model $M_i$ at the $k$-th iteration by the use of the known $\pmb{u}_k(t)$ and the measurable $\pmb{x}_k(t)$.
For iteration with parameter jumping,errors between model and system before the jumping point are less important than those after this point to calculate the model performance index. And the forgetting factor $\beta$ determines the rate at which each model$'$s past estimation errors are attenuated. According to ILC theory,control signals will be refined through iteration until the desired input is achieved. Before every iteration,switching index of every elemental model $L_{i,k}(i\in \Pi)$ is calculated, the model with the smallest error will be selected,i.e.,model $l(k)$ is selected if $l(k)=_{i\in \Pi} L_{i,k}$.
C. Improved Multiple Model ILCAssuming that the parameters $\theta$ and $\alpha$ of ${\pmb{f}}({\pmb{x}}(t),\theta(t))$ and ${\pmb{B}}({\pmb{x}}(t),\alpha(t))$ vary in convex sets $\Omega_\theta$ and $\Omega_\alpha$ respectively,and the upper bounds of $k_p^i$ and $\left\| { _k^i(t)}\right\|$ exist,where $k_p^i$ and $\left\| { _k^i(t)} \right\|$ will be given in Theorem 1. The following improved multiple model ILC can be given as below:
1) Multiple model set of ${\pmb{f}}({\pmb{x}}(t),\theta(t))$ and ${\pmb{B}}({\pmb{x}}(t),\alpha(t))$ will be set up as below:
| \begin{align} M{=}\left\{M_i{=}\{\tilde {\pmb{f}}_{i_1}(\pmb{x}(t)),\tilde {\pmb{B}}_{i_2}(\pmb{x}(t))\}|i=(i_1,i_2)\in\Pi\right\}. \end{align} | (5) |
2) At the end of the $k$th iteration,the best model to describe the current environment will be selected,i.e.,
| \begin{align} l(k) = {\mathop{\arg}\min\limits_{i \in \Pi }} \sum\limits_{m = 1}^T {{\beta ^{T - m}}e_k^i(m)}. \end{align} | (6) |
Denote $l(k)=(l_1(k),l_2(k))$. It will switch to controller $C_{l(k)}$ based on model $M_{l(k)}=\left\{{\tilde{\pmb{f}}}_{l_1(k)}({\pmb{x}}(t)),{\tilde{\pmb{B}}}_{l_2(k)}({\pmb{x}}(t))\right\}$ in the next iteration.
Ⅳ. THE STABILITY OF THE IMPROVED MMILCOne of the most significant characteristics of a successful MMAC design is that the stability of the closed system can be guaranteed even with infinite switching times among multiple models.
In [32],the switching times of multiple controller is considered in the following two ways:
Case 1. Finite switching times
In this case,an upper bound $\varepsilon $ of trajectory error,and a lower bound ${k_0}$ of iteration times should be given,then the switching will be ceased if
$$\sum\limits_{m = 1}^T {\parallel {x_k}(m) - {x_d}(m){\parallel ^2} \le \varepsilon {\kern 1pt} {\kern 1pt} } or{\kern 1pt} {\kern 1pt} k \ge {k_0}.$$The switching is stopped in finite switching times.
Case 2. Infinite switching times
In this case,a condition $\left\| {{\Psi _k}} \right\| < 1$ should be satisfied. Thus,even with infinite switching,the performance of uniform tracking can be guaranteed.
| \begin{align} {\Psi _k}= \begin{bmatrix} \left\| {{_{k }}(0)} \right\|&0&\cdots&0\\ K_0&\left\| {{_{k }}(1)} \right\|&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ K_0&K_1&\cdots&\left\| {_{k }}(T) \right\| \end{bmatrix}, \end{align} | (7) |
where ${ _k}(t) = {I} - {{\tilde{\pmb B}}^ + }({{\pmb{e}}_k}(t),t){\pmb{B}}({{\pmb{x}}_k}(t),t)$ and
$$K_p=k_t k_{2,t-1}\cdots k_{2,p+1}k_{1,p}~~(p=0,1,2,\cdots,t-1),$$where $k_t=\|{\tilde {\pmb{B}}}^+(e_k(t),t)\|(k_{\pmb B}\|{\pmb u}_d(t)\|+k_{\pmb f}+b_{\tilde {\pmb {f}}})$,$k_{1,t}=\|{\pmb B}({\pmb x}_k(t),t)\|$,$k_{2,t}=k_{\pmb f}+k_{\pmb B}\|{\pmb u}_d(t)\|$. As $k_t$ and $k_{1,t}$ are both related to $k$ and $t$,$K_p$ is relevant to $k$ and $t$.
In Case 1,the switching will be stopped at one final model. Thus,multiple model ILC is finally changed into a conventional ILC based on a single model. Though the stability can be got as traditional ILC method,the result is not the best one. The ideal result is that even with infinite times of iteration,the control stability can be guaranteed.
Though infinite switching stability can be guaranteed in Case 2, a really strong condition that $\left\| {{\Psi _{{k}}}} \right\| < 1$ must be satisfied. From (7),we can see that ${{{\Psi}}_k}$ is a lower triangular matrix whose all nonzero elements are related to both $k$ and $t$. With the increment of $k$ and $t$,the condition is hard to be satisfied because the nonzero elements of ${{{\Psi }}_k}$ may be relatively big. Thus,infinite switching stability is not easy to be guaranteed.
The infinite switching condition in [32] is so strict that it can be satisfied only in rare circumstances,which limits the application scope of multiple model ILC. In this paper,we will relax this condition,and it can be proved that infinite switching stability can be guaranteed without the constraint of $\left\| {{\Psi _{\rm{k}}}} \right\| < 1$.
Lemma 2. For $A\in {{\bf C}}^{n\times n}$ with its eigenvalues $\lambda_i,i\in \{1,2,\cdots,n\}$,if $\max_{i\in \{1,2,\cdots, n\}}{|\lambda_i|}<\delta<1$,the following inequality can be guaranteed:
$$\|A^k\|_2<\sigma \gamma^k,$$where $\sigma$ is a positive constant and $\delta<\gamma<1$.
The proof of Lemma 2[33, 34] is in Appendix B.
Theorem 1. For system $(3)$,for every elemental model $M_i$,if the following conditions are satisfied:
a) The upper bound of $K_p^i$ exists,i.e.,
$$K_p^u=\mathop{\ \sup\ }_{i\in \Pi}K_p^i.$$b) The upper bound of $\left\| { _k^i(t)} \right\|$ exists and satisfies
$${\rho^u(t)}=\mathop{\ \sup\ }_{i\in \Pi}\left\| { _k^i(t)} \right\|<1.$$c) ${{\pmb{x}}_k}(0) = {{\pmb{x}}_d}(0)$,
where \begin{align*} &{_k^i}(t) = {I} - {{\tilde{\pmb B}}_{i_2}^ + }({{\pmb{e}}_k}(t),t){\pmb{B}}({{\pmb{x}}_k}(t),t),\\ &K_p^i=k_t^i k_{2,t-1}\cdots k_{2,p+1}k_{1,p},\\ &p=0,1,2,\cdots,t-1,\\ &k_t^i=\|{\tilde {\pmb{B}}}_{i_2}^+({\rm e}_k(t),t)\|(k_{\pmb B}\|{\pmb u}_d(t)\|+k_{\pmb f}+b_{{\tilde {\pmb {f}}}_{i_1}}),\\ & \Pi =\left \{(i_1,i_2)| i_1{=}1,2,\cdots,d_1;i_2{=}1,2,\cdots,d_2\right \}, \end{align*}then even with infinite switching times,the state of the system will track the desired trajectory asymptotically.
Proof. For single model ILC,from the proof of Lemma 1 given in Appendix A,we can get
| \begin{align} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{bmatrix} \leq {\Psi _k} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k }}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k }}(T)} \right\| \end{bmatrix}. \end{align} | (8) |
For system (3),when control algorithm (2) is applied,multiple models are given by $M_i{=}\left\{\tilde {\pmb{f}}_{i_1}(\pmb{x}(t)),\tilde {\pmb{B}}_{i_2}(\pmb{x}(t))\right\}$. Since ${_k}(t)$,${K_p}$ and ${\Psi_k}$ are all relative to $\{{\tilde{\pmb f}},{\tilde{\pmb B}}\}$,for notational simplicity,we define $_k^{i}(t)$,$K_p^{i}$ and $\Psi_k^{i}$ as the ${_k}(t)$, ${K_p}$ and ${\Psi _k}$ corresponding to model $M_{i}$.
Considering in the $(k+1)$-th iteration,model $M_{l(k)}$ is used. So in the structure of MMILC,we have
| \begin{align} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{bmatrix} \leq {\Psi _k^{l(k)}} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k }}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k }}(T)} \right\| \end{bmatrix}, \end{align} | (9) |
where
| \begin{align} \Psi _k^{l(k)}= \begin{bmatrix} \left\| {{_{k }^{l(k)}}(0)} \right\|&0&\cdots&0\\ K_0^{l(k)}&\left\| {{_{k }^{l(k)}}(1)} \right\|&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ K_0^{l(k)}&K_1^{l(k)}&\cdots&\left\| {_{k }^{l(k)}}(T) \right\| \end{bmatrix} , \end{align} | (10) |
where $\left\| {{_{k }^{l(k)}}(0)} \right\|,\cdots,\left\| {{_{k }^{l(k)}}(T)} \right\|$,$K_0^{l(k)},\cdots,K_T^{l(k)}$ are the coefficients corresponding to model $l(k)$. From (8) $\sim$ (10),we have
| \begin{align} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{bmatrix} \leq {\Psi _k^{l(k)}}{\Psi _{k-1}^{l(k-1)}}\cdots{\Psi _{0}^{l(0)}} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{0 }}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{0 }}(T)} \right\| \end{bmatrix} . \end{align} | (11) |
Considering $0 \leq K_p^{l(k)} \leq K_p^u (p = 0,\cdots ,T - 1)$,$0 \leq \left\| {{_{k }^{l(k)}}(t)} \right\| \leq \rho ^u(t)<1$,and $\left\| {\Delta {{\pmb{u}}_{k }}(t)} \right\|\geq0 (t=0,\cdots,T)$,we have
| \begin{align} \begin{bmatrix} \begin{smallmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{smallmatrix} \end{bmatrix} {\leq} {\begin{bmatrix} \begin{smallmatrix} {\rho^{u}(0)} &0&\cdots&0\\ K_0^{u}& {{\rho^{u}}(1)} &\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ K_0^{u}&K_1^{u}&\cdots& {\rho^{u}}(T) \end{smallmatrix} \end{bmatrix}^{k+1}} \! \begin{bmatrix} \begin{smallmatrix} \left\| {\Delta {{\pmb{u}}_{0}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{0}}(T)} \right\| \end{smallmatrix} \end{bmatrix} , \end{align} | (12) |
if we denote
| \begin{align} \Psi^u= \begin{bmatrix} {\rho^{u}(0)} &0&\cdots&0\\ K_0^{u}& {{\rho^{u}}(1)} &\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ K_0^{u}&K_1^{u}&\cdots& {{\rho}^{u}}(T) \end{bmatrix}, \end{align} | (13) |
| \begin{align} \left[ {\begin{array}{*{20}{c}} {\left\| {\Delta {\rm{\backslash pmb}}{u_{k + 1}}(0)} \right\|}\\ \vdots \\ {\left\| {\Delta {\rm{\backslash pmb}}{u_{k + 1}}(T)} \right\|} \end{array}} \right] \le {({\Psi ^u})^{k + 1}}\left[ {\begin{array}{*{20}{c}} {\left\| {\Delta {\rm{\backslash pmb}}{u_0}(0)} \right\|}\\ \vdots \\ {\left\| {\Delta {\rm{\backslash pmb}}{u_0}(T)} \right\|} \end{array}} \right]. \end{align} | (14) |
Because $\Psi^u$ is a lower triangular matrix,and its diagonal elements ${\rho}^u(t)<1 (t=0,1,\cdots,T)$,according to Lemma 2, we have
$$\left\|(\Psi^u)^{k+1} \right\|_2\leq \sigma\gamma^{k+1},$$where $\sigma$ is a positive constant and $0<\gamma<1$.
Furthermore,we have
| \begin{align} \left\| \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{bmatrix} \right\|_2 \leq \sigma\gamma^{k+1} \left\| \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k }}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k }}(T)} \right\| \end{bmatrix} \right\|_2. \end{align} | (15) |
As $\sigma$ is constant and $0<\sigma<\infty$, $0<\gamma<1$,so when $k \to \infty$,we have
| \begin{align} \left\| \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{bmatrix} \right\|_2 \to 0, \end{align} | (16) |
further,
$$\left\| {\Delta {{\pmb{u}}_k}} \right\| \to 0.$$and from (A3) of Appendix A and condition c) of Theorem 1, we have ${{\pmb{x}}_k}(t) \to {{\pmb{x}}_d}(t)$,as $k \to \infty $.
Remark 1. Consider the definition of $K_p^i$ under the assumptions that ${\pmb f}$ and ${\pmb B}$ satisfy the uniform Lipschitz condition,${\pmb B}$ and ${{\tilde{\pmb{B}}}}_{i_2}$ are bounded and $\|{{\tilde{\pmb{f}}}}_{i_1}({\pmb{x}})\|\leq b_{{\tilde{\pmb{f}}}_{i_1}}\|{\pmb{x}}\|$,condition a) of Theorem 1 can be guaranteed.
Remark 2. As the established models satisfy $\|{I} - {{\tilde{\pmb B}}_{i_2}^ + }({{\pmb{e}}_k}(t),t){\pmb{B}}({{\pmb{x}}_k}(t),t)\|<1$,condition b) of Theorem 1 can be guaranteed.
Through the above analysis,we can see that the proposed improved MMILC method only requires the established multiple models satisfy assumptions which traditional single model ILC must be satisfied. And the stability can be guaranteed even with infinite switching times.
Ⅴ. SIMULATIONConsider a discrete-time unknown nonlinear system in form
\[\left[\begin{array}{l} {x_1}(t + 1)\\ {x_2}(t + 1) \end{array} \right] = \left[\begin{array}{c} x_2(t)\\ \dfrac{{{x_1}(t){x_2}(t)\left( {{x_2}(t) + v(t)} \right)}}{{1 + x_1^2(t) + x_2^2(t)}} \end{array} \right] + \left[\begin{array}{l} 0\\ 1 \end{array} \right]u(t),\]the desired state trajectory $\pmb x_d(t)$ is given by
\begin{equation*} \pmb x_d(t)= \begin{bmatrix} {x_{1d}}(t)\\ {x_{2d}}(t) \end{bmatrix}= \begin{bmatrix} \dfrac{\pi\times 10^{-3}}{12}\sin \left(\dfrac{{\pi t}}{{80}}\right)\\ \dfrac{\pi\times 10^{-3}}{12}\sin \left( {\dfrac{{\pi (t + 1)}}{{80}}} \right) \end{bmatrix}. \end{equation*}Compared with system (3),the $\pmb{f}$ part of the controlled system satisfies the Lipschitz condition apparently,and the corresponding $\pmb{B}$ part is a constant matrix which is also bounded,so the upper bounds of $k_p^i$ and $\left\|{\boldsymbol \rho}_k^i(t)\right\|$ both exist. We conducted simulations for two cases: one for the system with constant parameter,and the other for system with jumping parameter.
Case 1. ILC for system with constant parameter
When $v(t)\equiv 1$,the estimated value of $v(t)$ is $\tilde{v}=2$,corresponding ILC model is shown as
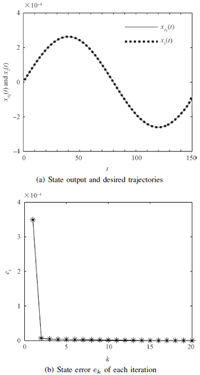
$$\tilde{\pmb{f}} (\pmb{x}(t),t)= \left[\begin{array}{c} x_2(t)\\ \dfrac{{{x_1}(t){x_2}(t)\left( {{x_2}(t) + \tilde{v}} \right)}}{{1 + x_1^2(t) + x_2^2(t)}} \end{array} \right].$$Fig. 1 depicts the state and desired trajectories and the curve of output error $e_k$ given as below:
$$ e_k=\left\|{{{\pmb{x}}_k}(i) - {{\pmb{x}}_d}(i)} \right\|^2$$and we can see that after about 15 trials,the output error converges to zero.
|
Download:
|
| Fig. 1.Parameter-fixed system using conventional ILC. | |
Case 2. System with jumping parameter
When parameter $v$ is piecewise constant depicted by
$$v(k,t) = \left\{ \begin{array}{l l} 1,&\quad \ k<4,\quad t \in (1,2,\cdots,150)\\ 9,&\quad \ k=4,\quad t \in (1,2,\cdots,100)\\ 6,&\left\{ \begin{array}{l l} k=4,&~t \in (101,102,\cdots,150)\\ k>4,&~t \in (1,2,\cdots,150) \end{array} \right. \end{array} \right.$$where $k$ represents the iteration times. In practice, $v(k,t)$ is the parameter which is measured imprecisely,or estimated by experienced workers. In our simulation,the estimation of $v(k,t)$ is selected randomly around the true value. Numerous experiments show that other estimation of $v(k,t)$ can also get similar results. Four estimated values of $v(k,t)$ are given as $\tilde{v}_1=2,\tilde{v}_2=10,\tilde{v}_3=6.5,\tilde{v}_4=5.5$. For system with jumping parameter,we consider two cases by using single model ILC and multiple model ILC.
1) A single model ILC
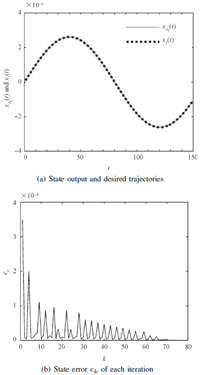
$$\tilde{\pmb{f}} (\pmb{x}(t),t)= \left[\begin{array}{c} x_2(t)\\ \dfrac{{{x_1}(t){x_2}(t)\left( {{x_2}(t) + \tilde{v}_1} \right)}}{{1 + x_1^2(t) + x_2^2(t)}} \end{array} \right].$$When single model ILC is applied to the system with jumping parameter,about 75 iteration times are needed for the state to converge to the desired trajectory as shown in Fig. 2.
|
Download:
|
| Fig. 2. Parameter-jumping system using conventional ILC. | |
2) Multiple model ILC
$$\tilde{\pmb{f}_i} (\pmb{x}(t),t)= \left[\begin{array}{c} x_2(t)\\ \dfrac{{{x_1}(t){x_2}(t)\left( {{x_2}(t) + \tilde{v}_i} \right)}}{{1 + x_1^2(t) + x_2^2(t)}} \end{array} \right],$$where ${{\tilde {\pmb f}}_i}({\pmb{x}}(t),t)$,$i \in \left\{ {1,2,3,4} \right\}$ represents four estimated models corresponding to $\tilde {v}_1$,$\tilde {v}_2$,$\tilde {v}_3$ and $\tilde {v}_4$.
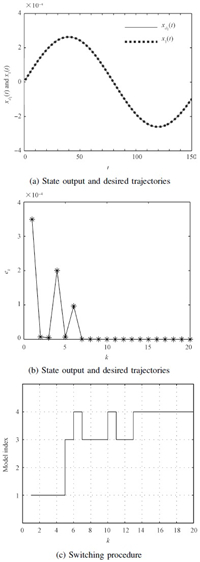
The control result is shown in Fig. 3,and Fig. 3(c) depicts the switching procedure that how the best model is selected at every iteration. Parameter $\beta$ of switching index function is set to be 0.9.
|
Download:
|
| Fig. 3. Parameter-jumping system using multiple model ILC. | |
From Fig. 1,we can see that for nonlinear system with fixed parameter,the uniform convergent performance can be reached after about 15 iterations when conventional ILC method is applied. When the same control method is applied to system with jumping parameter, as shown in Fig. 2,the state error decreases sharply at the first 3 trials the same as for the system with fixed parameter shown in Fig. 1 (b). However,when parameter changes at the 4th and 5th trial,corresponding error increases sharply in the next trial,that is because the estimated model is no longer compatible with the system,numerous times of iterative learning (about 75) is needed for conventional ILC based on single model is no longer applicable.
But for multiple model ILC shown in Fig. 3,the four models contain all possible situations and the best model will be decided after every iteration. So it can be seen clearly in Fig. 3 (c) that the most precise model is selected after parameter $v$ changes. When $k=4$,$v$ changes from 1 to 9,and at the end of the 4th trial, model 2 is calculated to be the most precise one instead of model 1, so model 2 is selected when the 5th trial begins. Based on this kind of control strategy,as shown in Fig. 3 (b),after about 10 trials the state output error approaches zero,while 75 trials are needed for a single model ILC shown in Fig. 2 (b). In Fig. 3 (c) it can be seen that after about 14 iterations,MMILC stops switching and it stabilizes at the 4th model.
The simulations show that iteration times can be decreased apparently based on multiple model method compared with conventional ILC strategy. So we can easily come to the conclusion that for a complex nonlinear system,multiple model iterative learning control can significantly improve the performance of transient response.
Ⅵ. CONCLUSIONFor complex nonlinear system with uncertainty,it is a good method to combine ILC with multiple model adaptive control which can cover the uncertainty and select the best model for every current circumstance. However,former MMILC method needs the switching to be ceased manually,or a very strict condition was needed to be satisfied. In this paper,an improved multiple model ILC method is proposed. First,a class of system to be handled is described,ILC method based on model algorithm is presented and is proved to be effective to track the desired trajectory uniformly. Then,a simplified MMILC procedure is presented,without extra stopping condition,the state output error converges to zero asymptotically even with infinite switching times. In particular,the improved multiple model ILC is proved to be convergent with a relaxed condition which expands the application scope greatly. Finally,the simulations show that the improved multiple model ILC can improve the performance of transient response greatly compared with conventional iterative learning control.
APPENDIX A PROOF OF LEMMA 1[25]Proof. From (2),we can get
\begin{align} \begin{array}{*{20}{l}} {\Delta {u_{k + 1}}(t) = \Delta {u_k}(t) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\tilde B}^ + }({e_k}(t))\left[ {{e_k}(t + 1) - \tilde f({e_k}(t))} \right].} \end{array} \end{align}Since
| \begin{align} \begin{array}{*{20}{l}} {{e_k}(t + 1) = }&{B({x_k}(t))\Delta {{\rm{u}}_k}(t) + f({x_d}(t)) - f({x_k}(t)) + }\\ {}&{\left[ {B({x_d}(t)) - B({x_k}(t))} \right]{u_d}(t){\rm{ }},} \end{array} \end{align} | (A1) |
then
| \begin{align} \begin{array}{l} \Delta {u_k}(t + 1) = \Delta {u_k}(t) - {{\tilde B}^ + }({x_k}(t))\Delta {u_k}(t) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\tilde B}^ + }({e_k}(t))[B({x_d}(t)) - B({x_k}(t))]{u_d}(t) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\tilde B}^ + }({e_k}(t))[f({x_d}(t)) - f({x_k}(t))] - \tilde f({e_k}(t))] \end{array} \end{align} | (A2) |
Taking norms of both sides of (A1) gives
| \begin{align} \begin{array}{l} \parallel {e_k}(t + 1)\parallel \le \parallel {\rm{B}}({x_k}(t))\parallel \parallel \Delta {u_k}(t)\parallel + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_f}\parallel {x_d}(t) - {x_k}(t)\parallel + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_B}\parallel {x_d}(t) - {x_k}(t)\parallel \parallel {u_d}(t)\parallel = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_{1,t}}\parallel \Delta {u_k}(t)\parallel + {k_{2,t}}\parallel {e_k}(t)\parallel , \end{array} \end{align} | (A3) |
where ${k_{1,t}}\parallel {\rm{B}}({x_k}(t))\parallel ,{k_{2,t}} = {k_f} + {\kern 1pt} {k_B}\parallel {u_d}(t)\parallel ,$,and $k_{2,t}$ is irrelevant to $k$.
Taking norms of both sides of (A2) gives
| \begin{align} \begin{array}{l} \parallel \Delta {u_{k + 1}}(t)\parallel \le {\rho _k}(t)\parallel \parallel \Delta {u_k}(t)\parallel + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \parallel {{{\rm{\tilde B}}}^ + }({{\rm{e}}_k}(t))\parallel {\kern 1pt} {\kern 1pt} {k_B}\parallel {{\rm{e}}_k}(t)\parallel \parallel {u_d}(t) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_f}\parallel {{\rm{e}}_k}(t) + {b_{\tilde f}}\parallel {{\rm{e}}_k}(t)\parallel {\kern 1pt} {\kern 1pt} ) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \parallel {\rho _k}(t)\parallel \parallel \Delta {u_k}(t)\parallel + {k_t}\parallel {{\rm{e}}_k}(t)\parallel , \end{array} \end{align} | (A4) |
where ${k_t} = {{{\rm{\tilde B}}}^ + }({{\rm{e}}_k}(t))\parallel {\kern 1pt} {k_B}\parallel {u_d}(t)\parallel + {k_f} + {b_{\tilde f}}$ and ${\rho _k}(t) = I - {{{\rm{\tilde B}}}^ + }({{\rm{e}}_k}(t)){\rm{B}}({x_k}(t))$ are both relevant to $k$. Considering (A3) and (A4),we have
| \begin{align} \begin{array}{l} \parallel \Delta {u_{k + 1}}(t)\parallel \le {\rho _k}(t)\parallel \parallel \Delta {u_k}(t)\parallel + {k_t}({k_{1,t - 1}}\parallel \Delta {u_k}(t - 1)\parallel + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_{2,t - 2}}\parallel {{\rm{e}}_k}(t - 1)\parallel {\kern 1pt} {\kern 1pt} ) \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \parallel {\rho _k}(t)\parallel \parallel \Delta {u_k}(t)\parallel + {K_{t - 1}}\Delta {u_k}(t - 1)\parallel + \cdots + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_0}\parallel \Delta {u_k}(0)\parallel , \end{array} \end{align} | (A5) |
where $K_p=k_tk_{2,t-1}\cdots k_{2,p+1}k_{1,p}~ (p=0,1,2,\cdots,t-1)$. Rewrite (A5) from $t=0$ to $t=T$
\begin{align*} \begin{array}{l} \parallel \Delta {u_{k + 1}}(0)\parallel \le {\kern 1pt} {\kern 1pt} \parallel {\rho _k}(0)\parallel \parallel \Delta {u_k}(0)\parallel ,\\ \parallel \Delta {u_{k + 1}}(1)\parallel \le {\kern 1pt} {\kern 1pt} \parallel {\rho _k}(1)\parallel \parallel \Delta {u_k}(1)\parallel + {K_0}\parallel \Delta {u_k}(0)\parallel , \end{array} \end{align*}Rewriting the above into the form of matrix,we have
| \begin{align} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k + 1}}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k + 1}}(T)} \right\| \end{bmatrix} \leq {\Psi _k} \begin{bmatrix} \left\| {\Delta {{\pmb{u}}_{k }}(0)} \right\|\\ \vdots\\ \left\| {\Delta {{\pmb{u}}_{k }}(T)} \right\| \end{bmatrix}, \end{align} | (A6) |
where
| \begin{align} {\Psi _k} = \left[ {\begin{array}{*{20}{c}} {\parallel {\rho _k}(0)\parallel }&0& \cdots &0\\ {{K_0}}&{\parallel {\rho _k}(1)\parallel }& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ {{K_0}}&{{K_1}}& \cdots &{\parallel {\rho _k}(T)\parallel } \end{array}} \right]. \end{align} | (A7) |
Since $\Psi_k$ is a lower triangular matrix,all of its eigenvalues will be in unit circle,when $\parallel I - {{{\rm{\tilde B}}}^ + }({{\rm{e}}_k}(t)){\rm{B}}({x_k}(t))\parallel < 1(0 \le t \le T)$ is satisfied. Therefore
$$\parallel \Delta {u_k}(t)\parallel \to 0\;\;{\rm{as}}\;\;k \to \infty ,\quad 0 \le t \le T.$$Then,considering (A3) and condition b) of Lemma 1,we have
$${\pmb x}_k(t)\rightarrow {\pmb x}_d(t) \;\; {\rm as}\;\; k\rightarrow \infty,\quad 0\leq t\leq T.$$ APPENDIX B Proof of Lemma 2[33, 34]Proof. For an arbitrary positive $\varepsilon$,there is a compatible norm $\|\cdot\|_\ast$ which satisfies
$$\|A\|_\ast<\max |\lambda_i|+\varepsilon<\delta+\varepsilon.$$Due to $\delta <1$,we can let the $\varepsilon$ satisfy $\delta+\varepsilon<1$,and let $\gamma=\delta+\varepsilon$,then
$$\|A^k\|_\ast<\underbrace{\|A\|_\ast \cdots \|A\|_\ast}_{k}<\gamma^k<1.$$From the functional analysis,compatible norm satisfies
$$\|A^k\|_2<\sigma \|A^k\|_\ast,$$where $\sigma$ is a positive number which is determined by the relationship between 2-norm and $\ast$-norm.
Then
$$\|A^k\|_2<\sigma\gamma^k.$$| [1] | Xu J X, Bien Z Z. The frontiers of iterative learning control. Iterative Learning Control. Boston: Kluwer, 1998. 9-35 |
| [2] | Bu Xu-Hui, Hou Zhong-Sheng, Yu Fa-Shan, Fu Zi-Yi. Iterative learning control for trajectory tracking of farm vehicles. Acta Automatica Sinica, 2014, 40(2): 368-372 (in Chinese) |
| [3] | Li Z X, Yin C K, Jin S T, Hou Z S. Iterative learning control based automatic train operation with iteration-varying parameter. In: Proceedings of the 10th IEEE International Conference on Control and Automation. Hangzhou, China: IEEE, 2013.51-56 |
| [4] | Hou Z S, Yan J W, Xu J X, Li Z J. Modified iterative-learning-controlbased ramp metering strategies for freeway traffic control with iterationdependent factors. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 606-618 |
| [5] | Arimoto S, Kawamura S, Miyazaki F. Bettering operation of robots by learning. Journal of Robotic Systems, 1984, 1(2): 123-140 |
| [6] | Bristow D A, Tharayil M, Alleyne A G. A survey of iterative learning control. IEEE Control Systems Magazine, 2006, 26(3): 96-114 |
| [7] | Hou Z S, Zhu Y M. Controller-dynamic-linearization-based model free adaptive control for discrete-time nonlinear systems. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2301-2309 |
| [8] | Liu T Q, Wang D W, Chi R H, Shen Q. Neural network based terminal iterative learning control for tracking run-varying reference point. In: Proceedings of the 9th Asian Control Conference. Istanbul, Turkey: IEEE, 2013. 1-5 |
| [9] | Jiang P, Unbehauen R. Iterative learning neural network control for nonlinear system trajectory tracking. Neurocomputing, 2002, 48(1-4): 141-153 |
| [10] | Chi R H, Wang D W, Hou Z S, Jin S T. Data-driven optimal terminal iterative learning control. Journal of Process Control, 2012, 22(10): 2026-2037 |
| [11] | Owens D H, Freeman C T, van Thanh D. Norm-optimal iterative learning control with intermediate point weighting: theory, algorithms, and experimental evaluation. IEEE Transactions on Control Systems Technology, 2013, 21(3): 999-1007 |
| [12] | Lee K S, Lee J H. Convergence of constrained model-based predictive control for batch processes. IEEE Transactions on Automatic Control, 2000, 45(10): 1928-1932 |
| [13] | Shi Jia, Jiang Qing-Yin, Cao Zhi-Kai, Zhou Hua, Gao Fu-Rong. Twodimensional model predictive iterative learning control scheme based on a two-dimensional performance model. Acta Automatica Sinica, 2013, 39(5): 565-573 (in Chinese) |
| [14] | Bu Xu-Hui, Yu Fa-Shan, Hou Zhong-Sheng, Wang Fu-Zhong. Iterative learning control for a class of linear discrete-time switched systems. Acta Automatica Sinica, 2013, 39(9): 1564-1569 (in Chinese) |
| [15] | Xu J X, Tan Y. A composite energy function-based learning control approach for nonlinear systems with time-varying parametric uncertainties. IEEE Transactions on Automatic Control, 2002, 47(11): 1940-1945 |
| [16] | Chi R H, Hou Z S, Xu J X. Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition. Automatica, 2008, 44(8): 2207-2213 |
| [17] | Sun Ming-Xuan, Yan Qiu-Zhen. Error tracking of iterative learning control systems. Acta Automatica Sinica, 2013, 39(3): 251-262 (in Chinese) |
| [18] | Norrlof M, Gunnarsson S. Time and frequency domain convergence properties in iterative learning control. International Journal of Control, 2002, 75(14): 1114-1126 |
| [19] | Paszke W, Galkowski K, Rogers E. Repetitive process based iterative learning control design using frequency domain analysis. In: Proceedings of the 2012 IEEE International Conference on Control Applications. Dubrovnik, Croatia: IEEE, 2012.1479-1484 |
| [20] | Kurek J E, Zaremba M B. Iterative learning control synthesis based on 2-D system theory. IEEE Transactions on Automatic Control, 1993, 38(1): 121-125 |
| [21] | Li X D, Chow T W S, Ho J K L. 2-D system theory based iterative learning control for linear continuous systems with time delays. IEEE Transactions on Circuits and Systems, 2005, 52(7): 1421-1430 |
| [22] | Xu J X. A survey on iterative learning control for nonlinear systems. International Journal of Control, 2011, 84(7): 1275-1294 |
| [23] | Bristow D A, Tharayil M, Alleyne A G. A survey of iterative learning control. IEEE Control Systems Magazine, 2006, 26(3): 96-114 6 |
| [24] | Ahn H S, Chen Y Q, Moore K L. Iterative learning control: brief survey and categorization. IEEE Transactions on Systems, Man, and Cybernetics, 2007, 37(6): 1099-1121 |
| [25] | Hwang D H, Bien Z, Oh S R. Iterative learning control method for discrete-time dynamic systems. IEE Proceedings D: Control Theory & Applications, 1991, 138(2): 139-144 |
| [26] | Sun Ming-Xuan, Huang Bao-Jian. Iterative Learning Control. Beijing: National Defence Industry Press, 1999. 20-105 (in Chinese) |
| [27] | Sun Ming-Xuan, Bi Hong-Bo, Chen Bai-Xia, He Hai-Gang. Learning identification of a class of stochastic time-varying systems with colored noise. Control Theory & Applications, 2012, 29(8): 974-984 (in Chinese) |
| [28] | Chi R H, Hou Z S, Xu J X. Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition. Automatica, 2008, 44(8): 2207-2213 |
| [29] | Yu M, Wang J S, Qi D L. Discrete-time adaptive iterative learning control for high-order nonlinear systems with unknown control directions. International Journal of Control, 2012, 10(6): 1111-1118 |
| [30] | Li X D, Xiao T F, Zheng H X. Adaptive discrete-time iterative learning control for non-linear multiple input multiple output systems with iteration-varying initial error and reference trajectory. IET Control Theory & Applications, 2011, 5(9): 1131-1139 |
| [31] | Narendra K S, Xiang C. Adaptive control of discrete-time systems using multiple models. IEEE Transactions on Automatic Control, 2000, 45(9): 1669-1686 |
| [32] | Li X L, Zhang W. Multiple model iterative learning control. Neurocomputing, 2010, 73(13-15): 2439-2445 |
| [33] | Huang Lin. Linear Algebra in System and Control Theory. Beijing: Science Press, 1984. 250-251 (in Chinese) |
| [34] | Li Xiao-Li, Wang Wei. Multiple model switching controller for discretetime system. Journal of Northeastern University (Natural Science), 1999, 20(5): 468-469 (in Chinese) |
 2014, Vol.1
2014, Vol.1 


