2. Science and Technology on Space Intelligent Control Laboratory, Beijing Institute of Control Engineering, Beijing 100190, China
Distributed control of networked robotic manipulators has gained significant attention in recent years. The motivation of the research is that a multi-robot approach offers several advantages, such as parallel execution of tasks,robustness by adding redundancy,and elimination of the single point of failure that is present in single robot systems[1],etc. The major purpose of distributed control is to achieve a global group behavior with only local interaction. Distributed control scheme performed on multi-robot networks can provide great benefits with lower cost, higher versatility and easier maintenance[2]. Consensus,as a fundamental problem in distributed control,means that a group of vehicles reach an agreement on a common value by interacting with their local neighbors.
The robotic agent in this paper is modeled as the fully actuated Euler-Lagrange system. The studies on distributed control of multiple Euler-Lagrange systems mainly focus on the position coordination problems[3, 4, 5, 6, 7, 8, 9, 10]. The consensus tracking problem with a single or multiple dynamic leaders is considered in [6, 7, 8, 10]. In [6],a unified extended Slotine and Li controller is proposed for both leaderless consensus and consensus tracking in the presence of dynamic uncertainties on directed graphs with a spanning tree. Cascaded framework is introduced which provides a convenient approach to handle the consensus problem. Yet,for the tracking case,the desired trajectory is assumed to be available to all the agents. To remove this assumption,a distributed sliding mode estimator which aims at estimating the desired trajectory in a distributed manner is constructed in [7] for multiple linear agents,and then extended to multiple Euler-Lagrange systems with dynamic uncertainties in [8] for directed graphs containing a spanning tree. The work of [9] develops the cascaded framework in [6],and solves task-space consensus problem on strongly connected graphs. The work of [10] further proposes an adaptive task-space position observer such that task-space velocity-free synchronization on directed graphs containing a spanning tree can be achieved.
Nevertheless,the above literature concentrates on the distributed position control in free space without considering the case when the robots interact with the environment. In practical applications,such as inspection,assembly,polishing,grinding as well as scribing,the end-effectors of the robot manipulators are usually required to be in contact with the environment,which involves the interactive force between the manipulators and the environment. In order to realize safe and elaborate operation in the presence of uncertainties,various adaptive force/position control laws are developed for single robotic agent[11, 12, 13, 14, 15], aiming at controlling both the position of the end-effector in the unconstrained direction and its contact force with the environment in the constrained direction. Adaptive force control is proposed in [11] to estimate unknown environment stiffness with exact environment position when the robot inertia matrix is constant. In [12],adaptive control is also used to deal with stiffness uncertainties after fully linearizing and decoupling system dynamics. The work of [13] proposes a passivity-based adaptive law to cope with stiffness uncertainties of the environment by use of a scalar factor,while the robot model and surface position are required to be exactly known. The work of [14] takes both stiffness uncertainties and surface kinematic uncertainties into account,and devises a new adaptive force/position tracking controller for a soft robot finger in compliant contact with a rigid flat surface when the dynamic parameters of the robot are exactly known.
When it comes to large-scale assembly tasks in modern manufactures and space applications,multiple robot manipulators may perform tasks in a common environment and the research of distributed force control becomes as significant as distributed motion control in these cases. Another example is that when multi-robots push or carry a common flat object,they must coordinate both position and force to realize movement of the object without rotating or tumbling. Therefore,it is necessary to consider the force synchronization problem in many applications due to the requirement of a balanced movement. The work of [15] considers multiple mobile manipulators grasping a common object in contact with a rigid surface,and proposes an adaptive robust control law in a cooperative manner,but not in a distributed manner. In addition,when the environment is compliant,the methods in rigid condition are no longer applicable,since the bouncing effect caused by the contact force can eventually lead to instability of the manipulators[16]. To our best knowledge,no work has focused on distributed compliant force control of networked robotic manipulators. When the information topology is directed with a spanning tree and uncertain environment and robotic dynamics are considered,due to the asymmetric Laplacian matrix, the nonlinearities and uncertainties of the robot-environment model,the distributed force control scheme is not a straightforward extension of the single agent case.
In this paper,we consider the force synchronization problem in constrained space,where multiple robotic manipulators on directed graphs interact with uncertain compliant environment. We propose a distributed adaptive hybrid controller such that force and free-space position asymptotically synchronize to the convex hull constituted by the leaders under directed graphs containing a spanning tree. A novel adaptive force observer is constructed to achieve force synchronization in the presence of environment uncertainties,which further removes the requirement to measure force derivatives. In addition,by defining an appropriate force reference signal,our strategy eliminates the reliance on the estimation of surface distance,thus avoiding overparamterization in the kinematic loop design. The proposed scheme has a quite simple and direct form in a cascaded framework.
Notation. In the subsequent sections,if there are no special illustrations,$(\hat { \cdot })$ denotes the estimation of ($\cdot$),$(\tilde { \cdot }) = (\hat { \cdot })-( \cdot )$, and $\Delta ( \cdot ) = ( \cdot )-( \cdot )_d $ with $( \cdot )_d $ being the desired value of $( \cdot )$. In addition,${\bf 1}_m$ and $0_m$ denote $m\times1$ column vector containing all ones and all zeros respectively,and ${I}_m$ denotes the $m\times m$ identity matrix.
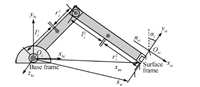
Ⅱ. PRELIMINARIES AND PROBLEM DESCRIPTION A. Robotic Dynamics and KinematicsWe consider $m$ robotic followers labeled as agents 1 to $m$, interacting with flat compliant environment. The single-agent model is illustrated in Fig. 1. The dynamic model of the $i$th follower in joint space ignoring friction forces can be written as[14]
|
Download:
|
| Fig. 1 A robot manipulator interacting with a flat compliant surface. | |
| $ \begin{align} M_i({\pmb q}_i)\ddot {\pmb q}_i + C_i({\pmb q}_i,\dot {{\pmb q}}_i)\dot {{\pmb q}}_i + {\pmb g}_i({\pmb q}_i) + J_i({\pmb q}_i)^{\rm T}{\pmb n}_{si}f_i = {\pmb \tau}_i, \end{align} $ | (1) |
where $\pmb q_i\in R ^p$ is the joint variable,$M_i(\pmb q_i) \in R ^{p\times p}$ is the inertia matrix,$C_i(\pmb q_i$,$\dot {\pmb q}_i) \in R ^{p\times p}$ is the coupled centripetal and Coriolis matrix,${\pmb g}_i(\pmb q_i)\in {\bf R}^p$ is the gravitational force,$\pmb {\tau}_i \in R ^p$ is the exerted joint control torque,$J_i(\pmb q_i)$ is the Jacobian matrix which will be defined later,$f_i\in R$ is the normal contact force,and $\pmb n_{si}\in R^3 $ is the surface normal vector.
Let $x_{bi}$-${y}_{bi}$-${z}_{bi}$ and ${ x}_{ei}$-${y}_{ei}$-${z}_{ei}$ be the base frame,and the surface frame,respectively,and $R_i\in R ^{\rm{3\times 3}}$ be the rotation matrix from the base frame to the surface frame. Let ${\pmb x}_{si} \in R ^{\rm 3}$ and ${\pmb x}_{i} \in R ^{\rm 3}$ denote the surface/environment position and the generalized end-effector position,respectively. The afore-mentioned variables are illustrated in Fig. 1,where ${\pmb x}_i$ is shown as ${\pmb x}_{mi}$. Clearly,we have $ R^{\rm T}_i{\pmb n}_{si} =[1 0 0]^{\rm T}$. According to [17], ${\pmb x}_i$ can be expressed as
| $ \begin{align} {\pmb x}_i = {\pmb h}_i({\pmb q}_i), \end{align} $ |
where ${\pmb h}_i( \cdot ): \in R^p \to R ^3$ is a nonlinear mapping from joint space to task space. Then,the end-effector velocity $\dot {\pmb x}_i$ is related to the joint-space velocity as[18]
| $ \begin{align} \dot {{\pmb x}}_i = J_i({\pmb q}_i)\dot {{\pmb q}}_i, \end{align} $ |
where $J_i({\pmb q}_i)\in R^{3\times p}$ is referred to as the Jacobian matrix. For simplicity of analysis,we make the following assumption.
Assumption 1. The robot manipulators are operated in finite task space,and are non-redundant,i.e.,$J_i({\pmb q}_i)$,$i=1, \cdots,m$,are nonsingular and square matrices.
We proceed to get the deformation of the compliant environment as[14]
| $ \begin{align} \delta x_{fi} = {\pmb x}_i^{\rm T} {\pmb n}_{si}-{\pmb x}_{si}^{\rm T} {\pmb n}_{si}, \end{align} $ |
which is assumed to be linearly elastic with environment stiffness $k_{si}$,i.e., ${\delta x}_{fi} = \theta _{0i}f_i$,where $\theta _{0i} = \frac{1}{k_{si} }$. The distance from the base center to the surface is presented as $\theta _{1i} = {\pmb x}_{si}^{\rm T} {\pmb n}_{si}$.
Let $\bar{\pmb x}_i $ be the task-space position vector in the surface frame. Then, we have
| $ \begin{align} \bar{\pmb x}_i = R_i^{\rm T}{\pmb x}_i-\left[ {{\begin{array}{*{20}c} {\theta _{1i} } \\ 0_2 \\ \end{array} }} \right], \end{align} $ | (2) |
and the task-space velocity
| $ \begin{align} {\dot {\bar {\pmb x}}}_i=\bar J_i(\pmb{q}_i)\dot {\pmb q}_i, \end{align} $ | (3) |
where $\bar J_i(\pmb{q}_i)= R_i^{\rm T} J_i(\pmb{q}_i)$ is the Jacobian matrix in the surface frame. Therefore,$\bar {\pmb x}_i$ is partitioned into two parts,i.e.,
| $ \begin{align} \bar {\pmb x}_i = \left[{{\begin{array}{*{20}c} {{\bar x}_{fi} } \\ {{\bar {\pmb x}}_{pi} } \\ \end{array} }} \right], \end{align} $ |
where ${\bar x}_{fi}=\delta x_{fi}$ is the environment deformation in the constrained space utilized for force tracking, and $\bar {\pmb x}_{pi} $ is the position in the unconstrained space utilized for motion tracking.
As a result,(1) can be reformulated as
| $ \begin{align} M_i(\pmb q_i){\ddot {\pmb q}}_i + C_i(\pmb q_i,{\dot {\pmb q}}_i){\dot {\pmb q}}_i + \pmb g_i(\pmb q_i) + \bar J^{\rm T}_i \left[{{\begin{array}{*{20}c} f_i \\ 0_2 \\ \end{array} }} \right] = \pmb{\tau}_i. \end{align} $ | (4) |
It is well known that the dynamics (4) have the following properties[18].
Property 1. There exist positive constants ${k_{m1}}$,$ {k_{m2}}$,${k_C}$ and ${k_g}$ such that ${k_{m1}}I_p \le M_i(\pmb q_i)\le {k_{m2}}I_p$,$\left\|C_i(\pmb y_1,\pmb y_2)\pmb y_3 \right\|\le {k_C} \left\|\pmb y_2 \right\|\left\|\pmb y_3 \right\|$ for all vectors $\pmb y_1$,$\pmb y_2$ and $\pmb y_3\in R^p$,and $\left\|\pmb g_i(\pmb q_i) \right\|\le {k_{g}}$.
Property 2. The dynamics (4) is linearly parametric with respect to a group of unknown dynamic parameters $\pmb a_{di} \in R ^r$,i.e.,
| $ \begin{align} M_i(\pmb q_i)\pmb {\xi}_1 + C_i(\pmb q_i,\dot{\pmb{q}}_i) \pmb{\xi}_2 + \pmb g_i(\pmb q_i) = Y_{di} (\pmb q_i,\dot{\pmb{q}}_i,\pmb{\xi}_2,\pmb{\xi}_1)\pmb a_{di}, \end{align} $ |
where $Y_{di} \in R^{p\times r}$ is the dynamic regressor matrix, $\pmb{\xi}_1\in R^p$,and $\pmb{\xi}_2\in R^p$.
Property 3. $\dot M_i(\pmb q_i)-2C_i(\pmb q_i$,${\dot {\pmb q}}_i)$ is skew symmetric if $C_i(\pmb q_i$,${\dot {\pmb q}}_i)$ is appropriately selected.
B. Graph TheoryWe assume there are $N$ agents with $m$ robotic followers and $N-m$ virtual leaders. Let the vertex $i$ denote the $i$th agent and the vertex set $\mathcal {V}=\left\{ 1 \right.$,$\cdots$, $\left. N \right\}$. The edge $(i$,$j)$ denotes the information flow between agents $i$ and $j$. Let $\mathcal E$ denote the edge set. An edge $(j$,$i) \in \mathcal {E}$ means that agent $i$ can obtain information from agent $j$. The vertex sets for the followers and leaders are denoted by $\mathcal {V}_F=\left\{ 1 \right.$,$\cdots$,$\left. m \right\}$ and $\mathcal {V}_L=\left\{m+1 \right.$,$\cdots$,$\left. N \right\}$, respectively. The following assumption is made for the information topology.
Assumption 2. For each follower,there exists at least one leader that has a directed path to the follower.
The adjacency matrix $\mathcal { W} = [w_{ij}] \in {\bf R}^{N\times N}$ associated with the interaction graph $\mathcal {E} $ is defined as $w_{ij} > 0$ if $(j$,$i) \in \mathcal {E}$, and $w_{ij} = 0$,otherwise. We assume the self edges do not exist,i.e.,$w_{ii} = 0$. Then we define the Laplacian matrix $L=[\ell_{ij}]\in R^{N\times N}$ as
| $ \begin{align*} \ell_{ij}=\begin{cases}\sum\limits_{k=1}^N w_{ik},&i=j,\\ -w_{ij},&i\ne j.\end{cases} \end{align*} $ |
Here,$L$ has the form of[8]
| $ \begin{align} L = \left[{{\begin{array}{*{20}c} {L_1 } & {L_2 } \\ {0_{(N-m)\times m} } & {0_{(N-m)\times (N-m)} } \\ \end{array} }} \right], \end{align} $ | (5) |
where $L_1 \in R^{m\times m}$ and $L_2 \in R^{m \times (N-m)}$ satisfy the following lemma.
Lemma 1[8]. The matrix $L_1$ is non-singular,and all eigenvalues of $L_1$ have positive real parts,if and only if Assumption 2 holds. Moreover,each entry of $-L_1^{-1} L_2 $ is nonnegative,and all row sums of $-L_1^{-1} L_2 $ equals to one,if Assumption 2 holds.
In this paper,for the robotic followers represented by (3) and (4) with the uncertainties of dynamic parameter ${\pmb a}_{di}$, environment stiffness $k_{si}$ and distance $\theta_{1i}$,our control objective is to drive both $f_i$ and $\bar{\pmb x}_{pi}$ to their desired values $f_{di}$ and $\bar{\pmb x}_{pdi}$ by designing ${\pmb \tau}_i$ in a distributed manner,where $f_{di}$ and $\bar{\pmb x}_{pdi}$ are determined by the convex hull spanned by the leaders,i.e.,
| $ \begin{align} &\pmb f_d :=\left[{{\begin{array}{*{20}c} {f_{d1} } & \cdots & {f_{dm}} \\ \end{array} }} \right]^{\rm T} =-(L_1^{-1} L_2)\pmb f_L,\\ \end{align} $ | (6) |
| $ \begin{align} &\bar{\pmb x}_{pd} := \left[{{\begin{array}{*{20}c} {\bar{\pmb x}_{pd1}^{\rm T} } & \cdots & {\bar{\pmb x}_{pdm}^{\rm T} } \\ \end{array} }} \right]^{\rm T} =-(L_1^{-1} L_2 \otimes {\rm I}_2 )\bar{\pmb x}_{pL}, \end{align} $ | (7) |
where $\pmb f_L$ and $\bar{\pmb x}_{pL}$ are the column stack vectors of $f_i$ and $\bar{\pmb x}_{pi}~(i\in \mathcal {V}_L)$, respectively. To guarantee the convergence of sliding mode estimators,we introduce the following assumption[7].
Assumption 3. $\pmb f_L$ and $\bar{\pmb x}_{pL}$ as well as their first-order,second-order and third-order derivatives are all bounded.
Ⅲ. THE DESIGN OF FORCE/POSITION CONSENSUS TRACKING CONTROLLERIn this section,we give the cascaded structure design scheme, which divides the overall system into kinematic module and dynamic module. The kinematic loop is first constructed to achieve force/position synchronization and to get a reference joint-space velocity for the controller,while the dynamic loop is to pose the control law such that the conditions required for the kinematic loop design are satisfied.
A. Kinematic Loop DesignIn this part,for the kinematic equation (3) in the presence of uncertain environment stiffness $k_{si}$ and distance $\theta_{1i}$,we aim at designing an appropriate joint-space reference velocity such that $f_i\to f_{di}$ and ${\bar{\pmb x}}_{pi}\to {\bar {\pmb x}}_{pdi}$ as $t \to \infty$,$\forall i \in \mathcal {V} _F$,and giving the design conditions,which will be satisfied by the dynamic loop.
We first construct the sliding mode estimators to estimate the desired trajectory in a distributed manner[7],i.e.,
| $ \begin{align} &\dot {\hat{ v}}_{fi} =-\beta _{f1} {\rm sgn}\left[ {\sum\limits_{j \in \mathcal {V}_F} {w_{ij} (\hat{v}_{fi}- \hat{v}_{fj} ) + \sum\limits_{j \in \mathcal {V} _L} {w_{ij} (\hat{v}_{fi}-\dot {f}_j )} } } \right],\end{align} $ | (8) |
| $ {{\dot{\hat{v}}}_{pi}}=-{{\beta }_{p1}}\text{sgn}\left[\sum\limits_{j\in {{\nu }_{F}}}{{{w}_{ij}}({{{\hat{v}}}_{pi}}-{{{\hat{v}}}_{pj}})+\sum\limits_{j\in {{\nu }_{L}}}{{{w}_{ij}}({{{\hat{v}}}_{pi}}-{{\overset{.}{\mathop{{\bar{x}}}}\,}_{pj}})}} \right], $ | (9) |
| $ \begin{align} & \dot {\hat{a}}_{fi} =-\beta _{f2} {\rm sgn}\left[ {\sum\limits_{j \in \mathcal {V} _F } {w_{ij} (\hat{a}_{fi}- \hat{a}_{fj} ) + \sum\limits_{j \in \mathcal {V} _L } {w_{ij} (\hat{a}_{fi}-\ddot {f}_j )} } } \right],\\\end{align} $ | (10) |
| $ \begin{align} &\dot {\hat{\pmb a}}_{pi} =-\beta _{p2} {\rm sgn}\left[ {\sum\limits_{j \in \mathcal {V} _F } {w_{ij} (\hat{\pmb a}_{pi}- \hat{\pmb a}_{pj} ) + \sum\limits_{j \in \mathcal {V} _L } {w_{ij} (\hat{\pmb a}_{pi}-\ddot {\bar {\pmb x}}_{pj} )} } } \right], \end{align} $ | (11) |
where $\hat v_{fi}$ and $ \hat {\pmb v}_{pi}$ are estimates of $\dot f_{di}$ and $\dot {\pmb x}_{pdi}$,respectively,$\hat a_{fi}$ and $ \hat {\pmb a}_{pi}$ are estimates of $\ddot f_{di}$ and $\ddot {\bar {\pmb x}}_{pdi}$,respectively,$\beta _{f1}$, $\beta _{p1}$,$\beta _{f2}$ and $\beta _{p2}$ are adjustable positive constant gains designed to satisfy the following condition.
Condition 1. $\beta _{f1} > \| {\ddot {f}_d }\|$,$\beta _{p1} > \left\| {\ddot {\bar {\pmb x}}_{pd} } \right\|$,$\beta _{f2} > \left\| {\dddot {f}_d } \right\|$ and $\beta _{p2} > \left\| {\dddot {\bar {\pmb x}}_{pd} } \right\|$.
Under Condition 1,the sliding mode estimators are ensured to converge in finite time $T_0$[7].
Then,for $i \in \mathcal {V} _F$, we design the estimated joint-space reference velocity based on the estimated desired trajectory
| $ \begin{align} \hat {\dot {{\pmb q}}}_{ri} = \bar J_i^{-1} \hat {\dot {\bar {\pmb x}}}_{ri}, \end{align} $ | (12) |
where
| $ \begin{align} &\hat { {\dot {\bar {\pmb x}}}}_{ri} = \hat {\pmb v}_{ \bar {x}_{oi}}-\\ &\qquad \Lambda_i \left[{{\begin{array}{*{20}c} { \hat {\theta }_{0i} [\sum\limits_{j \in \mathcal {V} _F} {w_{ij} (f_{oi}-f_{oj} )}-{\sum\limits_{j \in \mathcal {V} _L } {w_{ij} (f_{oi}-f_{j})}}]} \\ {\sum\limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L } {w_{ij} ({\bar {\pmb x}}_{pi}-{\bar {\pmb x}}_{pj} )} } \\ \end{array} }} \right], \end{align} $ | (13) |
| $ \begin{align} &\hat {\pmb v}_{ \bar {x}_{oi}} = [{\begin{array}{*{20}c} {\hat {\theta}} _{0i} \hat {v}_{fi} & {\hat {\pmb v}}_{pi} ^{\rm T} \\ \end{array} }]^{\rm T},\end{align} $ | (14) |
| $ \begin{align} &\dot {\hat {\theta }}_{0i} = \Gamma _{0i}(\dot f_{oi}+\Lambda_{oi}(f_{oi}-f_i))(f_{oi}-f_i),\\ \end{align} $ | (15) |
| $ \begin{align} & \dot {f}_{oi} =\frac{\dot {\bar {x}}_{fi} }{\hat {\theta} _{0i} }-\Lambda _{oi} (f_{oi}-f_i). \end{align} $ | (16) |
Here,$f_{oi}$ is the observed force,and $\hat { {\dot {\bar {\pmb x}}}}_{ri}$ is the estimated task-space reference velocity. Equation (15) is the environment stiffness adaptation law. The estimated stiffness parameter $\hat {\theta}_{0i}$ is assumed to be nonsingular in the whole updating process. Equation (16) is the decentralized force observer to obtain the filtered $f_i$. $\Lambda_i={\rm {diag}}\{\Lambda _{fi},\Lambda _{pi}\}$,where $\Lambda _{fi}$ and $\Lambda _{pi}$ are adjustable positive definite diagonal matrices. $\Gamma _{0i}$ is the adjustable positive definite updating gain,and $\Lambda_{oi}$ is the adjustable positive observer gain. $\dot {\bar {x}}_{fi}$ in (16) is the projection of $\dot {\bar {\pmb x}}_i$ in the force direction,and $\dot {\bar {\pmb x}}_i$ can be derived from (3).
Now,we proceed to analyze quality of the kinematic loop. The following lemmas will be adopted.
Lemma 2[19]. Let $\pmb y = G(p_1)\pmb u$,where $G(p_1)$ is an $m_1\times n_1$ strictly proper and exponentially stable transfer matrix with the Laplace variable $p_1$. Then ${\pmb u}(t) \in \mathcal L_2^{n_1}$ implies ${\pmb y}(t) \in \mathcal L_2^{m_1} \cap \mathcal L_\infty ^{m_1}$,$\dot {\pmb y}(t) \in \mathcal L_2^{m_1}$,${\pmb y}(t)$ is continuous and ${\pmb y}(t) \to 0$ as $t \to \infty$.
Lemma 3[19]. If $\pmb y\in \mathcal L_2$ is uniformly continuous,then $\pmb y\to 0$ as $t\to \infty$.
Denote the estimated joint-space sliding mode vector and the estimated task-space sliding vector respectively as
| $ \begin{align} \hat {\pmb s}_i=\dot {\pmb q}_i-\hat {\dot {\pmb q}}_{ri} \end{align} $ | (17) |
and
| $ \begin{align} \hat {\pmb s}_{\bar {x}i} = {\dot {\bar {\pmb x}}}_i-\hat {\dot {\bar {\pmb x}}}_{ri}. \end{align} $ | (18) |
Obviously,from (3),(12),(17) and (18),we have
| $ \begin{align} \hat {\pmb s}_i=\bar J_i^{-1}\hat {\pmb s}_{\bar xi}. \end{align} $ | (19) |
Here,$\hat {\dot {\pmb q}}_{ri}$ and $\hat {\pmb s}_i$ will be used later in Section III-B for the dynamic loop design.
Substituting (13) and (16) into (15),we get
| $ \begin{align} \hat {\pmb s}_{\bar {x}i} = \left[{{\begin{array}{*{20}c} { \hat {\theta }_{0i}(\dot f_{oi}-\dot f_{ri}) } \\ \dot {\bar {\pmb x}}_{pi}-\dot {\bar {\pmb x}}_{pri} \\ \end{array} }} \right] +\Lambda_{oi} \left[{{\begin{array}{*{20}c} { \hat {\theta }_{0i}(f_{oi}-f_{i}) } \\ 0_2 \\ \end{array} }} \right], \end{align} $ | (20) |
where
| $ \begin{align} &\dot f_{ri}=\hat v_{fi}-\Lambda _{fi}[\sum\limits_{j \in \mathcal {V} _F} {w_{ij} (f_{oi}-f_{oj} )}-{\sum\limits_{j \in \mathcal {V} _L } {w_{ij} (f_{oi}-f_{j})}}],\\ &\dot {\bar {\pmb x}}_{pri}= {\hat {\pmb v}}_{pi}-\Lambda _{pi}\sum\limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L } {w_{ij} (\bar {\pmb x}_{pi}-\bar {\pmb x}_{pj} )}. \end{align} $ |
Let $\Delta f_{oi}=f_{oi}-f_{di}$. Then,(20) can be rewritten as
| $ \begin{align} &\left[{{\begin{array}{*{20}c} {\hat {\theta }_{0i} \Delta \dot {f}_{oi} } \\ {\Delta \dot {\bar {\pmb x}}_{pi} } \\ \end{array} }} \right] =-\Lambda _{i} \left[{{\begin{array}{*{20}c} {\hat {\theta }_{0i} \sum\limits_{j \in \mathcal {V} _F} {w_{ij} (f_{oi}-f_{oj} )} } \\ {\sum\limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L} {w_{ij}(\bar {\pmb x}_{pi}-\bar {\pmb x}_{pj} )} } \\ \end{array} }} \right]-\\ &\qquad \Lambda _{i} \left[{{\begin{array}{*{20}c} {\hat {\theta }_{0i}{\sum\limits_{j \in \mathcal {V} _L } {w_{ij} (f_{oi}-f_{j})}} } \\ {0_2 } \\ \end{array} }} \right] +\pmb{\sigma}_i, \end{align} $ | (21) |
where
| $ \begin{align} {\pmb{\sigma}} _i = \left[ {{\begin{array}{*{20}c} {\hat {\theta }_{0i} (\hat {v}_{fi}-\dot {f}_{di} )} \\ {\hat {\pmb v}_{pi}-\dot {\bar {\pmb x}}_{pdi} } \\ \end{array} }} \right]-\Lambda_{oi}\left[{{\begin{array}{*{20}c} { \hat {\theta }_{0i}(f_{oi}-f_{i}) } \\ 0_2 \\ \end{array} }} \right]+ \hat {\pmb s}_{\bar {x}i}. \end{align} $ |
Quality of the kinematic loop is given in the following theorem.
Theorem 1. For the system constituted by (15),(16),(8), (9) and (21),if Assumptions 2 and 3,Condition 1 and the following Condition 2 hold,then $\Delta f_i\to 0$ and $\Delta \bar {\pmb x}_{pi}\to 0$ as $t \to \infty$.
Condition 2. For $t\le T_0$,$\hat {\pmb s}_{\bar xi} \in \mathcal L_\infty$; for $t>T_0$,$\hat {\pmb s}_{\bar xi} \in \mathcal L_2 \cap \mathcal L_\infty$.
Proof. We first concentrate on the proof of convergence in the force direction. Let us begin with analysis of the observer dynamic loop constituted by (15) and (16). Denote $\bar x_{foi}=\theta_{0i}f_{oi}$ and $\tilde {\bar x}_{foi}=\bar x_{foi}-\bar x_{fi}$. Then,multiplying $\hat \theta_{0i}$ on both sides of (16) and by simple transformation,we can rewrite (16) as
| $ \begin{align} \dot {\tilde {\bar x}}_{foi}=-\Lambda_{oi}{\tilde {\bar x}}_{foi}-\tilde \theta_{0i}(\dot f_{oi}+\Lambda_{oi}(f_{oi}-f_i)). \end{align} $ | (22) |
The Lyapunov function $V_{fi}$ is then constructed for the observer dynamics as
| $ \begin{align} V_{fi} = \frac{1}{2}{\tilde {\bar x}}_{foi}^{\rm T}{\tilde {\bar x}}_{foi} + \frac{\theta _{0i} }{2}\tilde {\theta }_{0i} ^{\rm T}\Gamma _{0i}^{-1} \tilde {\theta }_{0i}. \end{align} $ | (23) |
Differentiating $V_{fi}$ with respect to time and substituting (15) and (22) into it,we obtain
| $ \begin{align} \dot V_{fi} =-{\tilde {\bar x}}_{foi}^{ \rm T}\Lambda_{oi}{\tilde {\bar x}}_{foi}\le0. \end{align} $ | (24) |
This indicates that ${\tilde {\bar x}}_{foi}\in \mathcal L_2\cap \mathcal L_\infty$ and $\tilde \theta_{0i}\in \mathcal L_\infty$. Therefore, we have $f_{oi}-f_i\in \mathcal L_2\cap \mathcal L_\infty$ and $\hat \theta_{0i}\in \mathcal L_\infty$.
Now,we continue to prove the boundedness of $\Delta f_i$ in finite time for bounded initial values $\Delta f_i(0)$,$\hat {\theta}_{0i}(0)$ and ${\hat {v}}_{fi} (0)$. If Condition 1 holds, (8) guarantees that $\left\| {\hat {v}_{fi}-\dot {f}_{di}} \right\| \to 0$ in finite time $T_0$[8]. Meanwhile,$\hat {v}_{fi} \in \mathcal L_\infty$ can be ensured,provided that Assumption 3 holds. For bounded $\Delta f_i$,we have bounded $f_i$ and then bounded $f_{oi}$. Thus,$\dot f_{ri}$ is bounded. Since we have $\hat {\pmb s}_{\bar x_i} \in \mathcal L_\infty$ from Condition 2 and $f_{oi}-f_i\in \mathcal L_\infty$ from the above observer loop analysis,$\dot f_{oi}\in \mathcal L_\infty$ is guaranteed based on (20). From (22),we can further obtain that $\dot f_{oi}-\dot f_i\in \mathcal L_\infty$. Then,$\Delta {\dot f_i}\in \mathcal L_\infty$. Therefore,we can conclude that $\Delta {f_i}$ is bounded in finite time $T_0 $.
When $t>T_0$,Condition 2 gives $\hat {\pmb s}_{\bar x} \in \mathcal L_2$,and thus $\pmb{\sigma}_i\in \mathcal L_2$. From (21),we get $\Delta \dot f_o+\Lambda_fL_1\Delta f_o\in \mathcal L_2$,where $\Delta f_o$ is the stack vector of $\Delta f_{oi}$, and $\Lambda_f={\rm {diag}}\{\Lambda_{f1}$,$\cdots$, $\Lambda_{fm}\}$. Since $-L_1$ is Hurwitz according to Assumption 2 and Lemma 1,$\Delta f_{oi}\in \mathcal L_2\cap \mathcal L_\infty$ and $\Delta \dot f_{oi}\in \mathcal L_2\cap \mathcal L_\infty$ are derived from the input-output stability analysis in Lemma 2. Then we have $\Delta f_i=\Delta f_{oi}-(f_{oi}-f_i)\in \mathcal L_2\cap \mathcal L_\infty$ and $\Delta \dot f_i\in \mathcal L_\infty$. From Lemma 3,the uniform continuity of $\Delta f_i$ and the result that $\Delta f_i\in \mathcal L_2$ determine that $\Delta {f_i} \to 0$ as $t \to \infty $ .
Similar to the stability analysis in the force direction, we can get that $\Delta {\bar {\pmb x}}_{pi} \to 0$ as $t \to \infty$.
Remark 1. Our construction of the decentralized force observer (16) not only removes the requirement for the measurements of force derivatives,but also provides a simple and direct solution to the force synchronization problem with environment uncertainties under directed graphs containing a spanning tree. In fact,if we do not introduce (16),the reference task-space velocity is still constructed as (13) with $f_{oi}$ replaced by $f_{i}$,i.e.,
| $ \begin{align} \hat {\dot {\bar {\pmb x}}}_{ri} = \hat {\pmb v}_{ \bar {x}_{oi}}- \Lambda_i \left[{{\begin{array}{*{20}c} { \hat {\theta }_{0i} \sum\limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L } {w_{ij} (f_{i}-f_{j} )} } \\ {\sum\limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L } {w_{ij} (\bar {\pmb x}_{pi}-\bar {\pmb x}_{pj} )} } \\ \end{array} }} \right], \end{align} $ | (25) |
where $\hat {\theta}_{0i}$ should be updated online by a new adaptation law derived from Lyapunov stability tool or input-output stability analysis.
Substituting (25) into (18),we get the closed-loop kinematic equation
| $ \begin{align} \Delta \dot {\bar {\pmb x}}=-\Lambda(L_1\otimes I_3)\Delta{\bar {\pmb x}}+\hat {\pmb s}_{\bar x}+\tilde \theta_0\pmb Y_s+(\pmb v_{\bar {\pmb x}_o}-\dot {\bar {\pmb x}}_d), \end{align} $ | (26) |
where $\Delta \bar {\pmb x}$,$\hat {\pmb s}_{\bar x}$,$\pmb v_{\bar x_o}$ and $\pmb Y_s$ are the column stack vectors of $\Delta \bar {\pmb x}_i$,$\hat {\pmb s}_{\bar x_i}$,$\pmb v_{\bar x_{oi}}$ and $\pmb Y_{si}$,respectively,$ \pmb Y_{si}= [ -\hat{v}_{fi} +\Lambda _{fi} \sum \limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L} w_{ij} (f_{i}-f_{j}),0_2^{\rm T}] ^{\rm T} $,$\tilde{\theta}_0= {\rm diag}\{{\tilde {\theta}_{01}\otimes I_3,\cdots,\tilde{\theta}_{0 m} \otimes I_3}\}$ and $\Lambda=\rm {diag}\{\Lambda_1$, $\cdots$,$\Lambda_m\}$. Since the matrix $L_1$ is asymmetric in (26),we cannot obtain the asymptotic convergence of tracking error $\Delta {\bar {\pmb x}}$ via the traditional Lyapunov tool. If we turn to input-output stability analysis,$\tilde {\theta}_{0} \pmb Y_s\in \mathcal L_2$ must be guaranteed to get an asymptotically convergent $\Delta {\bar {\pmb x}}$. However,it is difficult for us to construct an indirect stiffness updating law satisfying $\tilde {\theta}_{0} \pmb Y_s\in \mathcal L_2$. Therefore,the straightforward extension of traditional tools for consensus tracking problem is not applicable to solve the force synchronization problem with the asymmetric $L_1$ and the term $\tilde \theta_0\pmb Y_s$ introduced by uncertain stiffness $k_{si}$. Then,the force observer (16) is proposed in our paper to deal with the afore-mentioned problem,where the stiffness uncertainty is first coped with in the observer loop (22) via Lyapunov tool,and then,synchronization is achieved in the kinematic loop (21) via input-output stability analysis.
B. Dynamic Loop DesignIn this part,we will devise the control law $\tau_i$ for (3) such that not only Condition 2 for the kinematic loop design is satisfied,but the velocity tracking errors of all the robotic followers are also driven to zero,i.e.,
| $ \begin{align} \hat {\pmb s}_{\bar xi} \in \left\{ {{\begin{array}{*{20}c} {\mathcal L_\infty,{\begin{array}{*{20}c} & {t \le T_0 },\\ \end{array} }} \\ {\mathcal L_2 \cap \mathcal L_\infty,{\begin{array}{*{20}c} {t > T_0 },\\ \end{array} }} \\ \end{array} }} \right. \end{align} $ |
$\Delta \dot f_i \to 0$ and $\Delta \dot {\bar {\pmb x}}_{pi} \to 0$ as $t\to 0$,$\forall i\in \mathcal V_F$.
Now,it is time for us to design the adaptive control law. On the basis of (12) and (13),we define the estimated task-space reference acceleration as
| $ \begin{align} & \hat {\ddot {\bar {\pmb x}}}_{ri} = \left[ {{\begin{array}{*{20}c} {\hat {\theta }_{0i} \hat {a}_{fi} } \\ {\hat {\pmb a}_{pi} } \\ \end{array} }} \right] + \left[{{\begin{array}{*{20}c} {\dot {\hat {\theta }}_{0i} \dot f_{ri} } \\ 0_2 \\ \end{array} }} \right]-\\ &\qquad \Lambda_i \left[{{\begin{array}{*{20}c} {\hat {\theta }_{0i} [\sum\limits_{j \in \mathcal {V} _F} {w_{ij} (\dot f_{oi}-\dot f_{oj} )}-{\sum\limits_{j \in \mathcal {V} _L } {w_{ij} (\dot f_{oi}-\dot f_{j})}}] } \\ {\sum\limits_{j \in \mathcal {V} _F \cup \mathcal {V} _L } {w_{ij} (\dot{\bar{\pmb x}}_{pi}-\dot {\bar{\pmb x}}_{pj} ) }} \\ \end{array} }} \right], \end{align} $ | (27) |
the estimated joint-space reference acceleration as
| $ \begin{align} \hat {\ddot {\pmb q}}_{ri} = \bar J_i^{-1} (\hat {\ddot {\bar {\pmb x}}}_{ri}-\dot {\bar J}_i\hat {\dot {\pmb q}}_{ri}), \end{align} $ | (28) |
and the dynamic regressor matrix $Y_{di}$ as
| $ \begin{align} \hat {M_i}(\pmb q_i)\hat {\ddot {\pmb q}}_{ri} + \hat {C_i}(\pmb q_i,\dot {\pmb q}_i)\hat {\dot {\pmb q}}_{ri} + \hat {\pmb g}_i(\pmb q_i) = Y_{di} (\pmb q_i,\dot {\pmb q}_i,\hat {\dot {\pmb q}}_{ri} ,\hat {\ddot {\pmb q}}_{ri} )\hat {\pmb a}_{di}, \end{align} $ |
where $\hat {\dot {\bar {\pmb x}}}_{ri}$ and $\dot f_{ri}$ are given in (13) and (20),respectively.
Then,we propose the following adaptive control law
| $ \begin{align} &\pmb{\tau}_i =-\bar {J}^{\rm T}_i K_i\hat {\pmb s}_{\bar xi} + \bar J^{\rm T}_i\left[{{\begin{array}{*{20}c} f_i \\ 0_2 \\ \end{array} }} \right] + Y_{di} (\pmb q_i,\dot {\pmb q}_i,\hat {\dot {\pmb q}}_{ri} , \hat {\ddot {\pmb q}}_{ri} )\hat {\pmb a}_{di},\\\end{align} $ | (29) |
| $ \begin{align} & \dot {\hat {\pmb a}}_{di} =-\Gamma _{di} Y^{\rm T}_{di} (\pmb q_i,\dot {\pmb q}_i,\hat {\dot {\pmb q}}_{ri} ,\hat {\ddot {\pmb q}}_{ri} )\hat {\pmb s}_i, \end{align} $ | (30) |
where $K_i$ and $\Gamma _{di}$ are the adjustable positive definite matrices.
Now,for the overall system constituted by kinematic loop and dynamic loop,we present the following theorem.
Theorem 2. Consider the multiple robotic manipulator systems described by (3)$\sim$(5) with uncertain dynamic parameter $\pmb a_{di}$,environment stiffness $k_{si}$ and distance $\theta_{1i}$. Suppose Assumptions 1$\sim$3 and Condition 1 are satisfied. Then,the controller (29),the observer (16),and the updating laws (15) and (30) give rise to $\Delta f_i \to 0$, ${\Delta \dot {f}}_i \to 0$,${\Delta \bar {\pmb x}}_{pi} \to 0$, and ${\Delta \dot {\bar {\pmb x}}}_{pi} \to 0$ as $t \to \infty$,%where the estimated joint-space reference velocity $\hat {\dot {\pmb q}}_{ri}$ and the estimated joint-space reference acceleration $\hat {\ddot {\pmb q}}_{ri}$ are given in (12) and (28),respectively,the estimated task-space reference velocity $\hat {\dot {\bar {\pmb x}}}_{ri}$ and the estimated task-space reference acceleration $\hat {\ddot {\bar {\pmb x}}}_{ri}$ are given in (13) and (27),respectively. $\hat{v}_{fi}$,$\hat{\pmb v}_{pi}$,$\hat{a}_{fi}$ and $\hat{\pmb a}_{pi}$ are given in (8)$-$(11),respectively,$\hat {\pmb s}_{\bar xi}$ and $\hat {\pmb s}_i$ are given in (18) and (19),respectively,and $f_{di}$ and $\bar{\pmb x}_{pdi}$ are given in (6) and (7),respectively, $\forall i\in \mathcal {V}_F$.
Proof. We first substitute (29) into (4) to get the closed loop dynamics
| $ \begin{align} M_i\hat {\dot {\pmb s}}_i + C_i\hat {\pmb s}_i =-\bar {J}^{\rm T}_i K_i\hat {\pmb s}_{\bar xi} + Y_{di} (\pmb q_i,\dot {\pmb q}_i,\hat {\dot {\pmb q}}_{ri} ,\hat {\ddot {\pmb q}}_{ri} )\tilde {\pmb a}_{di}, \end{align} $ | (31) |
where $\hat {\dot {\pmb s}}_i=\ddot {\pmb q}_i-\hat{\ddot {\pmb q}}_{ri} $. Since Condition 1 gives rise to $\| {\hat {v}_{fi}- \dot {f}_{di} } \| \to 0$ and $\left\| {\hat {\pmb v}_{pi}-\dot {\bar {\pmb x}}_{pdi} } \right\| \to 0$,$\| {\hat {a}_{fi}-\ddot {f}_{di} } \| \to 0$ and $\left\| {\hat {\pmb a}_{pi}-\ddot {\bar {\pmb x}}_{pdi} } \right\| \to 0$ in finite time ${T_0}$[7],we also provide our proof in two parts separated by $T_0$ as the proof in Theorem 1. In the first part where $t\in [0,T_0]$,we should prove that for bounded initial values $\pmb q_i(0)$,$\dot {\pmb q}_i(0)$,$\hat {\pmb a}_{di}(0)$,$\hat {\theta }_{0i} (0)$,$\hat v_{fi}(0)$,$\hat {\pmb v}_{pi}(0)$,$\hat a_{fi}(0)$ and $\hat {\pmb a}_{pi}(0)$,$\pmb q_i$ and $\dot {\pmb q}_i$ will remain bounded. From (8)$\sim$(11),the boundedness of $\hat {v}_{fi}$, $\hat {\pmb v}_{pi}$,$\hat {a}_{fi} $ and $\hat {\pmb a}_{pi}$ are ensured. For bounded $\pmb q_i$ and $\dot {\pmb q}_i$,we can get bounded $\bar {\pmb x}_i$,$\dot {\bar {\pmb x}}_i$ and $\dot {\bar J}_i$,implying the boundedness of $f_i$,$\dot f_i$,$\bar {\pmb x}_{pi}$ and $\dot {\bar {\pmb x}}_{pi}$. In Section III-A,we have proved $f_{oi}-f_i\in \mathcal L_2\cap \mathcal L_\infty$ and $\hat \theta_{0i}\in \mathcal L_\infty$. Therefore,$\hat {\dot {\bar {\pmb x}}}_{ri}\in \mathcal L_\infty$ from (13),further indicating the boundedness of $\hat {\dot {\pmb q}}_{ri}$ in (12). Then,$\hat {\pmb s}_i \in \mathcal L_\infty$ and $\hat {\pmb s}_{\bar xi}\in \mathcal L_\infty$ are obtained. On the basis of (16),we get $\dot f_{oi}\in \mathcal L_\infty$ and $\dot {\hat \theta}_{0i}\in \mathcal L_\infty$. According to (27),we derive $\hat {\ddot {\bar {\pmb x}}}_{ri} \in \mathcal L_\infty$,further implying that $\hat {\ddot {\pmb q}}_{ri} \in \mathcal L_\infty$ based on (28). Then, from (30),$\dot {\hat {\pmb a}}_{di}$ is bounded,which implies the boundedness of $\hat {\pmb a}_{di}$. Therefore,we can get from (31) that $\hat{\dot {\pmb s}}_i \in \mathcal L_\infty$,resulting in the boundedness of $\ddot {\pmb q}_i$. Now we conclude that for bounded $ {\pmb q}_i(0)$,$\dot {\pmb q}_i(0)$,$\hat {\pmb a}_{di}(0)$, $\hat {\theta }_0 (0)$,$\hat v_{fi}(0)$,$\hat {\pmb v}_{pi}(0)$, $\hat a_{fi}(0)$ and $\hat {\pmb a}_{pi}(0)$,$\pmb q_i$,$\dot {\pmb q}_i$ and $\hat {\pmb s}_{\bar xi}$ remain bounded in finite time $T_0$.
Now,we proceed our proof for the second part where $t\in (T_0, \infty)$. Since the sliding mode estimators (8)$\sim$(11) converge in this period,by simple computation,we have $ \frac{\rm d} {{\rm d}t} \hat{\dot{\bar{\pmb x}}}_{ri} =\hat{\ddot{{\bar{\pmb x}}}}_{ri} $,and then,$\frac {\rm d}{{\rm d}t}\hat{\dot {\pmb q}}_{ri}=\hat{\ddot {\pmb q}}_{ri}$ and $\frac {\rm d}{{\rm d}t}\hat {\pmb s}_i=\hat{\dot {\pmb s}}_i$ can be derived. Therefore,for $t>T_0$,(31) can be rewritten as
| $ \begin{align} M_i \frac {\rm d}{{\rm d}t}\hat {\pmb s}_i + C_i\hat {\pmb s}_i =-\bar {J}^{\rm T}_i K_i\hat { {\pmb s}}_{\bar xi} + Y_{di} \left( \pmb q_i,\dot{\pmb q}_i,\hat {\dot {\pmb q}}_{ri} ,\frac {\rm d}{{\rm d}t}\hat{\dot {\pmb q}}_{ri} \right )\tilde {\pmb a}_{di}. \end{align} $ | (32) |
Let us take the Lyapunov-like function as
| $ \begin{align} V_{di} = \frac{1}{2}\hat {\pmb s}_i^{\rm T}M_i\hat {\pmb s}_i + \frac{1}{2}\tilde {\pmb a}_{di} ^{\rm T}\Gamma _{di}^{-1} \tilde {\pmb a}_{di}. \end{align} $ |
We differentiate $V_{di}$ with respect to time and substitute (30) into it. Due to the skew symmetry property of $\dot {M}_i-2C_i$,we have
| $ \begin{align} &\dot {V}_{di} = \hat{\pmb s}^{\rm T}_i \left(M_i\frac {\rm d}{{\rm d}t}\hat {\pmb s}_i + C_i \hat {\pmb s}_i \right) + \tilde {\pmb a}^{\rm T}_{di} \Gamma _{di}^{-1} \dot {\hat {\pmb a}}_{di}= \\ &\qquad-\hat {\pmb s}_{\bar xi}^{\rm T} K_i\hat {\pmb s}_{\bar xi}\le 0, \end{align} $ |
which implies that $\hat {\pmb s}_{\bar xi} \in \mathcal L_2$, $\hat {\pmb s}_i \in \mathcal L_\infty $ and $\tilde {\pmb a}_{di}\in \mathcal L_\infty$,and thus $\hat {\pmb s}_{\bar xi}\in \mathcal L_\infty$. Then,Condition 2 in Theorem 1 holds. By Assumptions 2 and 3,Conditions 1 and 2,we can derive that $\Delta {\bar {\pmb x}}_i \in \mathcal L_2\cap \mathcal L_\infty $,$\hat {\theta}_{0i} \in \mathcal L_\infty $,$\dot {\hat \theta}_{0i}\in \mathcal L_\infty$,$\dot {f}_{oi} \in \mathcal L_\infty $,$\dot {\bar {\pmb x}}_{pi} \in \mathcal L_\infty $, and $\Delta {\bar {\pmb x}_i} \to 0$,as $t \to \infty $ from Theorem 1,yielding $\hat {\ddot {\bar {\pmb x}}}_{ri} \in \mathcal L_\infty$ from (27). Meanwhile,we have $\hat {\dot {\pmb q}}_{ri}\in \mathcal L_\infty$ and $\dot {\pmb q}_i=\hat {\pmb s}_i+\hat {\dot {\pmb q}}_{ri}\in \mathcal L_\infty$,leading to the boundedness of $\dot {\bar J}_i$. Then,based on (28),we get $\frac {\rm d}{{\rm d}t} \hat{\dot {\pmb q}}_{ri} \in \mathcal L_\infty$. Therefore,$\frac {\rm d}{{\rm d}t}{\hat {\pmb s}}_i \in \mathcal L_\infty$ can be derived from (32),which implies the boundedness of $\ddot {\pmb q}_i$,and then the boundedness of $\Delta \ddot {\bar {\pmb x}}_i$. Because of the fact that $\Delta {\bar {\pmb x}}_i \in \mathcal L_2\cap \mathcal L_\infty$ and the uniform continuity of $\Delta \dot {\bar {\pmb x}}_i$,we get that $\Delta \dot {\bar {\pmb x}}_i\to 0$ as $t \to \infty$ from Lemma 3. Combining with Theorem 1,we obtain that $\Delta {f}_i \to 0$, $\Delta {\dot {f}}_i \to 0$,$\Delta {\bar {\pmb x}}_{pi} \to 0$ and $\Delta {\dot {\bar {\pmb x}}}_{pi} \to 0$ as $t\to\infty$.
Remark 2. In Theorem 2,the uncertain distance $\theta_{1i}$ is compensated via the stiffness adaptation (15) and the force observer (16). In fact,in the definition of estimated task-space reference velocity (13),the construction of the force observer enables us to utilize $\hat \theta_{0i} f_{oi}$ as the estimated deformation in the surface normal direction. From (2),we can get the expression of the estimated distance $\theta_{1i}$ as ${\pmb x}_i^{\rm T} {\pmb n}_{si}-\hat{\theta}_{0i}f_{oi}$. Yet,the variable $\hat {\theta}_{1i}$ is not utilized in our design
.Remark 3. The overall system can be decomposed as a cascade of two subsystems,i.e.,(21) and (31). The former is the kinematic loop with states $\left[{{\begin{array}{*{20}c} \hat {\theta }_{0i} \Delta {f}_{oi} & \Delta {\bar {\pmb x}}_{pi}^{\rm T} \\ \end{array} }} \right]^{\rm T}$ and the latter is the dynamic loop with states $(\hat {\pmb s}_i$,$\tilde {\pmb a}_{di})$. The dynamic loop is an extension of the Slotine and Li controller[20].
Ⅳ.SIMULATIONIn this section,we use six two-link planar robotic manipulators to validate our control algorithm. For the $i$th manipulator, physical parameters of the two links are selected as
| $ \begin{align*} &m_{i}^1=1+0.3i,\quad l_{Ci}^1=0.1+0.03i,\quad r_{i}^1=0.1+0.03i,\\ &m_{i}^2=1.5+0.3i,\quad l_{Ci}^2=0.15+0.03i,\quad r_{i}^2=0.15+0.03i, \end{align*} $ |
where $m_{i}^{\bar i}$ is the mass of the $\bar i$th link, $l_{Ci}^{\bar i}$ is the position of the mass center, $l_{Ci}^{\bar i}+r_{i}^{\bar i}$ is the length of the $\bar i$th link,and the moment of inertia relative to the mass center can be calculated as $I_{i}^{\bar i}=\frac {1}{12}m_{i}^1(l_{Ci}^{\bar i}+r_{i}^{\bar i})^2$,$\bar i \in\{1,2\}$,$i\in \{1,\cdots,6\}$.
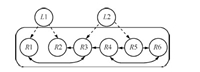
We assume that there are two leaders. The information graph associated with the leaders and the followers is shown in Fig. 2, where $L1$ and $L2$ denote the two virtual leaders and $R1$,$\cdots$, $R6$ denote the six robotic followers. We choose $w_{ij} =1$ if $(j$,$i) \in \mathcal {E}$,and $w_{ij} = 0$ otherwise,$i$, $j\in \{1,\cdots,8\}$. The leaders$'$ force and position trajectories are $f_{Lk} = \mbox{(20 + 20$\cos$(0.1$t$))}k$ and $\bar x_{pLk} =\mbox{ 0.1$k$ $\sin$ (0.1$t$)}$,$k\in \{1,2\}$, respectively.
|
Download:
|
| Fig. 2 Interaction graph of the agents. | |
For simplicity,the gravitational force is neglected and the transformation matrix $R_i$ is assumed to be identity matrix in our simulation. In addition,the stiffness of the environment and the distance from the base to the surface are assumed to be $k_{si}=1000$ and $\theta_{1i}=0.55$,respectively. The initial joint position and initial velocity of the manipulator are set as $\pmb q_i(0)=\left[{{\begin{array}{*{20}c} \frac{1}{18} (i+1)\pi &-\frac{1}{36}(i+1) \pi \\ \end{array} }} \right]^{\rm T}$ and $\dot {\pmb q}_i(0) = \left[ {{\begin{array}{*{20}c} 0.05i-0.2 &-0.05i+0.2 \\ \end{array} }} \right]^{\rm T} $,respectively. The observer gains are selected as $\Lambda_{oi}=10$, $\beta_{f1}=10,\beta_{p1}=10,\beta_{f2}=10$ and $\beta_{p2}=10$. The gains for the controller and updating laws are chosen as ${\Lambda_i }= {\rm diag}\{2,\quad 10\}, K_i=100\times{\rm diag}\{2,\quad 1\},\Gamma_{0i}=5e-8$ and $\Gamma_{di}=0.001{I}_3$. The sampling period is selected as $T_s=0.002 {\rm s}$.
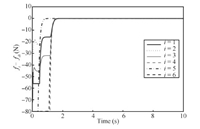
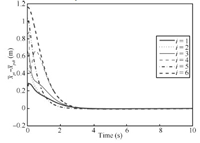
Fig. 3 illustrates the transients of force tracking errors. The end-effectors of the robots are not in contact with the environment in the initial period,so the contact force remains zero during the early period until the end-effector touches the surface. Fig. 4 shows the transients of position tracking errors. The force and position of all robotic agents asymptotically converge to the desired values,i.e.,the convex hull formed by the leaders. Fig. 5 shows converging process of the force observation errors. The adaptation of $\hat \theta_{0i}$ begins when the $i$th robotic agent interacts with the environment,as illustrated in Fig. 6.
|
Download:
|
| Fig. 3 Force tracking errors of the agents. | |
|
Download:
|
| Fig. 4 Position tracking errors of the agents. | |

|
Download:
|
| Fig. 5 Observation errors of the force observers. | |

|
Download:
|
| Fig. 6 The updating process of $ \hat {\theta}_{0i}$. | |
In this paper,we consider force/position consensus tracking of multiple robotic manipulators under directed graphs,where the end-effectors of the robots are in contact with flat compliant surfaces with uncertain stiffness and distance. We propose a distributed adaptive hybrid controller to realize both force and task-space position tracking to the convex hull spanned by the leaders. A novel decentralized force observer is constructed to achieve consensus tracking in the force direction with environment uncertainties,which also helps to get rid of the reliance on the measurements of force derivatives. A decentralized stiffness estimator is constructed to estimate environment parameters online. Our scheme removes the requirement for the estimation of surface distance,and offers a simple and direct solution to force synchronization problem in a cascaded framework. Simulations are also performed to examine effectiveness of the proposed strategy. Our future work will focus on investigating the feasibility of extending our strategy to the case when the surface-orientation uncertainties as well as the robotic kinematic and dynamic uncertainties are involved.
| [1] | Jones C V, Mataric M J. Behavior-based coordination in multi-robot systems. Autonomous Mobile Robots:Sensing, Control, Decision-Making and Applications. United States:Marcel Dekker, Inc., 2005 |
| [2] | Bullo F, Cortes J, Martinez S. Distributed Control of Robotic Networks. Princeton:Princeton University Press, 2009 |
| [3] | Ren W. Distributed leaderless consensus algorithms for networked Euler-Lagrange systems. International Journal of Control, 2009, 82(11):2137-2149 |
| [4] | Chopra N, Spong M W, Lozano R. Synchronization of bilateral teleoperators with time delay. Automatica, 2008, 44(8):2142-2148 |
| [5] | Sun D, Shao X Y, Feng G. A model-free cross-coupled control for position synchronization of multi-axis motions:theory and experiments. IEEE Transactions on Control Systems and Technology, 2007, 15(2):306-314 |
| [6] | Nuno E, Ortega R, Basanez L, Hill D. Synchronization of networks of nonidentical Euler-Lagrange systems with uncertain parameters and communication delays. IEEE Transactions on Automatic Control, 2011, 56(4):935-941 |
| [7] | Cao Y, Ren W, Meng Z. Decentralized finite-time sliding mode estimators and their applications in decentralized finite-time formation tracking. Systems & Control Letters, 2010, 59(9):522-529 |
| [8] | Mei J, Ren W, Ma G. Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph. Automatica, 2012, 48(4):653-659 |
| [9] | Wang H. Task-space synchronization of networked robotic systems with uncertain kinematics and dynamics. IEEE Transactions on Automatic Control, to be published |
| [10] | Wang L J, Meng B, Wang H T. Adaptive task-space synchronisation of networked robotic agents without task-space velocity measurements. International Journal of Control,DOI:10.1080/00207179.2013.835173 |
| [11] | Careli R, Kelly R, Ortega R. Adaptive force control of robot manipulators. International Journal of Control, 1990, 52(1):37-54 |
| [12] | Chiaverini S, Siciliano B, Villani L. Force and position tracking:parallel control with stiffness adaptation. IEEE Control Systems Magazine, 1998, 18(1):37-54 |
| [13] | Villani L, de Wit C C, Brogliato B. An exponentially stable adaptive control for force and position tracking of robot manipulators. IEEE Transactions on Automatic Control, 1999, 44(4):798-802 |
| [14] | Doulgeri Z, Karayiannidis Y. Force/position tracking of a robot in compliant contact with unknown stiffness and surface kinematics. In:Proceedings of IEEE International Conference on Robotics and Automation. Roma, Italy:IEEE, 2007.4190-4195 |
| [15] | Li Z, Li J, Kang Y. Adaptive robust coordinated control of multiple mobile manipulators interacting with rigid environment. Automatica, 2010, 46(12):2028-2034 |
| [16] | Cortesao R, Coutinho F. Environment stiffness estimation with multiple observers. In:Proceedings of IEEE 35th Annual Conference on Industrial Electronics. Porto, Portugal:IEEE, 2009. 1537-1542 |
| [17] | Craig J J. Introduction to Robotics:Mechanics and Control. Upper Saddle River, NJ:Prentice Hall, 2005. 135-139 |
| [18] | Kelly R, Santibanez V, Loria A. Control of Robot Manipulators in Joint Space. London:Springer, 2005.113-116 |
| [19] | Lozano R, Brogliato B, Egeland O, Maschke B. Dissipative Systems Analysis and Control. London:Springer-Verlag, 2000.182-186 |
| [20] | Slotine J J E, Li W. Applied Nonlinear Control. Englewood Cliffs, NJ:Prentice Hall, 1991.397-409 |
 2014, Vol.1
2014, Vol.1 


