2. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210003, China;
3. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210003, China;
4. College of Automation, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
MULTI-AGENT systems have received considerable attention in recent years with the great development of computer science,communication,computation and control. Compared with single system,multi-agent system not only provides robustness to failures and uncertainties,but also gives us some flexibilities to control or reconfigure the whole system. Furthermore,the performance has been greatly leveraged when using multi-agent system in cooperative surveillance and monitoring,cooperative navigation or cooperative movement. Advantages of using multi-agent system have been shown in unmanned aerial vehicles (UAVs),unmanned underwater vehicles (UUVs),unmanned ground vehicles (UGVs),spacecraft formation flight,etc.
Research related to consensus can date back to the work of [1]. Recent years have seen a lot of works related to this topic. Consensus protocols for single integrator systems have been given in [2, 3, 4, 5, 6] to name a few. While consensus of double integrator systems are considered in [7, 8, 9]. The consensus problem of linear systems with high order or nonlinear systems is much more challenging compared with that of the integrator systems. For linear time invariant system,a lot of work has adopted the philosophy of "decomposition" to reduce complexity as shown in the following. Cooperative control of multiple linear time-invariant (LTI) vehicles has been realized in [5] using the technique of Schur decomposition. Based on this decomposition,the cooperative control problems of multiple LTI systems have been transformed into control problems of multiple simple subsystems. Then the cooperative control problems of the original system will be solved if each subsystem is stabilized as shown in [10] and [11]. Some other results such as $H_{\infty}$ and $H_{2}$ stability for multiple continuous LTI systems are also obtained in [12] and [13] using the framework of "decomposition".
In order to solve the cooperative control problem of multiple nonlinear dynamic systems,nonlinear tools and system structure have been introduced in some recent papers. Tools from dissipative theory have been adopted in [14] to characterize the constraints on communication channels in the distributed control of dynamic system. Other nonlinear tools,such as input to state stability (ISS) in [15] and [16],internal mode control in [17] and passivity in [18] and [19],are also introduced into the cooperative control of multiple nonlinear dynamic systems. Cascaded system theories are used in [20] for the attitude synchronization problem of spacecrafts with disturbance. Similar results also can be found in [21] for synchronization of multiple chaotic systems.
A. Distributed Control of Multiple Nonholonomic SystemsCompared with linear systems or normal nonlinear systems,control of multiple nonholonomic systems is much more difficult. As shown in [22],there are no smooth (or even continuous) time-invariant state feedback controllers to asymptotically stabilize this kind of system. Controllers for linear systems or normal nonlinear systems are not effective any more when applied to nonholonomic systems.
Some previous work on cooperative control of nonholonomic systems have only considered the cooperative control problem under persistent reference signals. The nonholonomic robots are required to keep rotating or oscillating in [23] for the cooperative hunting problem. The direction angles are left to oscillate sinusoidally in [24] for the formation control problem,and the reference target's velocities are not allowed to converge to zero in [25] and [19] for the cooperative path-following control problem. In circular motion control problem,the assumption of rotating around a virtual beacon is imposed in [26] for nonholonomic robots. Similarly,linear velocity of the leader robot is not allowed to be equal to zero in [27, 28, 29] to guarantee controllability of the nonholonomic unicycles.
The stabilization and tracking control problems of single nonholonomic systems have received a lot of attention due to the challenges presented in control of this kind of systems. There are many papers about designing controllers for this kind of systems using time-varying,discontinuous or hybrid feedback controllers. It is worthy of considering whether Brockett's condition is also effective in the cooperative control of multiple nonholonomic systems. Consensus for networked nonholonomic unicycles has been realized using time invariant continuous feedback controllers in [30] without group reference. Results obtained in [30] have shown that Brockett's condition is not a barrier in consensus of nonholonomic unicycles. Different from the work of [30] where the consensus value cannot be specified,the consensus problem of networked multiple nonholonomic mobile robots with groups reference trajectory will be considered in this paper.
B. Main Contributions of This PaperConsensus of multiple nonholonomic mobile robots with group reference has been considered in this paper. Consensus protocols have been constructed no matter the reference signal converges to zero or not,so that consensus on different kinds of reference signals can be realized using controllers of this paper. Cascaded theories of nonautonomous system have been introduced to transform the consensus problem of one complex system into consensus problems of two simple subsystems. Some persistent exciting signals have been injected to realize consensus of all state variables. To our best knowledge,there are few papers considering the consensus problem of multiple nonholonomic systems when the group reference signals converge to zero.
The rest of the paper is organized as follows. System model and problem statements are firstly given in Section Ⅱ. Some preliminary results are also included in Section Ⅱ. Challenges in control of nonholonomic systems are discussed in Section Ⅲ,and one simulation is included to show that previous consensus protocols cannot be directly extended to the consensus problem of nonholonomic mobile robots. Consensus protocols and our main theorems are proposed in Section Ⅳ. Simulation results and conclusions are given in Section V and Section Ⅵ,respectively.
Ⅱ. PRELIMINARIESFor $N$ nonholonomic mobile robots (indexed by $1,2,\cdots,N$) that move on a plane,we assume that each of them has the same mechanical structure and can be described by the following equations in the global coordinate frame:
| \begin{align} &\dot{x}_{i}=u_{i}\cos\theta_{i}\notag,\nonumber\\ &\dot{y}_{i}=u_{i}\sin\theta_{i},\nonumber\\ &\dot{\theta}_{i}=\omega_{i}, \end{align} | (1) |
where $i=1,2,\cdots,N.$
The $N$ mobile robots can be represented by $N$ vertices of graph $G=(\mathcal{V},E)$,where $\mathcal{V}$ is the set of vertices, $E$ is the set of all edges where one edge $(j,i)\in E$ means the state of robot $j$ is available to robot $i$. For the graph $G$ with $N$ robots,the adjacency matrix $A=A(G)=(a_{ij})$ can be defined as $a_{ij}=1$ if there is one edge $(j,i)\in E$,and $a_{ij}=0$,otherwise. Let $N_{i}$ be the collection of neighbours for robot $i$,and the desired reference trajectory for the group can be described as the following system:
| \begin{align} &\dot{x}_{d}=u_{d}\cos\theta_{d}\notag,\nonumber\\ &\dot{y}_{d}=u_{d}\sin\theta_{d},\nonumber\\ &\dot{\theta}_{d}=\omega_{d}, \end{align} | (2) |
where $u_{d},\omega_{d}$ are known time-varying functions. Our control problem is defined as follows.
Consensus problem. Design a controller for each follower based on its neighbours and its own states such that the group of robots will reach consensus on the desired group reference,i.e., design control laws for systems (1) such that
| \begin{align} &\lim_{t\rightarrow\infty}\left(\begin{bmatrix}x_{i}-x_{j}\\y_{i}-y_{j}\end{bmatrix} \right)=0,\lim_{t\rightarrow\infty}\left(\begin{bmatrix}x_{i}-x_{d}\\y_{i}-y_{d}\end{bmatrix} \right)=0,\end{align} | (3) |
| \begin{align} &\lim_{t\rightarrow\infty}(\theta_{i}-\theta_{j})=0,\lim_{t\rightarrow\infty}(\theta_{i}-\theta_{d})=0, \end{align} | (4) |
where $i,j=1,2,\cdots,N$.
Practical consensus problem. Under appropriate controllers and communication topology,all the states of robot system (1) will converge to a domain of the desired value,i.e.,there exists a constant $\varepsilon>0$ and appropriate cooperative controllers for system (1) such that
| \begin{align} &\lim_{t\rightarrow\infty}\left(\begin{bmatrix}x_{i}-x_{j}\\y_{i}-y_{j}\end{bmatrix} \right)<\varepsilon,\lim_{t\rightarrow\infty}\left(\begin{bmatrix}x_{i}-x_{d}\\y_{i}-y_{d}\end{bmatrix} \right)<\varepsilon,\end{align} | (5) |
| \begin{align} &\lim_{t\rightarrow\infty}(\theta_{i}-\theta_{j})<\varepsilon,\lim_{t\rightarrow\infty}(\theta_{i}-\theta_{d})<\varepsilon, \end{align} | (6) |
where $i,j=1,2,\cdots,N$.
Now,we recall some definitions and lemmas that will be used in the next section.
Definition 1[31]. ${\pmb \omega_{d}}$ is persistently exciting,i.e.,there exist positive constants $\alpha_1, \alpha_2$ and $\delta$ such that the following condition holds for all $t>0$:
| \begin{align} \alpha_{1}{ I}\leq\int_{t}^{t+\delta}{\pmb \omega_{d}}(\tau){\pmb \omega_{d}}^{\rm T}(\tau) {\rm d}\tau\leq\alpha_{2}{I}. \nonumber \end{align} |
Lemma 1[32]. Consider a linear time-varying system in the form of
| \begin{align*} \dot{\pmb x}=({A_0}+{A_1(t)}){\pmb x}, \end{align*} |
where ${A_0}$ is a constant and Hurwitz matrix,${A_1(t)}$ is time-varying and satisfies
| \begin{align} A_1(t)\rightarrow 0\ {\rm as}\ t\rightarrow\infty,\ \ \ \int_{0}^{\infty}\|A_1(t)\|\,{\rm d}t<\infty. \nonumber \end{align} |
The systems is globally uniformly exponentially stable (GUES).
Lemma 2[31]. Consider a linear time-varying system
| \begin{align} \dot{\pmb x}=A(\phi(t)){\pmb x}+B{\pmb u}, \end{align} | (7) |
where $A(\phi)$ is continuous and $\phi: {\bf R} \to {\bf R}$ is continuous. We assume that for all $s\neq 0$ the pair $(A(s),B)$ is controllable. If $\phi(t)$ is bounded and Lipschitz,and there exist constants $\delta_{c}>0$ and $\epsilon >0$ such that
| \begin{align} \forall t \geq 0,\exists s: t-\delta_c\leq s\leq t \ {\rm such \ that} \ |\phi(s)| \geq \epsilon,\nonumber \end{align} |
then system (7) is uniformly completely controllable.
Consider a time-varying cascaded system $\dot{\pmb z}=f(t,{\pmb z})$ that can be written as[33]
| \begin{align} &\dot{\pmb z}_{1}=f_{1}(t,{\pmb z}_{1})+g(t,{\pmb z}_{1},{\pmb z}_{2}){\pmb z}_{2},\nonumber\\ &\dot{\pmb z}_{2}=f_{2}(t,{\pmb z}_{2}). \end{align} | (8) |
Actually,system (8) can be regarded as
| \begin{align} \Sigma_{1}:\;\;\;\dot{\pmb z}_{1}=f_{1}(t,{\pmb z}_{1}) \end{align} | (9) |
perturbed by the output of the system
| \begin{align} \Sigma_{2}:\;\;\;\dot{\pmb z}_{2}=f_{2}(t,{\pmb z}_{2}). \end{align} | (10) |
Lemma 3[31, 33]. The cascade time-varying system (8) is globally $\mathcal{K}$-exponentially stable if the following conditions are satisfied.
1) Subsystem (9) is globally uniformly exponentially stable.
2) The function $g(t,{\pmb z}_{1},{\pmb z}_{2})$ satisfies the following condition for all $t\geq t_{0}:$
| \begin{align} &g(t,{\pmb z}_{1},{\pmb z}_{2})\leq \theta_{1}(\|{\pmb z}_{2}\|)+\theta_{2}(\|{\pmb z}_{2}\|)\|{\pmb z}_{1}\|,\nonumber \end{align} |
where $\theta_{1}:{\bf R}^{+}\rightarrow {\bf R}^{+},\theta_{2}:{\bf R}^{+}\rightarrow {\bf R}^{+}$ are continuous functions.
3) Subsystem (10) is globally $\mathcal{K}$-exponentially stable.
Ⅲ. CHALLENGES IN CONTROL OF NONHOLONOMIC MOBILE ROBOTS A. Control of Single Nonholonomic Mobile RobotSystem (1) can also be rewritten as
| \begin{align} \left[\begin{array}{*{20}c}\dot{x}_{i}\\ \dot{y}_{i}\\ \dot{\theta}_{i} \end{array}\right] =\left[\begin{array}{*{20}c} \cos\theta_{i}\\ \sin\theta_{i}\\ 0 \end{array}\right]u_{i}+\left[\begin{array}{*{20}c} 0\\ 0\\ 1 \end{array}\right]\omega_{i}. \end{align} | (11) |
It is easy to prove that system (11) is controllable using the Lie algebra rank condition of [34]. However,it has been proved in [22] that a necessary condition for smoothly stabilizing a driftless regular system (i.e.,the input vector fields are linearly independent at the desired equilibrium) is that the number of inputs equals the number of states. The well-known result obtained in [22] is that there are no static smooth or even continuous stabilization controllers for the stabilization problems of system (1).
A lot of efforts have been put into the control of this kind of systems. For example,time-varying controllers,discontinuous controllers or even hybrid controllers have been proposed for stabilization problem or tracking control problem in recently published papers.
B. Control of Multiple Nonholonomic Mobile RobotsOne interesting question is whether Brockett's necessary condition is still a big challenge for the consensus problem of multiple nonholonomic system. Some preliminary work has been given in [30] that consensus of networked nonholonomic mobile robots can be obtained using linear time-invariant continuous state feedback. But it is still unknown what is the relationship between consensus value and initial states,and how to specify and achieve such consensus value is still open. The authors believe that achieving consensus on certain desired consensus value is much preferred in many applications,such as flocking and swarming problem of mobile robots,and rendezvous and docking problem of spacecraft systems. Thus,the consensus problem of networked multiple nonholonomic mobile robots with group reference trajectory will be considered in this paper.
As shown in [35],system (1) can be transformed into the following nominal chained form by input and state transformation:
| \begin{align} &\dot{x}_{i1} =u_{i1},\nonumber\\ &\dot{x}_{i2} =u_{i2},\nonumber\\ &\dot{x}_{i3} =u_{i1}x_{i2}. \end{align} | (12) |
Similarly,the group reference system (2) can also be transformed into
| \begin{align} &\dot{x}_{1}^{d} =u_{1}^{d},\nonumber\\ &\dot{x}_{2}^{d} =u_{2}^{d},\nonumber\\ &\dot{x}_{3}^{d} =u_{1}^{d}x_{2}^{d}. \end{align} | (13) |
If we apply the previous consensus protocols for the design of $u_{i1}$ as
| \begin{align} u_{i1}=-k_{0}a_{i0}(x_{i1}-x_{1}^{d})+\sum_{j\in N_{i}} a_{ij}(x_{j1}-x_{i1}), \end{align} | (14) |
where $a_{ij}=1$ means that the state information of agent $j$ can be obtained by agent $i$,and $a_{i0}=1$ means that the state information of the reference agent can be obtained by agent $i$, otherwise,$a_{ij}=0$ and $a_{i0}=0$ means there is no communication between them.
Under the following cooperative controller
| \begin{align} &u_{i2}=-k_{2}\!\!\sum_{j\in N_{i},j\neq i}a_{ij}(x_{i2}-x_{j2})-\nonumber\\ &\qquad k_{3}u_{i1}\sum_{j\in N_{i},j\neq i}a_{ij}(x_{i3}-x_{j3}),\nonumber \end{align} |
we first consider the consensus problem when the communication topology is undirected and connected under the assumption that the reference input converges to zero,i.e.,$u_{1d}=\exp(-t)$.
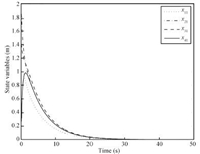
Matlab simulation using the above controllers have been conducted for four nonholonomic mobile robots. Simulation results given in Figs. 1 and 2 show that consensus of state $x_{i1}$ and $x_{i2}$ has been obtained using the above consensus protocols while consensus of the third state cannot be reached as shown in Figs. 3 and 4. The failure of third state's consensus can be concluded from uncontrollability of subsystem $x_{i3}$ of (12) when $u_{i1}$ reaches consensus on signal converging to zero.
|
Download:
|
| Fig. 1. Consensus of $x_{i1}$ ($i = 1,2, 3,4$). | |

|
Download:
|
| Fig. 2. Consensus of $x_{i2}$ ($i = 1,2,3,4$). | |

|
Download:
|
| Fig. 3. Consensus of $x_{i3}$ ($i = 1,2,3, 4$). | |
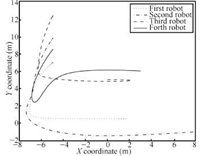
From the above simulation results,it is easy to see that only partial consensus (consensus of direction angels and consensus of $x$ coordinate) can be obtained in this case. So the previous results on consensus of integrator systems or linear systems cannot be directly extended to the consensus of nonholonomic mobile robots.
|
Download:
|
| Fig. 4. Trajectories of each nonholonomic robot. | |
Due to the challenges presented in the previous section,different consensus protocols will be considered when $u_{1}^{d}$ is persistent exciting signal and when $u_{1}^{d}\rightarrow0$ (even $u_{1}^{d}=0$),respectively.
1) When $u_{1}^{d}$ is persistent exciting signal
As all the states of (12) are controllable in this case,the consensus problem of (12) is not too difficult. Controller (14) is still adopted to deal with consensus of the first subsystem of (12).
Remark 1. It is easy to see that in this case the consensus protocols for the first subsystem of (12) are not different from that of integrator systems obtained in [2, 3, 4, 5].
2) When $u_{1}^{d}\rightarrow0$ (or even $u_{1}^{d}=0$)
First,let $\rho_{i}=\sum_{j\in N_{i}}\sqrt{(x_{j2}-x_{i2})^{2}+(x_{j3}-x_{i3})^{2}}$ be the average distance between system $i$ and its neighbours.
Controller $u_{i1}$ are constructed as
| \begin{align}u_{i1}\!\!=\!\!\left\{\begin{aligned} \!\!\!&-\!\!k_{0}a_{i0}(x_{i1}\!\!-\!\!x_{1}^{d})\!+\!\!\! \sum_{j\in N_{i}}\!\!\! a_{ij}(x_{j1}\!\!-\!\!x_{i1})\!\!+\!\!k\sin(t),\!\!&{\rm if}\,\rho_{i}\geq \varepsilon,\\ \!\!\!&-\!\!k_{0}a_{i0}(x_{i1}\!\!-\!\!x_{1}^{d})\!+\!\!\!\sum_{j\in N_{i}}\!\!\! a_{ij}(x_{j1}\!\!-\!\!x_{i1}),&\!\!{\rm if}\,\rho_{i}< \varepsilon, \end{aligned}\right.\label{ui2}\end{align} | (15) |
where $k\neq0$ is the level of perturbation and $\varepsilon$ is the desired error range of $\rho_{i}$.
Remark 2. Concerning the controller design of $u_{i1}$ in this case,we have the following comments.
1) To our knowledge,this work reports the first consensus results of nonholonomic mobile robots with $u_{1}^{d}\rightarrow0$ (or even $u_{1}^{d}=0$).
2) The philosophy in the design of $u_{i1}$ in this case is to add some perturbing signals,such as persistent sinusoidal signal in $u_{i1}$,to guarantee controllability of the entire system.
3) The desired error range $\varepsilon$ can be as small as possible to satisfy some desired requirements in application.
4) The controller design of $u_{i1}$ in this case is discontinuous,and the continuous version of $u_{i1}$ is
| \begin{align*}u_{i1}= -k_{0}a_{i0}(x_{i1}\!\!-\!\!x_{1}^{d})\!+\!\!\sum_{j\in N_{i}}\!\! a_{ij}(x_{j1}\!\!-\!\!x_{i1})+k\sin(t)\rho_{i}. \end{align*} |
1) Controller design of $\pmb{u_{i2}}$} Let ${\pmb Z}_{2}=[x_{22},x_{32},\cdots,x_{N2}]^{\rm T}$ and ${\pmb Z}_{3}=[x_{23},x_{33},\cdots,$\\ $x_{N3}]^{\rm T}.$ Based on the previous research on control of nonholonomic mobile robots[36],the following controller
| \begin{align} {\pmb u}_{i2}=-k_{2}L{\pmb Z}_{2}-k_{3}u_{i1}L{\pmb Z}_{3} \end{align} | (16) |
is introduced no matter $u_{i1}$ converges to persistent exciting signal or zero,where $k_{2}>0$ and $k_{3}>0$ are constants,and $L\in {\bf R}^{n\times n}$ is Laplacian matrix of undirected connected graph.
Remark 3. From the structure of (16),it is easy to see that consensus of $x_{i3}$ will not be obtained when $u_{1}^{d}\rightarrow0$ (or $u_{1}^{d}=0$) if $u_{i1}$ of all robots reach consensus faster than consensus of ${\pmb Z}_{2}$ and ${\pmb Z}_{3}$. Thanks to the persistent excitation introduced in $u_{i1}$ as shown in the previous section,consensus of all state variables can still be reached using the proposed control strategy (16).
B. Main TheoremsTheorem 1. The system
| \begin{align} \left[\begin{array}{*{20}c} \dot{\pmb Z}_{2}\\ \dot{\pmb Z}_{3} \end{array}\right]=\left[\begin{array}{*{20}c} -k_{2}L&-k_{3}\phi(t)L\\ \phi(t)I_{N}&0 \end{array}\right]\left[\begin{array}{*{20}c} {\pmb Z}_{2}\\ {\pmb Z}_{3} \end{array}\right] \end{align} | (17) |
will reach consensus exponentially if $\phi(t)$ is persistently exciting,where $k_{2}>0$,$k_{3}>0$ are constants,and $L\in {\bf R}^{n\times n}$ is Laplacian matrix of connected graph.
Proof. Consider Laplacian potential function associated with the undirected graph $G$ as
| \begin{align} V=\frac{k_{2}}{2}{\pmb Z}^{\rm T}_{2}L^{\rm T}{\pmb Z}_{2}+\frac{k_{2}k_{3}}{2}{\pmb Z}^{\rm T}_{3}L^{\rm T}L{\pmb Z}_{3}, \end{align} | (18) |
which is positive semi-definite when $G$ is connected. It is easy to obtain that
| \begin{align*} \dot{V}=~&k_{2}{\pmb Z}^{\rm T}_{2}L^{\rm T}(-k_{2}L{\pmb Z}_{2}-k_{3}\phi(t)L{\pmb Z}_{3})+\\ &k_{2}k_{3}\phi(t){\pmb Z}_{3}^{\rm T}L^{\rm T}L{\pmb Z}_{2}=-k^{2}_{2}{\pmb Z}^{\rm T}_{2}L^{\rm T}L{\pmb Z}_{2}\leq 0, \end{align*} |
which is negative semi-definite.
From $\dot{V}=0$,we can obtain that
| $$L{\pmb Z}_{2}=0.$$ |
As shown in (17),we have $L\dot{\pmb Z}_{2}=-k_{2}L{\pmb Z}_{2}-k_{3}\phi(t)L{\pmb Z}_{3}$. Then $L{\pmb Z}_{3}=0$ can be easily obtained,since $\phi(t)$ is persistent exciting signal. Then the biggest invariant set of $\dot{V}=0$ is
| $$\left\{[{\pmb Z}_{2},{\pmb Z}_{3}]^{\rm T}|L{\pmb Z}_{2}=0,L{\pmb Z}_{3}=0\right\}.$$ |
Application of LaSalles invariant principle shows that $[{\pmb Z}_{2},{\pmb Z}_{3}]^{\rm T}$ will converge to $\dot{V}=0$ exponentially,which means consensus of $x_{12},x_{22},\cdots,x_{N2}$ and $x_{13},x_{23},\cdots,x_{N3}$ will be exponentially reached if $L\in {\bf R}^{n\times n}$ is Laplacian matrix of connected graph.
Theorem 2. Consensus when $\pmb{u_{1}^{d}}$ is persistent exciting signal.
The consensus problem of system (1) can be solved using controllers (14) and (16),when the communication topology is connected and at least one system accesses the information of $x_{1}^{d}$.
Proof. Under controllers (14) and (16),the closed loop system can be written as
| \begin{align} &\left[\begin{array}{*{20}c}\dot{\pmb Z}_{2}\\\dot{\pmb Z}_{3}\end{array}\right]=\left[\begin{array}{*{20}c} -k_{2}L&-k_{3}\Lambda_{u_{i1}}L\\ \Lambda_{u_{i1}}&0 \end{array}\right]\left[\begin{array}{*{20}c}{\pmb Z}_{2}\\{\pmb Z}_{3}\end{array}\right], \end{align} | (19) |
| \begin{align} &\dot{\pmb Z}_{1}=-k_{0}\Lambda_{a_{i0}}({\pmb Z}_{1}-{\pmb Z}_{1}^{d})+L{\pmb Z}_{1}, \end{align} | (20) |
where ${\pmb Z}_{1}=[x_{11},x_{21},\cdots,x_{N1}]^{\rm T}$,\quad ${\pmb Z}_{1}^{d}=[x_{1}^{d},x_{1}^{d},\cdots,x_{1}^{d}]^{\rm T}$,\\ $\Lambda_{u_{i1}}={\rm diag}\{u_{11},u_{21},\cdots,u_{N1}\}$,and $\Lambda_{a_{i0}}={\rm diag} \{a_{10},a_{20},\\\cdots,a_{N0}\}$.
If we substitute $u_{i1}$ of (19) with (14),then system (19) can be considered as the following system
| \begin{align} &\left[\begin{array}{*{20}c}\dot{\pmb Z}_{2}\\\dot{\pmb Z}_{3}\end{array}\right]=\left[\begin{array}{*{20}c} -k_{2}L&-k_{3}u_{1}^{d}L\\ u_{1}^{d}&0 \end{array}\right]\left[\begin{array}{*{20}c}{\pmb Z}_{2}\\{\pmb Z}_{3}\end{array}\right] \end{align} | (21) |
cascaded by
| \begin{align} \dot{\pmb Z}_{1}=-k_{0}\Lambda_{a_{i0}}({\pmb Z}_{1}-{\pmb Z}_{1}^{d})+L{\pmb Z}_{1}, \end{align} | (22) |
and the cascaded term is
| \begin{align} \left[\begin{array}{*{20}c}0&-k_{3}(\Lambda_{u_{i1}}-u_{1}^{d}I_{N})L\\ (\Lambda_{u_{i1}}-u_{1}^{d}I_{N})&0 \end{array}\right]\left[\begin{array}{*{20}c}{\pmb Z}_{2}\\{\pmb Z}_{3}\end{array}\right]. \end{align} | (23) |
1) Subsystem (22) will reach consensus exponentially on $u_{1}^{d}$ if the communication topology graph is connected and at least one of subsystems can access the reference signal system (2).
2) Subsystem (21) will also reach consensus when $u_{1}^{d}$ is persistent exciting signal according to Theorem 1.
3) It is easy to see that the cascaded term given in (23) satisfies the linear growth condition with respect to $[{\pmb Z}_{2},{\pmb Z}_{3}]^{\rm T}$.
Due to Lemma 3 of nonautonomous cascaded system,we can claim that consensus can be reached among the $N$ nonholonomic mobile robots under controllers (14) and (16) when communication topology is connected and at least one of them can access the reference signal.
Theorem 3. Practical consensus when $\pmb{u_{1}^{d}\rightarrow0}$ (or $\pmb{u_{1}^{d}=0}$).
The practical consensus problem of system (1) can be solved using controllers (15) and (16) when the communication topology is connected and at least one system can access the information of $x_{1}^{d}$.
Proof. 1) When $\rho_{i}\geq \varepsilon$
In this case,we inject some persistent exciting signals into the controller of $u_{i1}$ to guarantee controllability of the $i$th subsystem such as $k\sin(t)$ in (15). For each subsystem (22),it can be easily obtained that $u_{i1}$ will reach consensus on $k\sin(t)$ under connected communication topology. Then $\rho_{i}< \varepsilon$ can be obtained for subsystem (21) using the cascaded theory of nonautonomous system under controller (16) due to the exponential consensus result proposed in Theorem 1 when $\phi(t)=k\sin(t)$.
2) When $\rho_{i}< \varepsilon$
In this case,consensus of system (22) on the original reference signal will be obtained when the communication topology is connected,and at least one of the subsystems can access the reference signal,with each $\rho_{i}$ being allowed to travel freely in the $\varepsilon$ neighbourhood.
Then the practical consensus problem of multiple nonholonomic mobile robots can be solved using controllers given in (15) and (16) under connected communication topology and at least one system can access the reference signal.
Remark 4. Based on the results of Theorems 2 and 3, consensus of multiple nonholonomic mobile robots can be solved no matter $u_{1}^{d}$ is persistent exciting signal or not. To the authors' knowledge,this is the first result about consensus of nonholonomic system without restriction on $u_{1}^{d}$,unlike those in [27, 28, 29] where persistent excitation or nonzero constants have been imposed on cooperative control of this kind of systems.
Ⅴ. SIMULATION RESULTSIn this section,we illustrate our control methodology with the help of four nonholonomic mobile robots. Three different reference signals,which are $u_{i1}^{d}=0$,$u_{i1}^{d}=c\neq0$ and $u_{i1}^{d}=3\sin(0.2t)$,are considered in this section. As we have shown in previous sections,a lot of work has been done for persistent excitation reference but few works have considered the consensus problem of nonholonomic systems under reference target converging to zero. In our simulation,the communication topology is assumed to be connected and only one of the robots can access the information of reference signal.
A.When $\pmb{u_{i1}^{d}=0}$}Since $u_{i1}^{d}=0$ in this case,consensus of all state variables cannot be obtained using the previously obtained consensus protocols as shown in Section Ⅲ-B. According to Theorem 3,practical consensus can be realized using controllers (15) and (16),and the maximum error can be made as small as possible. In our simulation the maximum error is $\varepsilon=0.001$. Based on the consensus protocols proposed in Theorem 3,the simulation results are shown in Figs. 5$\sim$8.
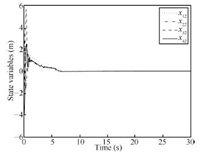
Figs. 5$\sim$7 have shown consensus of each state variable of four nonholonomic robots with respect to time. Consensus of their first state $x_{i1}$ and second state $x_{i2}$ is obtained as shown in Figs. 5 and 6,respectively. Only practical consensus of $x_{i3}$ is obtained as shown in Fig. 7 where $\varepsilon=0.001$. Fig. 8 shows the trajectories of each nonholonomic robot on the plane. Simulation results have shown effectiveness of the consensus protocols presented in Theorem 3.

|
Download:
|
| Fig. 5. Consensus of $x_{i1}$ ($i = 1,2, 3,4$). | |
|
Download:
|
| Fig. 6. Consensus of $x_{i2}$ ($i = 1,2,3,4$). | |

|
Download:
|
| Fig. 7. Consensus of $x_{i3}$ ($i = 1,2,3, 4$). | |
According to Definition 1,$u_{i1}^{d}=c\,(c \neq 0)$ in this case satisfies the persistent exciting condition. Based on the consensus protocols proposed in Theorem 2,the simulation results are shown in Figs. 9$\sim$12.

|
Download:
|
| Fig. 8. Trajectories of each nonholonomic robot. | |
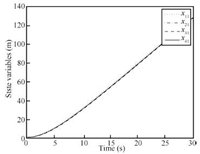
Due to the persistent excitation of $u_{i1}^{d}=c\,(c\neq 0)$,all of the first state variables $x_{i1}$ reach consensus on the ramp signal as shown in Fig. 9. Consensus of $x_{i2}$ and $x_{i3}$ is also realized using the consensus protocols given in Theorem 2 as shown in Figs. 10 and 11 with respect to time. Fig. 12 shows the trajectories of all nonholonomic robots on the plane. It is easy to see that all the state variables of nonholonomic mobile robots reach consensus and all of the robots move along a straight line in the end like one robot. Simulation results have show effectiveness of the consensus protocols presented in Theorem 2.
|
Download:
|
| Fig. 9. Consensus of $x_{i1}$ ($i = 1,2,3,4$). | |

|
Download:
|
| Fig. 10. Consensus of $x_{i2}$ ($i = 1,2,3, 4$). | |
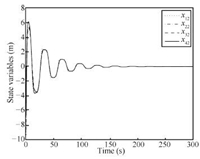
According to Definition 1,$u_{i1}^{d}=3\sin0.2t$ in this case also satisfies the persistent exciting condition. Based on the consensus protocols proposed in Theorem 2,the simulation results are shown in Figs. 13$\sim$16.
Due to the persistent excitation of $u_{i1}^{d}=3\sin0.2t$,the first state variables $x_{i1}$ of all robots reach consensus on the desired sinusoidal signal as shown in Fig. 13. Consensus of $x_{i2}$ and $x_{i3}$ using the consensus protocols given in Theorem 2 is shown in Figs. 14 and 15,respectively. Fig. 16 shows the trajectories of all nonholonomic robots on the plane. It is easy to see that all the state variables of nonholonomic mobile robots reach consensus and all of the nonholonomic robots move like a snake on the plane. Simulation results show effectiveness of the consensus protocols presented in Theorem 2.

|
Download:
|
| Fig. 11. Consensus of $x_{i3}$ ($i = 1,2,3,4$). | |

|
Download:
|
| Fig. 12. Trajectories of all nonholonomic robots. | |

|
Download:
|
| Fig. 13. Consensus of $x_{i1}$ ($i = 1,2,3, 4$). | |
|
Download:
|
| Fig. 14. Consensus of $x_{i2}$ ($i = 1,2,3,4$). | |

|
Download:
|
| Fig. 15. Consensus of $x_{i3}$ ($i = 1,2,3, 4$). | |

|
Download:
|
| Fig. 16. Trajectories of all nonholonomic robots. | |
Consensus problems of nonholonomic mobile robots both with and without persistent exciting signals have been considered in this paper. The cascaded theory of nonautonomous system is introduced to transform the consensus problem of nonholonomic mobile robots into consensus problems of two subsystems. Perturbation signals are injected into one of the subsystem to guarantee controllability of the nonholonomic mobile robots,when the group reference signal does not satisfy the condition of persistent excitation. Hybrid controllers are obtained in the end,and practical consensus is realized using the proposed controllers for this case. To the authors' knowledge,this work reports the first consensus result for multiple nonholonomic mobile robots when the group reference does not satisfy the condition of persistent excitation. The framework is extended to the consensus problem of nonholonomic chained form systems of $n$ dimensions in another paper. Fault detection and fault tolerant problem in the cooperative control of nonholonomic systems are also interesting problems for the authors to consider in future.
| [1] | DeGroot T, Morris H. Reaching a consensus. Journal of the American Statistical Association, 1974, 69(345):118-121 |
| [2] | Jadbabaie A, Lin J, Morse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Transactions on Automatic Control, 2003, 48(6):988-1001 |
| [3] | Ren W, Moore K, Chen Y Q. High-order and model reference consensus algorithms in cooperative control of multi vehicle systems. Journal of Dynamic Systems, Measurement, and Control, 2007, 129(5):678-688 |
| [4] | Olfati-Saber R, Fax J A, Murray R M. Consensus and cooperation in networked multiagent systems. Proceedings of the IEEE, 2007, 95(1):215-233 |
| [5] | Fax J A, Murray R M. Information flow and cooperative control of vehicle formations. IEEE Transactions on Automatic Control, 2004, 49(9):1465-1476 |
| [6] | Ren W. Multi-vehicle consensus with a time-varying reference state. Systems & Control Letters, 2007, 56(7-8):474-483 |
| [7] | Ren W, Atkins E. Distributed multi-vehicle coordinated control via local information exchange. International Journal of Robust and Nonlinear Control, 2007, 17(10-11):1002-1033 |
| [8] | Ren W. On consensus algorithms for double-integrator dynamics. IEEE Transactions on Automatic Control, 2008, 53(6):1503-1509 |
| [9] | Xie G M, Wang L. Consensus control for a class of networks of dynamic agents. International Journal of Robust and Nonlinear Control, 2007, 17(10-11):941-959 |
| [10] | Massioni P, Verhaegen M. Distributed control for identical dynamically coupled systems a decomposition approach. IEEE Transactions on Automatic Control, 2009, 54(1):124-135 |
| [11] | Popov A, Werner H. Robust stability of a multi-agent system under arbitrary and time-varying communication topologies and communication delays. IEEE Transactions on Automatic Control, 2012, 57(9):2343-2347 |
| [12] | Ghadami R. Distributed Control of Multi-agent Systems with Switching Topology, Delay, and Link Failure [Ph. D.dissertation], Northeastern University, United States, 2012 |
| [13] | Ghadami R, Shafai B. Decomposition-based distributed control for continuous-time multi-agent systems. IEEE Transactions on Automatic Control, 2013, 58(1):258-264 |
| [14] | Langbort C, Chandra R S, D'Andrea R. Distributed control design for systems interconnected over an arbitrary graph. IEEE Transactions on Automatic Control, 2004, 49(9):1502-1519 |
| [15] | Liu T F, Hill D J, Jiang Z P. Lyapunov formulation of ISS cyclic-smallgain in continuous-time dynamical networks. Automatica, 2011, 47(9):2088-2093 |
| [16] | Wang X, Liu T, Qin J. Second-order consensus with unknown dynamics via cyclic-small-gain method. IET Control Theory and Applications, 2012, 6(18):2748-2756 |
| [17] | Liao F, Lum K Y, Wang J L, Benosman M. Adaptive control allocation for non-linear systems with internal dynamics. IET Control Theory and Applications, 2009, 4(6):909-922 |
| [18] | Arcak M. Passivity as a design tool for group coordination. IEEE Transactions on Automatic Control, 2007, 52(8):1380-1390 |
| [19] | Ihle I A F, Arcak M, Fossen T I. Passivity-based designs for synchronized path-following. Automatica, 2007, 43(9):1508-1518 |
| [20] | Schlanbusch R, Loria A, Nicklasson P J. Cascade-based controlled attitude synchronization and tracking of spacecraft in leader-follower formation. International Journal of Aerospace Engineering, 2011, Article ID151262, DOI:10.1155/2011/151262 |
| [21] | Loría A. Cascades-based synchronization of hyperchaotic systems:application to chen systems. Chaos, Solitons & Fractals, 2011, 44(9):702-709 |
| [22] | Brockett R W. Asymptotic stability and feedback stabilization. Differential Geometric Control Theory. Boston:Birkhauser, 1983. 181-191 |
| [23] | Yamaguchi H, Arai T, Beni G. A distributed control scheme for multiple robotic vehicles to make group formations. Robotics and Autonomous Systems, 2001, 36(4):125-147 |
| [24] | Lin Z Y, Francis B, Maggiore M. Necessary and sufficient graphical conditions for formation control of unicycles. IEEE Transactions on Automatic Control, 2005, 50(1):121-127 |
| [25] | Ghabcheloo R. Coordinated Path Following of Multiple Autonomous Vehicles[Ph. D. dissertation], Technical University of Lisbon, Portugal, 2007 |
| [26] | Ceccarelli N, Di Marco M, Garulli A, Giannitrapani A. Collective circular motion of multi-vehicle systems. Automatica, 2008, 44(12):3025-3035 |
| [27] | Liu T F, Jiang Z P. Distributed formation control of nonholonomic mobile robots without global position measurements. Automatica, 2013, 49(2):592-600 |
| [28] | Dong W J, Farrell J A. Cooperative control of multiple nonholonomic mobile agents. IEEE Transactions On Automatic Control, 2008, 53(6):1434-1448 |
| [29] | Lee D J. Passive decomposition and control of nonholonomic mechanical systems. IEEE Transactions on Robotics, 2010, 26(6):978-992 |
| [30] | Zhai G S, Takeda J, Imae J, Kobayashi T. Towards consensus in networked non-holonomic systems. IET Control Theory and Applications, 2010, 4(10):2212-2218 |
| [31] | Lefeber E. Tracking Control of Nonlinear Mechanical Systems.[Ph. D. dissertation], Universiteit Twente, The Netherlands, 2000 |
| [32] | Slotine J J, Li W P. Applied Nonlinear Control. Englewood Cliffs, NJ:Prentice-Hall, 1991. 115 |
| [33] | Panteley E, Loria A. On global uniform asymptotic stability of nonlinear time-varying systems in cascade. Systems & Control Letters, 1998, 33(2):131-138 |
| [34] | Isidori A. Nonlinear Control Systems. London:Springer, 1995. 427 |
| [35] | Murray R M. Recent research in cooperative control of multivehicle systems. Journal of Dynamic Systems, Measurement, and Control, 2007, 129(5):571-583 |
| [36] | Cao K C, Jiang B, Chen Y Q. Cooperative control design for nonholonomic chained-form systems. International Journal of Systems Science, DOI:10.1080/00207721.2013.809615 |
 2014, Vol.1
2014, Vol.1 


