I. INTRODUCTION

Research on multi-agent systems (or networked cooperative systems) with applications to the cooperation of unmanned aerial vehicles (UAVs),autonomous underwater vehicles (AUVs),robots,scheduling of automated highway systems has attracted much attention in the past two decades^{[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]}. Efforts towards stabilization and tracking control of multi-fully actuated ocean surface vessels as the need for rescuing,exploring and preserving the oceanic environments have gained significant momentum.

In most of the present work,every agent is required to follow a specified path or track a predefined position in the formation^{[9, 10, 11, 12]}. Nonlinear robust adaptive control strategy was developed to force an underactuated surface ship to follow a predefined path at a desired speed in ^[13]. Moreover,feedback control law was designed to stabilize the underactuated vessel to a desired constant position and orientation in ^[14]. In ^[15],a combination of line-of-sight path following and nonlinear synchronization strategies was studied. Nontrivial coordinate changes,graph theory,and stability theory of linear time-varying systems were used to design cooperative control laws for underactuated vessels to perform a geometric pattern^[2].

It is interesting to observe from examples of group behavior in the nature that accurate specification of the path of each agent in the group seems to be not necessary. Swarming behavior is more common where agents are loosely distributed within a moving target region,not requiring specific orders or positions of the agents inside the region. The region reaching control concept was presented for robot manipulator,in which the desired objective can be specified as a region instead of a point in ^[16],and ^[17] proposed the new region-reaching controller for an underwater vehicle mounted with a manipulator. It has been shown that region reaching tasks save energy and result in faster motion. In ^[18],an adaptive region boundary-based concept was presented for an AUV,in which the controller was designed to allow the convergence of the vehicle to the boundary or a motionless region surface regardless of its initial position. Region following formation control concept has been proposed^{[19, 20]},where all the robots stay within a moving region as a group,while maintaining a minimum distance among themselves. Recently,the region following control concept has been developed for general multi-agent systems with high-order dynamics in previous work^[21].

In this paper,we propose a decentralized cooperative controller for multi-fully actuated ocean vessel systems. A group of ocean vessels with limited sensing ranges are driven into a moving target region without collisions,and the connectivity preservation of the dynamic interaction network is guaranteed. By using the objective function,the desired region can be specified as an arbitrary shape,and hence we can form different formations. The decentralized controller permits the ocean vessels in the group to only communicate with their neighbors. It reduces communication or sensing requirement,and is relatively more scalable with respect to the group size. We introduce the artificial potential functions to preserve the connectivity of the network and guarantee no collisions between any ocean vessels^{[22, 23]}. The chosen potential functions possess the special property of approaching infinity whenever its arguments approach some limits^{[24, 25]}.

The handling of unknown perturbations to the nominal model,in the form of parametric and functional uncertainties,unmodeled dynamics,and disturbances from the environment,is an important issue of model-based control of ocean vessels. Traditional model-based adaptive controllers may not be applicable since they are useful only when dealing with systems in which the dynamics are linear-in-the-parameters,the uncertainties are parametric and time-invariant,and the regressors are exactly known^[26]. For overcoming the limitations of model-based adaptive controllers,we adopt approximation-based control techniques to compensate for functional uncertainties and unknown disturbances from the environment.

The main contributions of this work are listed as follows:

1) The detailed theoretical formation,which can enable a swarm of multi-fully actuated ocean surface vessels to track a moving target region,is proposed in the presence of uncertainties and unknown disturbances.

2) The artificial potential function is subtly introduced to preserve the connectivity of the network. Connectivity is a common assumption in the consensus analysis of multi-agent systems. In fact,it is not always valid in the networked systems whose sensors are distance dependent,and thus in order to accomplish a cooperative task,the connectivity of the network is required to be maintained.

3) The collision avoidance potential function is chosen to prevent the collisions between vessels when they are inside their danger ranges. Especially,the length of vessel is considered in the designing such that the collision avoidance function approaches infinity whenever any other vessels come in contact with the vessel,i.e.,a collision occurs.

4) The approximation-based controller for fully actuated surface vessels is designed using Lyapunov synthesis. Such approximators can use a standard regressor function whose structure is independent of the ocean vessel's dynamic characteristics,thus it increases the portability of the same control algorithm on different ocean vessel systems.

The remainder of the paper is organized as follows. In Section II,the problem is stated and some preliminaries are presented. In Section III,the region tracking controller of multi-fully actuated surface vessel systems is designed and the effectiveness of our algorithm is analysed. In Section IV,simulation results are presented to illustrate the performance of the proposed region tracking controller. Finally,we conclude the paper in Section V.

II. PROBLEM FORMULATION

A.Vessel Dynamics Consider a group of $N$ fully actuated vessels,and the multiple-input-multiple-output (MIMO) dynamics of the 3 degrees-of-freedom (3DOF) vessel $i$ is

\begin{align} &\dot\eta_i=R_i(\eta_i)\nu_i,{\rm n} num\end{align}

(1)

\begin{align} &M_i\dot\nu_i=\tau_i-C_i(\nu_i)\nu_i-D_i(\nu_i)\nu_i+R_i(\eta_i)^{\rm T}d_i, \end{align}

(2)

where $\eta_i=[x_i,y_i,\psi_i]^{\rm T} \in {\bf R}^3$,$ i=1,2,\cdots,N$,is the vector representing the inertial earth-fixed frame position and heading,respectively; $\nu_i=[u_i,v_i,r_i]^{\rm T}\in {\bf R}^3 $ is the vector representing the vessel surge,sway, and yaw velocities,respectively as shown in Fig. 1; $d_i=[d_{i1},d_{i2},d_{i3}]^{\rm T}\in {\bf R}^3$ is the vector representing the unknown disturbance from the environment,and/or unmodeled dynamics,among others; and $\tau_i\in {\bf R}^3$ is the vector of input signals. The matrices $R_i(\eta_i)$,$M_i$, $C_i(\nu_i)$,and $D_i(\nu_i)$ are given as below: \begin{align*} &R_i(\eta_i)=\left [ \begin{array}{ccc} \cos {\psi_i}&-\sin {\psi_i}&0\\ \sin {\psi_i}&\cos {\psi_i}&0\\ 0&0&1\\ \end{array}\right],\nonumber\\[2mm] &M_i=\left [ \begin{array}{ccc} m_{i11}&0&0\\ 0&m_{i22}& m_{i23}\\ 0&m_{i32}&m_{i33}\\ \end{array}\right], \end{align*} \begin{align*} &C_i(\nu_i)=\left [ \begin{array}{ccc} 0&0&c_{i13}\\ 0&0&c_{i23}\\ -c_{i13}&-c_{i23}&0\\ \end{array}\right],\nonumber\\[2mm] &D_i(\nu_i)=\left [ \begin{array}{ccc} d_{i11}&0&0\\ 0&d_{i22}& d_{i23}\\ 0&d_{i32}&d_{i33}\\ \end{array}\right], \end{align*} with \begin{align*} &m_{i11}=m_i-X_{i\dot u},\quad\quad m_{i22}=m_i-Y_{i\dot v},{\rm n} num\\ &m_{i23}=m_ix_{ig}-Y_{i\dot r},\quad m_{i32}=m_ix_{ig}-N_{i\dot v},{\rm n}num\\ &m_{i33}=I_{iz}-N_{i\dot r},{\rm n}num\\ &c_{i13}=-m_{i22}v_i-m_{i23}r_i,\quad c_{i23}=m_{i11}u_i,{\rm n}num\\ &d_{i11}=-X_{iu}-X_{iu|u|}|u_i|-X_{iuuu}u_i^2,{\rm n}num\\ &d_{i22}=-Y_{iv}-Y_{i|v|v}|v_i|-Y_{i|r|v}|r_i|,{\rm n}num\\ &d_{i23}=-Y_{ir}-Y_{i|v|r}|v_i|-Y_{i|r|r}|r_i|,{\rm n}num\\ &d_{i32}=-N_{iv}-N_{i|v|v}|v_i|-N_{i|r|v}|r_i|,{\rm n}num\\ &d_{i33}=-N_{ir}-N_{i|v|r}|v_i|-N_{i|r|r}|r_i|{\rm n}num. \end{align*} where $m_i$ is the mass of the vessel $i$,$I_{iz}$ is the inertia of vessel about the $Z_i$-axis of the body-fixed frame,$x_{ig}$ is the $X_i$-coordinate of the vessel center of gravity,and the other symbols are hydrodynamic derivatives. Using semi-empirical methods or hydrodynamic computation programs,the coefficients in $M_i$ and $C_i(\nu_i)$ are determined quite accurately^[26]. There exists difficulty in finding the coefficients in $D_i(\nu_i)$,and thus,we rewrite (1) as

\begin{align} &\dot\eta_i=R_i(\eta_i)\nu_i,\label{remodel}{\rm n}num \end{align}

(3)

\begin{align} &M_i\dot \nu_i=\tau_i-C_i(\nu_i)\nu_i+\kappa_i(\nu_i)+g_i(\eta_i,\nu_i), \end{align}

(4)

where the smooth function vector $\kappa_i(\nu_i)$ is the known part of $-D_i(\nu_i)\nu_i$,and $g_i(\eta_i,\nu_i)$,$i=1,\cdots,n$ are unknown smooth functions,so that $\kappa_i(\nu_i) +g_i(\eta_i,\nu_i) =R_i(\eta_i)^{\rm T}d_i-D_i(\nu_i)\nu_i$. The system inertial matrix $M_i = M_i^{\rm T}>0$,and premultiplying by $M_i^{-1}$,model (2) is in parametric strict feedback form. To design the tracking controller for multi-fully actuated ocean surface vessel systems,we impose the following assumptions on the communication and initial conditions between the vessels in the group.

${\bf Assumption 1.}$ All vessels have the same characteristics.

We associate the vessels with nodes in a graph and information exchange with its edges. The communication graph $\mathcal{G}$ is defined for describing the inter-vessel communication. We use ${G}_i$ to denote the set of indices for those vessels having communication with vessel $i$.

${\bf Assumption 2.}$ The communication graph $\mathcal{G}$ is an undirected graph and connected initially.

${\bf Definition 1.}$ The undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ consists of a set of vertices $\mathcal{V}=\{1,\cdots,N\}$ indexed by the group members,and a set of edges,$\mathcal{E}=\{(i,j)\in \mathcal{V}\times\mathcal{V}\big|i\in {G}_j\}$ containing pairs of nodes that show inter-vessel communication specifications.

${\bf Assumption 3.}$ Each vessel has a communication range $R$. For simplicity,we assume that all vessels move in a two-dimensional (2-D) workspace. Their position in the workspace is denoted by $q_i=[x_i,y_i]^{\rm T}$,and $\eta_i=[q_i^{\rm T},\psi_i]^{\rm T}$. The set ${G}_i$ can be defined as the set that vessel $i$ can communicate when it is located at its initial position:

\begin{align} {G}_i=\left\{j\in\mathcal{V},j\neq i~\big|\| q_i(0)-q_j(0)\| \leq R\right\}. \end{align}

(5)

The objective is to design an adaptive neural network region tracking controller for each vessel such that all vessels can converge to a common moving target region without collisions between vessels in the group,while the connectivity of the communication graph remains for all time. The target region function,$R_T(\cdot)$,can be specified by an inequality function as follows: $R_T(\cdot)=[R_{T_1}(\cdot),\cdots,R_{T_i}( \cdot),\cdots,R_{T_N}( \cdot)]^{\rm T}\leq0,$ where $R_{T}(\cdot)\in \bf{R}$ is a continuous scalar function with continuous first partial derivative,so that the desired target region for vessel $i$,$i=1,\cdots,N$,can be simply specified as a circle with radius $r_0$,as $R_{T_i}( \tilde q_{i,0}(t))=\parallel q_i(t)-q_0(t)\parallel^2-r_0^2\leq0,$ where $q_0(t)=[q_{0,x}(t),q_{0,y}(t)]^{\rm T}$ is the center of the moving target region,and $\tilde q_{i,0}(t)=q_i(t)-q_0(t)$. 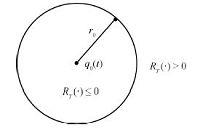An illustration of the target region function is shown in Fig. 2. Clearly,if $r_0$ reduces to zero,the desired target region reduces to a point,that is,the moving target region tracking control concept is a generalization of path following.

${\bf Assumption 4.}$ The position $q_0(t)$ and velocity $\dot q_0(t)$ of the center of the moving target region are continuous and bounded.

${\bf Assumption 5.}$ The target region is big enough to accommodate all vessels and their own communication ranges.

In the later part of this paper,the time argument will be omitted if no confusion is expected. We mathematically formulate the control objective by defining the variable $\psi_{i,d}$ as $\arctan ({\dot q_{0,y}\over \dot q_{0,x}})$. Then,the function for the control objective is presented as

\begin{align} F_i(\tilde \eta_{id})=&\ (x_i-q_{0,x})^2+(y_i-q_{0,y})^2 -r_0^2+(\psi_{i}-\psi_{i,d})^2={\rm n}num\end{align}

(6)

\begin{align} &\ \|\tilde \eta_{id}\|^2-r_0^{2}, \end{align}

(7)

where $\tilde \eta_{id}=\eta_i-\eta_{i,d}$,and $\eta_{i,d}=[q_{0,x},q_{0,y},\psi_{i,d}]$.

B.Potential Functions

The potential functions consist of target tracking function, collision avoidance function,and connectivity maintenance function,which are specified as below.

1) Target tracking function: The target tracking function is designed for each vessel to track the common target region by putting a penalty on the tracking errors. The target tracking function ${P_{i,0}}:{{\bf{R}}^3} \to {\bf{R}}$ for vessel $i$ is chosen as follows:

\begin{align} P_{i,0}(\tilde\eta_{id} )&=&\begin{cases} 0,&R_{T_i}( \tilde q_{i,0})\leq0,\\[2mm] {\dfrac{c_i}{ 2}}F_i^2( \tilde\eta_{id}),& R_{T_i}( \tilde q_{i,0})>0, \end{cases} \end{align}

(8)

where $c_i$ is a positive constant. The target tracking function has the following properties:

1) $P_{i,0}=0$,if $R_{T_i}(\tilde q_{i,0})\leq0$;

2) $P_{i,0}>0$,if $R_{T_i}(\tilde q_{i,0})>0$;

3) $P_{i,0}\to\infty $,if $R_{T_i}(\tilde q_{i,0})\to\infty.$

2) Collision avoidance function:${\bf Definition 2.}$ Each vessel has a danger range,which is centered at the vessel,with radius $r$ $(r＜R)$.

To prevent the collisions between vessels when they are inside their danger ranges,the collision avoidance function is chosen. ${H}_i$ is presented to denote the set containing all those vessels within the danger range of vessel $i$ as follows ${H}_i =\left\{ j\in \mathcal{V},j\neq i\ \big|\| \tilde q_{i,j}\|^2-r^2\leq 0\right\},$ where $\tilde q_{i,j}=q_{i}-q_{j}$. The collision avoidance function $P_{i,j}$ for vessel $i$ is chosen as follows:

\begin{align} \label{collpot} P_{i,j}(\tilde q_{i,j})=\begin{cases} 0,& \| \tilde q_{i,j}\|>r,\\ c_{i,j}\ln \left(\dfrac{r^2-L^2}{\| \tilde q_{i,j}\|^2-L^2}\right)^2,& \| \tilde q_{i,j}\| \leq r, \end{cases} \end{align}

(9)

where $c_{i,j} = c_{j,i}$ is a positive constant. The length of vessel,$L$ $(L＜r)$,is considered in the designing such that it is equal to infinity whenever any vessels come in contact with the vessel $i$,i.e.,a collision occurs. The collision avoidance function $P_{i,j}$ has the following properties:

1) $P_{i,j}=0$,if $\|\tilde q_{i,j} \|>r$;

2) $P_{i,j}>0$,if $\|\tilde q_{i,j} \|\leq r$;

3) $P_{i,j}$ is monotonically increasing with the decreasing of $\|\tilde q_{i,j} \|$,if $\|\tilde q_{i,j} \|\leq r$;

4) $P_{i,j}\to\infty$,if $\|\tilde q_{i,j} \|\to L$. 3) Connectivity maintenance function: Connectivity is a common assumption in the consensus analysis of multi-agent systems. In fact,it is not always valid in the networked systems whose sensors are distance dependent. Therefore the connectivity maintenance potential function is designed to preserve the connectivity of the network,that is,the vessels are initially located in the communication zone of a vessel,and they will remain in this area for all time. We define the connectivity maintenance function as follows:

\begin{align} Q_{i,j}( \tilde q_{i,j})=c'_{i,j}\ln \left( \dfrac{R^2}{R^2-\| {\tilde q}_{i,j}\|^2}\right)^2, \end{align}

(10)

where $c'_{i,j} = c'_{j,i}$ is positive,and $\| \tilde q_{i,j}\|$ $\in$ $[0,{ R})$. The connectivity maintenance function has the following properties:

1) $Q_{i,j}\to\infty$,if $\|\tilde q_{i,j} \|\to { R}$;

2) $Q_{i,j}$ is continuous and differentiable,$\forall \|\tilde q_{i,j} \|$ $\in$ $[0,{ R})$.

C. Function Approximation

In control engineering,linearly parameterized neural network has been successfully used to approximate the following unknown continuous function $F_i(Z_i):{\bf R}^q \to \bf{R}$ for $i$-th vessel^{[27, 28]}: $F_i(Z_i)=\phi_i^{\rm T}(Z_i)\varphi_i+\varepsilon_i(Z_i),$ where $Z_i=[z_{i1},z_{i2},\cdots,z_{iq}]^{\rm T}\in {\bf R}^q$ is the input vector,$\varphi_i$ $\in$ ${\bf R}^{l}$ is the weight vector with the neural network node number $l$,$\phi_i(Z_i)\in {\bf R}^{l}$ is a vector of known continuous basis functions,and $\varepsilon_i(Z_i)$ is called the neural network approximation error which satisfies $|\varepsilon_i(Z_i)|\leq \varepsilon_i^{*}$,$\forall Z_i\in \Omega_{Z_i}$ with the unknown constant $\varepsilon_i^{*}>0$.

According to the universal approximation property,if $l$ is chosen sufficiently large,$\phi_i^{\rm T}(Z_i)\varphi_i$ can smoothly approximate any continuous function $F_i(Z_i)$ over a compact set $\Omega_{Z_i}$ $\subset$ ${\bf R}^q$ to an arbitrary degree of accuracy as $F_i(Z_i)=\phi_i^{\rm T}(Z_i)\varphi_i^*+\varepsilon_i(Z_i),\quad \forall Z_i\in \Omega_{Z_i}\subset {\bf R}^q,$ where $\varphi_i^*$ is the ideal constant weight vector,and $\varepsilon_i(Z_i)$ is the approximation error for the special case where $\varphi_i=\varphi_i^*$. The ideal weight vector $\varphi_i^*$ is an artificial quantity required for analytical purposes. $\varphi_i^*$ is defined as the value of $\varphi_i$ that minimizes $|\varepsilon_i|$ for all $Z_i\in \Omega_{Z_i}\subset {\bf R}^q$,that is $ \varphi_i^*=\arg\min_{\varphi_i\in{\bf R}^l}\Big\{ \sup _{Z_i\in\Omega_{Z_i}}|F_i(Z_i)-\phi_i^{\rm T}(Z_i)\varphi_i|\Big\}. $

${\bf Lemma 1}$^[29]. The following inequality holds for any $\epsilon$ $>$ $0$ and for any $\eta\in \bf{R}$ $ 0\leq|\eta|-\eta\tanh\bigg( {\eta\over \epsilon}\bigg)\leq \kappa\epsilon,{\rm n}num $ where $\kappa$ is a constant that satisfies $\kappa=\exp[-(\kappa+1)]$,i.e.,$\kappa$ $=$ $0.2785$. The scalar $\epsilon>0$ is a (small) positive design constant,and $\tanh(\cdot)$ denotes the hyperbolic tangent function.

III. CONTROL DESIGN AND STABILITY ANALYSIS

In this section,we present the decentralized adaptive neural network control scheme for vessel $i$ to achieve the control objective. Feedforward approximators are used to compensate for unknown nonlinear functions. Using the potential functions in the first step of recursion,we can guarantee that all vessels can track the moving target region without collisions,and the connectivity of the network remains for all time. The second step follows the standard backstepping procedure with the quadratic Lyapunov functions^[30]. According to the analysis above,the whole potential function can be written as $ V_{1}=\sum_{i=1}^{N}P_{i,0} +\sum_{i=1}^{N}\sum_{j\in { H} _{i}}P_{i,j} +\sum_{i=1}^{N}\sum_{j\in { G}_{i}}Q_{i,j}. $ Then, the derivative of $V_1$ can be expressed as

\begin{align} \dot{V}_{1}=&\ \sum_{i=1}^{N}\big(\frac{\partial P_{i,0}}{\partial\tilde{\eta}_{id}}\dot{\tilde{\eta}}_{id}+ \sum_{j\in { H}_{i}}\frac{\partial P_{i,j}}{\partial{\tilde q}_{i,j}}\dot{\tilde{q}}_{i,j}+ \sum_{j\in { G}_{i}}\frac{\partial Q_{i,j}}{\partial{\tilde q}_{i,j}}\dot{\tilde{q}}_{i,j}\big)={\rm n}num \end{align}

(11)

\begin{align} &\ \sum_{i=1}^{N}\frac{\partial P_{i,0}}{\partial\tilde{\eta}_{id}}(\dot{\eta}_{i} -\dot{\eta}_{i,d})+\sum_{i=1}^{N} \sum_{j\in { H}_{i}}\frac{\partial P_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j}) +{\rm n}num \end{align}

(12)

\begin{align} &\ \sum_{i=1}^{N}\sum_{j\in { G}_{i}}\frac{\partial Q_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j}). \end{align}

(13)

According to the fact that the interactions between vessels are bi-directional,we can obtain

\begin{align} &\sum_{i=1}^{N}\sum_{j\in { H}_{i}}\dfrac{\partial P_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j})={\rm n}num \end{align}

(14)

\begin{align} &\qquad \sum_{i=1}^{N}\sum_{j\in { H}_{i}}\dfrac{\partial P_{i,j}}{\partial{\tilde q}_{i,j}}[(\dot{q}_{i}-\dot{q}_{0})-(\dot{q}_{j}-\dot{q}_{0})]={\rm n}num\end{align}

(15)

\begin{align} &\qquad \sum_{i=1}^{N}\sum_{j\in { H}_{i}}\left[\dfrac{\partial P_{i,j}}{\partial{ q}_{i}}(\dot{q}_{i}-\dot{q}_{0})-\dfrac{\partial P_{i,j}}{\partial{ q}_{i}} (\dot{q}_{j}-\dot{q}_{0})\right]={\rm n}num\end{align}

(16)

\begin{align} &\qquad 2\sum_{i=1}^{N}\sum_{j\in { H}_{i}}\dfrac{\partial P_{i,j}}{\partial{ q}_{i}}(\dot{q}_{i}-\dot{q}_{0}). \end{align}

(17)

Similarly,we can obtain $\sum_{i=1}^{N}\sum_{j\in {G}_{i}}\frac{\partial Q_{i,j}}{\partial{\tilde q}_{i,j}}(\dot{q}_{i}-\dot{q}_{j})=2\sum_{i=1}^{N}\sum_{j\in {G}_{i}}\frac{\partial Q_{i,j}}{\partial{ q}_{i}}(\dot{q}_{i}-\dot{q}_{0}).$ Then,we have

\begin{align} \dot{V}_{1} =&\ \sum_{i=1}^{N}\frac{\partial P_{i,0}}{\partial\tilde{\eta}_{id}}(\dot{\eta}_{i} - \dot{\eta}_{i,d})+2\sum_{i=1}^{N}\sum_{j\in {H}_{i}} \frac{\partial P_{i,j}}{\partial{q}_{i}}(\dot{q}_{i}-\dot{q}_{0}) +{\rm n}num\end{align}

(18)

\begin{align} &\ 2\sum_{i=1}^{N}\sum_{j\in {G}_{i}}\frac{\partial Q_{i,j}}{\partial{q}_{i}}(\dot{q}_{i}-\dot{q}_{0}). \end{align}

(19)

According to the theory of matrix calculus,we obtain $ \sum_{i=1}^N\sum_{j\in {H}_i}{{\rm p} P_{i,j}\over {\rm p} q_{i}}(\dot q_i-\dot q_0)=\sum_{i=1}^N\sum_{j\in {H}_i} {{\rm p} P_{i,j}\over{\rm p} \eta_{i}}(\dot \eta_i-\dot \eta_{i,d}),{\rm n}num\\ $ and $\sum_{i=1}^{N}\sum_{j\in {G}_{i}}{{\rm p} Q_{i,j}\over{\rm p} q_{i}}(\dot q_i-\dot q_0)=\sum_{i=1}^N\sum_{j\in {G}_i}{{\rm p} Q_{i,j}\over{\rm p} \eta_{i}}(\dot \eta_i-\dot \eta_{i,d}). $ Then,the derivative of $V_1$ is given by

\begin{eqnarray} \dot{V}_{1} = \sum_{i=1}^{N}\nabla_{\eta_{i}} V_{1}\cdot(\dot{\eta}_{i} -\dot{\eta}_{i,d}),\label{eq:nabla1} \end{eqnarray}

(20)

where $ \nabla_{\eta_{i}}V_{1}=\frac{\partial P_{i,0}}{\partial\eta_{i}}+2\sum_{j\in {H}_{i}}\frac{\partial P_{i,j}}{\partial\eta_{i}}+2\sum_{j\in {G}_{i}}\frac{\partial Q_{i,j}}{\partial\eta_i}.$

${\bf Step 1.}$ Denote the error coordinates

\begin{align} &z_{i,1} = \eta_{i}-\eta_{i,d}\label{z1},\end{align}

(21)

\begin{align} &z_{i,2} = \nu_{i}-\alpha_{i},\end{align}

(22)

\begin{align} &\tilde{\varphi}_{i} = \varphi_{i}^{*}-\hat{\varphi}_{i}, \end{align}

(23)

where $\alpha_{i}$ is a stabilizing function vector to be designed,$\hat{\varphi}_{i}$ is the parameter estimate,and $\tilde{\varphi}_{i}$ is the estimated error vector of the parameter. Differentiating $z_{i,1}$ with respect to time yields

\begin{eqnarray} \dot{z}_{i,1} = R_{i}(\eta_{i})\nu_{i}-\dot{\eta}_{i,d}.\label{dotz1} \end{eqnarray}

(24)

We choose the potential function as the Lyapunov function candidate. Then,we have

\begin{eqnarray} \dot{V}_{1} = \sum_{i=1}^{N}\nabla_{\eta_{i}}V_{1}\cdot[R_{i}(\eta_{i}) \nu_{i}- \dot{\eta}_{i,d}]. \end{eqnarray}

(25)

Noting the property $R_i(\eta_{i})R_i^{\rm T}(\eta_{i})=I$,if $\nu_{i}= R_i^{\rm T}(\eta_{i})$ $\times$ $( -k_{i,1}\nabla_{\eta_{i}}^{\rm T} V_{1}+\dot{\eta}_{i,d})$,we have the following $\dot{V}_{1} =-\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2},$ which means that the artificial potential function $V_{1}$ keeps decreasing as long as $\|\nabla_{\eta_{i}}V_{1}\|\ne0$,and $V_{1}$ can converge to a neighborhood of the origin while $\nu_{i}$ approaches $ R_i^{\rm T}(\eta_{i}) (-k_{i,1}\nabla^{\rm T}_{\eta_{i}}V_{1} +\dot{\eta}_{i,d})$. Hence,the virtual control $\alpha_{i}$ can be chosen as $ \alpha_{i}=R_{i}^{\rm T}(\eta_{i}) (-k_{i,1}\nabla^{\rm T}_{\eta_{i}}V_{1} +\dot{\eta}_{i,d}). $ Then according to the Young$'$s inequality,the time derivative of $V_{1}$ along the trajectories of (26) is given by

\begin{align} \dot{V}_{1}=& -\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2} +\sum_{i=1}^{N} \nabla_{\eta_{i}}V_{1}\cdot R_{i}(\eta_{i})z_{i,2}\leq{\rm n}num\end{align}

(26)

\begin{align} & -\sum_{i=1}^{N}k_{i,1}^{'}\| \nabla_{\eta_{i}}V_{1}\|^{2} +\varepsilon,\end{align}

(27)

where $k_{i,1}$,$k_{i,1}^{'}$,and $\varepsilon=\sum_{i=1}^{N}{\parallel R_i\parallel^2\parallel z_{i,2}\parallel^2\over 2}$ are positive.

${\bf Step 2.}$ In this step,we design the control law recursively to stabilize the error dynamics of $z_{i,2}$. Differentiating $z_{i,2}$ with respect to time yields

\begin{equation} \dot{z}_{i,2} =M_{i}^{-1} \big[\tau_{i}-C_{i}(\nu_{i})\nu_{i}+\kappa_{i}(\nu_{i}) +\phi_{i}^{\rm T}\varphi_{i}^{*}+\varepsilon_{i}\big] -\dot{\alpha}_{i}. \end{equation}

(28)

Consider the Lyapunov function candidate

\begin{equation} V_{2}=V_{1}+\sum_{i=1}^{N}\frac{1}{2} z_{i,2}^{\rm T} z_{i,2}+ \sum_{i=1}^{N} \frac{1}{2} \tilde{\varphi}_{i}^{\rm T}\Gamma_{i}^{-1}\tilde{\varphi}_{i}, \end{equation}

(29)

where $\Gamma_{i}=\Gamma_{i}^{\rm T}>0$,the time derivative of $V_{2}$ is

\begin{align}\label{dv2} \dot{V}_{2} = & -\sum_{i=1}^{N} k_{i,1}\|\nabla_{\eta_{i}}V_{1} \|^{2} +\sum_{i=1}^{N}\nabla_{\eta_{i}}V_{1} \cdot R_{i}(\eta_{i})z_{i,2} +{\rm n}num\end{align}

(30)

\begin{align} & \ \sum_{i=1}^{N}z_{i,2}^{\rm T}\{M_{i}^{-1} \big[\tau_{i}-C_{i}(\nu_{i})\nu_{i} + \kappa_{i}(\nu_{i}) +{\rm n}num \end{align}

(31)

\begin{align} & \ \phi_{i}^{\rm T}\varphi_{i}^{*}+ \varepsilon_{i}\big]-\dot{\alpha}_{i}\} -\sum_{i=1}^{N}\tilde{\varphi}_{i}^{\rm T} \Gamma_{i}^{-1}\dot{\hat{\varphi}}_{i}. \end{align}

(32)

The desired control law and the adaptive update law for $\hat{\varphi}_{i}$ are then designed as

\begin{align} \tau_{i} = & -M_{i}R_{i}^{\rm T}(\eta_{i})\nabla_{\eta_{i}}^{\rm T} V_{1}- k_{i,2}M_{i}z_{i,2} +C_{i}(\nu_{i})\nu_{i} -{\rm n}num\label{control} \end{align}

(33)

\begin{align} & \ \kappa_{i}(\nu_{i})-\phi_{i}^{\rm T}\hat{\varphi}_{i}+M_{i}\dot{\alpha}_{i} -\varepsilon_{i}^{*}\tanh \big(\frac{z_{i,2}^{\rm T} M_{i}^{-1}\varepsilon_{i}^{*}}{\epsilon_{i}}\big), \end{align}

(34)

\begin{align} \dot{\hat{\varphi}}_{i} = &\ \Gamma_{i}(\phi_{i}M_{i}^{-1}z_{i,2}- \sigma_i \hat{\varphi}_i). \label{update} \end{align}

(35)

Substituting (34) and (35) into equation (33),we can obtain

\begin{align} \dot{V}_{2} = & -\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2} -\sum_{i=1}^{N}k_{i,2}\|z_{i,2}\|^{2} + \label{stabilization}{\rm n}num \end{align}

(36)

\begin{align} &\ \sum_{i=1}^{N}\bigg[z_{i,2}^{\rm T}M_{i}^{-1}\varepsilon_{i} -z_{i,2}^{\rm T} M_{i}^{-1}\varepsilon_{i}^{*} \tanh\big(\frac{z_{i,2}^{\rm T}M_{i}^{-1} \varepsilon_{i}^{*}} {\epsilon_{i}}\big)\bigg] +{\rm n}num \end{align}

(37)

\begin{align} &\ \sum_{i=1}^N\tilde\phi_i^{\rm T}\sigma_i(\varphi_i^{*}- \tilde\varphi_i), \end{align}

(38)

where $\epsilon_{i},\sigma_i$ and $k_{i,2}$ are positive constants. It is clear that $ z_{i,2}^{\rm T}M_{i}^{-1}{\varepsilon_{i}}\leq \parallel z_{i,2}^{\rm T}M_{i}^{-1}\varepsilon_{i}^{*} \parallel. $ According to Lemma 1, we can obtain

\begin{align}&&z_{i,2}^{\rm T}M_{i}^{-1}\varepsilon_{i} -z_{i,2}^{\rm T}M_{i}^{-1}\varepsilon_{i}^{*} \tanh\big(\frac{z_{i,2}^{\rm T}M_{i}^{-1} \varepsilon_{i}^{*}} {\epsilon_{i}}\big)\leq\kappa\epsilon_i,{\rm n}num \end{align}

(39)

and by Young$'$s inequality,we have $ \sum_{i=1}^N\tilde\phi_i^{\rm T}\sigma_i(\varphi_i^{*}- \tilde\varphi_i)\leq -\sum_{i=1}^N{\sigma_i\parallel \tilde \varphi_i\parallel^2\over 2}+ \sum_{i=1}^N{\sigma_i\parallel \varphi_i^{*}\parallel ^2\over 2}. $ Therefore,the derivative of $V_2$ satisfies the following inequality

\begin{align} \dot{V}_{2} \leq & -\sum_{i=1}^{N}k_{i,1}\|\nabla_{\eta_{i}}V_{1}\|^{2} - \sum_{i=1}^{N}k_{i,2}\|z_{i,2}\|{}^{2} - {\rm n}num \end{align}

(40)

\begin{align} &\ \sum_{i=1}^N{\sigma_i\parallel \tilde \varphi_i\parallel^2\over 2}+c_0, \end{align}

(41)

where $c_0=\sum_{i=1}^{N}\big(\kappa\epsilon_{i}+ {\sigma_i\parallel \varphi_i^{*}\parallel^2\over 2}\big)$ is positive. As the potential function $V_1$ and $\parallel\nabla_{\eta_i}V_1 \parallel$ change simultaneously with the same arguments,we can know $V_{2}$ can converge to a bounded compact set as the time approaches infinity. Therefore the boundary of the potential function,$V_1$,can be guaranteed.

${\bf Theorem 1.}$ Consider the vessel dynamics (1) under Assumptions 1 $\sim$ 5,with region tracking control law (34) and the update law (35). For initial conditions starting in any compact set $\Omega_0$,the whole potential function $V_1$ can converge to a bounded compact set,which gives rise to the convergence of $\eta_i$,$i=1,2,\cdots,N$,to the desired target set,with the connectivity of the network maintained,while no collisions happen between any vessels for all $t>0$.

${\bf Proof.}$ First,we prove the convergence of vessel $i$ to the common moving target region.

Since the whole artificial potential function $V_1$ is bounded,the potential functions $P_{i,0}$,$P_{i,j}$,and $Q_{i,j}$ are all bounded. Therefore,the tracking error of each ocean vessel can converge to an adjustable neighborhood of the origin,although some of them do not access the desired target region directly.

Next,we show that there are no collisions between any vessels, and the connectivity of the network can be maintained for all time.

Since the function $P_{i,j}$ is bounded,hence,according to the property of $P_{i,j} $,$\parallel \tilde q_{i,j}\parallel> L$, i.e.,there are no collisions between any vessels for all $t>0$. Similarly,according to the property of $Q_{i,j} $,we can obtain $\parallel\tilde q_{i,j}\parallel ＜ R$,that is,the connectivity of the network can be maintained for all $t$ $>$ $0$.

IV. SIMULATION RESULTS

In our simulation study,we consider the model vessel called CyberShip II,a 1 : 70 scale supply vessel replica built in a marine control laboratory in the Norwegian University of Science and Technology. The model can be rewritten as (2),with parameters obtained from ^[26]. Fig. 3 shows the communication relationships among vessels.

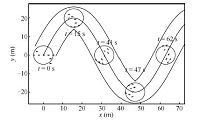
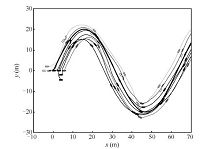
We consider a group of vessels with $N=8$,the danger range radius $r=2.0$ m and the communication range radius $R=3.0$ m. The vessels are initialized randomly around the target region with $q_0(0)=[0.0$,$0.0]^{\rm T}$,$\eta_1(0)=[-5.0$,$0.0$,$0.0]^{\rm T}$,$\eta_2(0)=[-3.5$,$2.0$,$0.0]^{\rm T}$,$\eta_3(0)=[-2.5$, 0.0,$0.0]^{\rm T}$,$\eta_4(0)=[0.0$,0.0,$0.0]^{\rm T}$, $\eta_5(0)= [2.5$,0.0,$0.0]^{\rm T}$,$\eta_6(0)=[5.0$,0.0, $0.0]^{\rm T}$,$\eta_7(0)=[3.5$,$-2.0$,$0.0]^{\rm T}$, $\eta_8(0)=[3.5$,$-4.5$,$0.0]^{\rm T}$. The center of the common target region,$q_0$,moves along the desired trajectory $q_0(t)=[t$,$20\sin(0.1t)]^{\rm T}$ with $r_0$ $=$ $5.0$ m. Simulation results are shown in Figs. 4 $\sim$ 6.

Fig. 4 clearly shows the tracking process of all vessels which can successfully track the common moving target region,and the boundness of $P_{i,0}$ in Fig. 6 further confirms it. The trajectories of all vessels and the center of the moving target region are shown in Fig. 5. We can see all vessels can synchronously track the center of the moving target region. From Figs. 4 and 5,we can also find the connectivity of the network remains for all time. Moreover,the boundness of the connectivity maintenance function,$Q_{i,j}$,in Fig. 6 further confirms the connectivity maintenance. Fig. 6 also shows the boundness of collision avoidance function $P_{i,j}$. Therefore,we obtain that no collisions among vessels can be guaranteed.

V. CONCLUSION

In this paper,due to the advantages of the target region tracking control for achieving better performance and energy saving,stable approximation-based region tracking control has been designed for a group of surface vessels in the presence of time-varying environmental disturbances,unmodeled dynamics,or parametric/functional uncertainties. Simulation results have demonstrated that all vessels can successfully track the common moving target region without collisions. At the same time,the connectivity of the network can be maintained for all time.

Acknowledgements

The authors would like to thank Dr. Ren Bei-Bei,who is affiliated with Department of Mechanical Engineering,Texas Tech University, USA,for her valuable inputs to the paper.