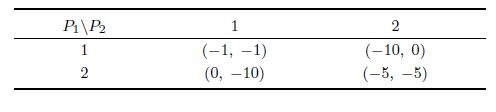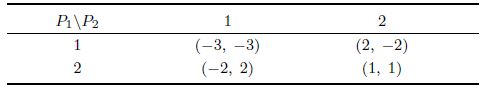2. Institute of Sstronautics, Harbin Institute of Technology, Harbin 150080, China;
3. Institute of Systems Science, Chinese Academy of Sciences, Beijing 100190, China
The evolutionary game was firstly proposed by biologists about four decades ago. It was used in biology to model the evolution of species in nature. Later on,it had various applications not only to biology but also to economics,social sciences,etc.[1, 2]. In an evolutionary game there are usually many players,and the players as nodes form a complete graph. That is,each player plays with all others,and repeats the game for many or even infinite times.
Though it has been proved very useful,this approach has an obvious drawback,that is,the topology describing the relationship of players is ignored. Recently,the network[3, 4, 5, 6] was borrowed to describe the topology of players in an evolutionary game. Roughly speaking,an evolutionary game with a graph using players as nodes is a networked evolutionary game (NEG). For the last decade or so, the networked evolutionary game has become a hot topic[7, 8, 9]. Some survey papers provided a general description and overall picture for the characteristics and research topics of NEGs[10, 11].
The progress of the study of NEGs is rapid and many interesting results have been reported. For instance,the evolution of cooperation on scale-free networks was investigated in [12, 13], evolution on two interdependent networks was considered in [14, 15],etc. We refer to [16] for some recent developments.
To the best of our knowledge,most of researches on NEGs are based on Monte Carlo and similar simulations. It can hardly be used for general,e.g.,asymmetric networks. Using semi-tensor product of matrices,this paper proposes a new framework to model the networked game. Then we present an algorithm to calculate the mixed strategy Nash equilibrium of a multi-player game. By exploring the relationship between local and global Nash equilibriums,the method is applied to static network games. Finally,a sufficient condition is provided to construct the Nash equilibrium of networked evolutionary game via the Nash equilibrium of its corresponding one step static game.
The paper is organized as follows. Section II introduces some notations and gives a brief survey on semi-tensor product of matrices. Section III analyzes the structure of networked evolutionary games. Then a rigorous mathematical model for NEGs is presented in Section IV. Section V proposes a method to calculate the Nash equilibrium for multi-player games. In Section VI,we first investigate the static Nash equilibrium of networked game. Then the relationship between local and global Nash equilibriums is revealed, and it is used to calculate the static Nash equilibrium of networked games. Finally,a sufficient condition is obtained to construct Nash equilibrium of NEG via its corresponding one step static Nash equilibriums. Section VII contains some concluding remarks.
II. PRELIMINARIES A.Notations1) ${M_{m \times n}}$ is the set of $m\times n$ real matrices.
2) $Col_i(M)$ is the $i$th column of matrix $M$; $Col(M)$ is the set of columns of $M$.
3) ${\cal D}_k=\{1,2,\cdots,k\}$.
4) $\delta _n^i=Col_i(I_n)$,i.e.,it is the $i$th column of the identity matrix.
5) $D_n=Col(I_n)$.
6) $M\in {\cal M}_{m\times n}$ is called a logical matrix if $Col(M)\subset D_m$,the set of $m\times n$ logical matrices is denoted by ${\cal L}_{m\times n}$.
7) Assume $L\in {\cal L}_{m\times n}$,and $$ L=\left[\delta_m^{i_1}\quad\delta_m^{i_2}\quad\cdots\quad\delta_m^{i_n}\right], $$ then its shorthand form is $$ L=\delta_m\left[i_1\quad i_2\quad\cdots\quad i_n\right]. $$
8) $r=(r_1,\cdots,r_k)^{\rm T}\in R^k$ is called a probabilistic vector,if $r_i\geq 0$,$i=1,\cdots,k$,and $ \sum_{i=1}^kr_i=1. $
The set of $k$ dimensional probabilistic vectors is denoted by $\varUpsilon_k$.
9) Let $R\in {\cal M}_{m\times n}$. If $Col(R)\subset \varUpsilon_m$,then $R$ is called a probabilistic matrix. The set of $m\times n$ dimensional probabilistic matrices is denoted by $\varUpsilon_{m\times n}$.
B.Semi-tensor Product of MatricesSemi-tensor product of matrices is the main tool in this paper. The following is a brief survey.
${\bf Definition 1.}$ Let $A\in {\cal M}_{m\times n}$ and $B\in
{\cal M}_{p\times q}$. Denote by $ t=lcm(n,p)$ the least common
multiple of $n$ and $p$. Then we define the semi-tensor product
(STP) of $A$ and $B$ as
\begin{align}\label{1.1}
A\ltimes B=\left(A\otimes I_{t/n}\right)\left(B\otimes
I_{t/p}\right)\in {\cal M}_{(mt/n) \times (qt/p)}.
\end{align}
(1)
${\bf Remark 1.}$ 1) When $n=p$,$A\ltimes B=AB$. Therefore the STP is a generalization of the conventional matrix product. So symbol "$ \ltimes$" can be omitted,and the matrix product is assumed to be STP in the sequel.
2) STP keeps all the major properties of the conventional matrix product valid,including the associative law and distributive law.
We cite some basic properties which are used in this note.
${\bf Proposition 1.}$ 1) For any two matrices,
\begin{align}\label{1.2}
(A\ltimes B)^{\rm T}=B^{\rm T}\ltimes A^{\rm T}.
\end{align}
(2)
\begin{align}\label{1.3}
(A\ltimes B)^{-1}=B^{-1}\ltimes A^{-1}.
\end{align}
(3)
${\bf Proposition 2.}$ Let $X\in {\bf R}^t$ be a column vector. Then
for matrix $M$,
\begin{align}\label{1.4}
X\ltimes M=\left(I_t\otimes M\right) \ltimes X.
\end{align}
(4)
${\bf Definition 2.}$ Define a matrix
\begin{align}\label{1.5}
W_{[n,m]}= \delta_{mn}&\left[ 1,m+1,2m+1,\cdots,(n-1)m+1,\right.\nonumber\\
&\ \ 2,m+2,2m+2,\cdots,(n-1)m+2,\nonumber\\
&\ \ \cdots,\nonumber\\
&\ \left. n,m+n,2m+n,\cdots,mn \right]\in {\cal M}_{mn\times
mn},
\end{align}
(5)
${\bf Proposition 3.}$ Let $X \in R^m$ and $Y\in R^n$ be two column
vectors. Then
\begin{align}\label{1.6}
W_{[m,n]}\ltimes X\ltimes Y=Y\ltimes X.
\end{align}
(6)
Finally,we consider how to express a Boolean function into the algebraic form.
${\bf Theorem 1.}$ Let $f:{\cal B}^n \to {\cal B}$ be a Boolean
function expressed as
\begin{align}\label{1.7}
y=f(x_1,\cdots,x_n),
\end{align}
(7)
\begin{align}\label{1.8}
1\sim \delta_2^1,\quad 0\sim \delta_2^2.
\end{align}
(8)
\begin{align}\label{1.9}
y=M_f\ltimes_{i=1}^nx_i,
\end{align}
(9)
Assume $x_i\in {\cal D}_{k_i}$,$i=1,\cdots,n$. We identify ${\cal D}_k\sim D_k$ by
\begin{align}\label{1.10}
1\sim \delta_k^1,\; 2\sim \delta_k^2,\; \cdots,\; k\sim \delta_k^k.
\end{align}
(10)
Theorem 1 can be generalized as
${\bf Theorem 2.}$ Let $f(x_1,\cdots,x_n):\prod_{i=1}^n{\cal
D}_{k_i} \to {\cal D}_{k_0}$. Using identification (10),
$f$ can be expressed in the vector form as
\begin{align}\label{1.11}
y=M_f\ltimes_{i=1}^nx_i,
\end{align}
(11)
Assume there are $n$ players (or agents) denoted by $N=$ $\{1$,2, $\cdots,n\}$,and $E\subset N\times N$ describes the relation between players. Then a network graph $(N,E)$ is obtained.
${\bf Definition 3.}$ 1) $j$ is said to be in the neighborhood of $i$,denoted by $j\in U_i$,if either $(i,j)\in E$ or $(j,i)\in E$. Hence the definition of neighborhood hereafter is independent of the directions of edges,even if the graph is directed.
2) As a convention,we define $i\in U_i$.
3) If $k\in U_j$ and $j\in U_i$,then $k$ is said to be in the sub-neighborhood of $i$,denoted by $k\in \bar{U}_i$.
${\bf Definition 4.}$ Game $G$ is called a fundamental network game (FNG),if
1) $G$ has two players;
2) Both players have the same set of strategies,denoted by $S=\{1,2,\cdots,k\}$. $G$ is symmetric if $$ c_{1,2}(s_i,s_j)=c_{2,1}(s_j,s_i),\quad \forall s_i,s_j\in S. $$
Now each player $i$ plays the FNG $G$ pairwisely with each of its
neighbors $j$,$j\in U_i\backslash\{i\}$. The overall payoff of
$i$ is the average of its payoffs $c_{i,j}$,precisely,
\[{c_i} = \frac{1}{{|{U_i}| - 1}}\sum\limits_{j \in {U_i}\backslash \{ i\} } {{c_{i,j}}} ,\quad i = 1,2, \cdots ,n.\]
(12)
${\bf Definition 5.}$ A strategy updating rule (SUR),denoted by
$\Pi$,is a rule for each player $i$ to update its strategy
$x_i(t+1)$,based on its neighbors$'$ information at time $t$.
Precisely,it can be expressed as
\begin{align}\label{2.2}
x_i(t+1)=f_i\left(\left\{x_j(t),c_j(t)\big|j\in
U_i\right\}\right),\quad i=1,2,\cdots,n.
\end{align}
(13)
Note that the $f_i$ in (13) will be uniquely determined by the SUR. Throughout this paper we use only the following two typical SURs:
1) $\Pi_1$ (Unconditional imitation[8]):
The strategy of player $i$ at time $t+1$,$x_i(t+1)$,is selected
as the best strategy among the strategies of its neighbors $j$ $\in$
$U(i)$ at time $t$. Precisely,if
\begin{align}\label{2.3}
j^*=\arg\max\limits_{j\in U(i)}c_j(x(t)),
\end{align}
(14)
\begin{align}\label{2.4}
x_i(t+1)=x_{j^*}(t).
\end{align}
(15)
\begin{align}\label{2.5}
j^*=\min\{\mu | \mu \in \arg\max\limits_{ j\in U(i)}c_j(x(t))\}.
\end{align}
(16)
This method leads to a deterministic $k$-valued dynamics.
2) $\Pi_2$ (Simplified Fermi rule[17, 18]):
Player $i$ chooses randomly a neighborhood $j\in U(i)$ and
compares $c_j(x(t))$ with $c_i(x(t))$ to determine $x_i(t+1)$ as
\begin{align}\label{2.6}
x_i(t+1)=\begin{cases}
x_j(t),&\quad c_j(x(t))> c_i(x(t)),\\[2mm]
x_i(t),&\quad \mbox{otherwise}.
\end{cases}
\end{align}
(17)
Now we are ready to give a rigorous definition of NEGs[19].
${\bf Definition 6.}$ An NEG,denoted by a triple $((N,E)$,$G$, $\Pi)$,consists of three factors: 1) the network graph $(N,E)$; 2) an FNG $G$; 3) an SUR $\Pi$.
Note that a network graph could be directed,which is applicable to the case when the FNG is asymmetric. In this case $(i,j)\in E$ means in the FEG $i$ is the first player $1$ and $j$ is the second player $2$.
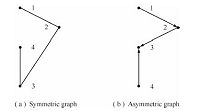
${\bf Example 1.}$ 1) Consider a networked game described by an undirected graph in Fig. 1 (a). Assume the strategy set $S_0$ $=$ $\{1,2\}$,and the payoff bi-matrix of the $1$st FNG $G_1$,played by player pairs $(1,2)$ and $(2,3)$,is shown in Table I,and the payoff bi-matrix of the $2$nd FNG $G_2$,played by $(3,4)$,is shown in Table II.
|
Download:
|
| Fig. 1.Two kinds of graphs. | |
|
|
Table I PAYOFF BI-MATRIX FOR Fig. 1 (a): $(1,2)$,$(2,3)$ |
|
|
Table II PAYOFF BI-MATRIX FOR Fig. 1 (a): $(3,4)$ |
Since $G_1,G_2$ are symmetric,this is a symmetric NEG.
2) Consider a networked game described by directed graph in Fig. 1 (b). Assume $S_0=\{1,2\}$,and the payoff bi-matrix of the unique FNG $G_3$,played by $(4,2)$,$(2,1)$,$(1,3)$,$(3,2)$,is shown in Table III.
|
|
Table III ASYMMETRIC PAYOFF BI-MATRIX FOR Fig. 1 (b) |
Since $G_3$ is asymmetric,this is an asymmetric NEG.
This example will be further investigated in the sequel.
IV. NETWORK PROFILE DYNAMICS
From the SUR equation (2.2),since $c_j(t)$ depends on $x_k(t)$,
$k\in U_j$,one sees easily that (2.2) can be rewritten as
\begin{align}\label{3.1}
x_i(t+1)=f_i\left(\left\{x_k(t)\big|k\in
\bar{U}_i\right\}\right),\quad i=1,2,\cdots,n.
\end{align}
(18)
This is a standard $k$-valued logical dynamic network (might be a probabilistic one). If we can figure out $f_i$ in (3.1),the network profile dynamics can be constructed via standard procedures[20]. In fact,it can be determined by SUR. It will be illustrated via an example later.
According to Theorem 2,(3.1) can be expressed into the vector
form as
\begin{align}\label{3.101}
x_i(t+1)=M_ix(t),\quad i=1,2,\cdots,n,
\end{align}
(19)
Then the network profile dynamics is obtained as
\begin{align}\label{3.102}
x(t+1)=Mx(t).
\end{align}
(20)
1) Case 1 (deterministic model): when $M_i\in {\cal L}_{k\times
k^n}$,$i=$ 1,$\cdots$,$n$,and
\begin{align}\label{3.103}
M=M_1*M_2*\cdots *M_n.
\end{align}
(21)
2) Case 2 (probabilistic model):
\begin{align}\label{3.104}
M_i=M_i^j,~~\mbox{with}~ P=p_i^j,\ \ j=1,\cdots,r_i,\ i=1,\cdots,
n,
\end{align}
(22)
\begin{align}\label{3.105}
\begin{aligned}
M&=M_1^{j_1}* M_2^{j_2}*\cdots* M_n^{j_n},~~\mbox{with}~ P=\prod_{i=1}^np_i^{j_i},\\
~&\qquad\qquad~~~~~~~~~ j_i=1,\cdots,r_i;~~ i=1,\cdots,n.
\end{aligned}
\end{align}
(23)
${\bf Example 2.}$ Recall Example 1.
1) Consider part 1) in Example 1 and assume the SUR is $\Pi_1$:
$x_1(t+1)$ depends on its sub-neighborhood $\bar{U}_1=\{1,2,3\}$ only. For instance,if $x_1=1$,$x_2=2$,$x_3=2$,then using Table I, we have \begin{align*} &c_1=c_{12}=-10,\ \ c_{21}=0,\ \ c_{23}=-5, \\ & c_2=c_{21}+c_{23}=-5. \end{align*} Then $$ f_1(1,2,2)=x_2=2. $$ Similarly,all the values of $f_1$ are calculated and listed in Table IV.
|
|
Table IV CALCULATING $f_i$ ($Pa$: PAYOFF,$Pr$: PROFILE) |
That is,in the vector form:
\begin{align*}
x_1(t+1)=&\ f_1(x_1(t),x_2(t),x_3(t))=\\
&\ \delta_2[1,1,2,2,2,2,2,2]x_1(t)x_2(t)x_3(t).
\end{align*}
Similarly,we can obtain
\begin{align*}
x_2(t+1)=&\ f_2(x_1(t),x_2(t),x_3(t),x_4(t))=\\
&\
\delta_2[1,1,1,2,2,2,2,2,2,1,2,2,2,2,2,2]\ltimes\\
&\ x_1(t)x_2(t)x_3(t)x_4(t),\\[2mm]
x_3(t+1)=&\ f_3(x_1(t),x_2(t),x_3(t),x_4(t))=\\
&\ \delta_2[1,1,1,2,2,2,1,2,1,1,1,2,1,2,1,2]\ltimes\\
&\ x_1(t)x_2(t)x_3(t)x_4(t),
\end{align*}
and
\begin{align*}
x_4(t+1)=&\ f_4(x_2(t),x_3(t),x_4(t))=\\
&\ \delta_2[1,1,1,2,1,2,1,2]x_2(t)x_3(t)x_4(t).
\end{align*}
Define $x(t)=\ltimes_{i=1}^4x_i(t)$. Then we can express the above
$4$ equations as
\begin{align}\label{3.2}
x_i(t+1)=M_ix(t),\quad i=1,2,3,4,
\end{align}
(24)
\begin{align}\label{3.3}
x(t+1)=Mx(t),
\end{align}
(25)
2) Consider part 2) in Example 1 and assume the SUR is $\Pi_2$:
Now only players $2$ and $3$ have different choices. We use $f_2^1$ to describe the SUR when player $2$ chooses to compete with player $1$,and $f_2^2$ the SUR when player $2$ chooses player $3$; we use $f_3^1$ for the case player $3$ chooses player $2$ and $f_3^2$ the case player $3$ chooses player $4$. Using Table III,the $f_i$, $i$ $=$ $1,2,3,4$ can be calculated,which are shown in Table V.
It comes from Table V that $$ f_i(t+1)=M_i\ltimes_{j=1}^4x_i(t)=M_ix(t), $$
|
|
Table V CALCULATING $f_i$ ($Pa$: PAYOFF,$Pr$: PROFILE) |
1) $ M_1=\delta_2[1,1,1,1,1,1,2,2,1,1,1,1,2,2,2,2]; $
2) $ M_2=\begin{cases} M_2^1,&p_2^1=0.5,\\ M_2^2,& p_2^2=0.5, \end{cases} $ where \begin{align*} M_2^1=&\ \delta_2[1,1,1,1,1,1,2,2,1,1,1,1,2,2,2,2],\\ M_2^2=&\ \delta_2[1,1,2,2,1,1,2,2,1,1,2,1,1,1,2,2]; \end{align*}
3) $ M_3=\begin{cases} M_3^1,& p_3^1=0.5,\\ M_3^2,& p_3^2=0.5, \end{cases} $ where \begin{align*} M_3^1=&\ \delta_2[1,1,2,2,1,1,2,2,1,1,2,1,1,1,2,2],\\ M_3^2=&\ \delta_2[1,1,2,2,1,1,1,2,1,2,2,2,1,1,1,2]; \end{align*}
4) $ M_4=\delta_2[1,1,2,2,1,1,1,2,1,2,2,2,1,1,1,2]. $
We conclude that the overall network profile dynamics is
\begin{align}\label{3.4}
x(t+1)=Mx(t),
\end{align}
(26)
First,we consider a static networked game (NG). From (12)
it is clear that the payoffs are $k$-valued pseudo-logical
functions. Then,they can be expressed into the algebraic form as
\begin{align}\label{4.1}
c_i=G_i\ltimes_{j=1}^nx_j,\quad i=1,\cdots,n,
\end{align}
(27)
In this subsection,we mainly consider games with mixed strategies. Because the existence of Nash equilibrium is assured as the mixed strategy is allowed[22, 23].
The following lemma comes from definitions immediately.
${\bf Lemma 1.}$ Consider the payoffs in algebraic form as
(27). If player $i$ takes mixed strategies
$$
x_i=\left[x_i^1,\;\cdots,\;x_i^{k}\right]^{\rm T}\in
\varUpsilon_{k},\quad i=1,\cdots,n,
$$
then the expected values are
\begin{align}\label{4.2}
E_i=G_i\ltimes_{j=1}^nx_j,\quad i=1,\cdots,n.
\end{align}
(28)
In Example 1,the composition of strategy dynamics of all players into profile dynamics has been discussed. In the following,we consider the case of mixed strategy.
${\bf Lemma 2.}$ Given $y_i\in \varUpsilon_k$,$i=1,\cdots,m$,
$$
y=\ltimes_{i=1}^my_i,
$$
\begin{align}\label{4.3}
D^{[m,k]}_i=diag\{\underbrace{{\bf 1}_{k^{m-1}},\cdots,{\bf
1}_{k^{m-1}}}_k\}W_{[k^{i-1},k]}.
\end{align}
(29)
\begin{align}\label{4.4}
y_i=D^{[m,k]}_iy,\quad i=1,\cdots,m.
\end{align}
(30)
Then it is clear that%
$$
\Psi y=\Psi
\begin{bmatrix}y_1^1\\y_1^2\\\vdots\\y_1^k\end{bmatrix}y^{(-1)} =
\begin{bmatrix}y_1^1 {\bf 1}_{k^{m-1}}y^{(-1)} \\y_1^2 {\bf
1}_{k^{m-1}}y^{(-1)} \\\vdots\\y_1^k {\bf
1}_{k^{m-1}}y^{(-1)}\end{bmatrix}=y_1.
$$
It follows that
$$
D^{[m,k]}_iy=\Psi y_iy^{(-i)}=y_i.
$$
${\bf Remark 2.}$ Assume $y_i$,$x_j\in D_k$,$i=1,\cdots,m$,
$j=1$,$\cdots$,$n$. Let
\begin{align}\label{4.5}
y_i=M_ix,\quad i=1,\cdots,m,
\end{align}
(31)
\begin{align}\label{4.6}
y=Mx,
\end{align}
(32)
For the probabilistic case,where $y_i,x_j\in \varUpsilon_k$,the structure matrix can be calculated by $(23)$.
To calculate the Nash equilibrium(s),we need the following lemma.
It can be verified by a straightforward computation.
${\bf Lemma 3.}$ Assume $X\in \varUpsilon_p$ and $Y\in
\varUpsilon_q$. We define two dummy matrices,named
"front-maintaining operator (FMO)" and "rear-maintaining operator (RMO)" respectively as
$$
D_f^{p,q}=\delta_p\left[\underbrace{1\cdots 1}_q\;\underbrace{2\cdots
2}_q\;\cdots\;\underbrace{p\cdots p}_q\right],
$$
$$
D_r^{p,q}=\delta_q\left[\underbrace{\underbrace{12\cdots
q}~\underbrace{12\cdots q}~\cdots~\underbrace{12\cdots
q}}_p\right].
$$
Then we have
\begin{align}\label{4.7}
&D_f^{p,q}XY=X,\end{align}
(33)
\[{D_r^{p,q}XY = Y.}\]
(34)
Next,we express $x_i$ by its independent components as \[{x_i} = {\left[ {x_i^1, \cdots ,x_i^{{k_i} - 1},1 - \sum\limits_{j = 1}^{k - 1} {x_i^j} } \right]^{\text{T}}},\quad i = 1, \cdots ,n.\]
Then we have
\begin{align}\label{4.9}
\begin{aligned}
\frac{\partial E_i}{\partial x_i^j}&=G_ix_1\cdots x_{i-1}\left(\delta_{k}^j-\delta_{k}^{k}\right)x_{i+1}\cdots x_n=\\
~~~&~~G_iW_{[k,k^{i-1}]} \left(\delta_{k}^j-\delta_{k}^{k}\right) x_1\cdots x_{i-1}x_{i+1}\cdots x_n=\\
~~~&~~G_iW_{[k,k^{i-1}]} \left(\delta_{k}^j-\delta_{k}^{k}\right) x_1\cdots x_{i-1}D_r^{k,k^{n-i}]}x_ix_{i+1}\cdots x_n=\\
~~~~~&~~G_iW_{[k,k^{i-1}]} \left(\delta_{k}^j-\delta_{k}^{k}\right) \left(I_{k^{i-1}}\otimes D_r^{[k,k^{n-i}]}\right)\ltimes_{j=1}^n x_j=\\
~~~~~&~~G_i\gamma_i^jx,~~~~~~~~~j=1,\cdots,k-1,\;\; i=1,\cdots,n,
\end{aligned}
\end{align}}
(35)
\begin{align}\label{4.900}
\gamma_i^j=W_{[k,k^{i-1}]} \left(\delta_{k}^j-\delta_{k}^{k}\right)
\left(I_{k^{i-1}}\otimes D_r^{[k,k^{n-i}]}\right).
\end{align}
(36)
Using $\gamma_i^j$,we construct a matrix as
\begin{align}\label{4.901}
\Gamma=\begin{bmatrix}
G_1\gamma_1^1\\
\vdots\\
G_1\gamma_1^{k-1}\\
G_2\gamma_2^1\\
\vdots\\
G_2\gamma_2^{k-1}\\
\vdots\\
G_n\gamma_n^1\\
\vdots\\
G_n\gamma_n^{k-1}\\
\end{bmatrix}.
\end{align}
(37)
${\bf Theorem 4.}$ $x_i\in \varUpsilon_{p_i}$,$i=1,\cdots,n$ is a
mixed strategy Nash equilibrium,if and only if they satisfy
\[\Gamma x = \Gamma \ltimes _{i = 1}^n{x_i} = 0.\]
(38)
${\bf Proof.}$ Necessity is obvious. As for the sufficiency,since $\frac{\partial c_i}{\partial x_i^j}$ is independent of $x_i^s$, $s=1,\cdots,p_i-1$,then $$ E_i(x_1^*\cdots x_i^*\cdots x_n^*)=c_i(x_1^*\cdots x_i\cdots x_n^*),\quad \forall x_i\in \varUpsilon_{k}. $$ The conclusion follows.
B.Numerical AlgorithmIn this section,we explore a numerical algorithm for calculating Nash equilibrium. We define some sets: \begin{align*} &S=\left\{x\in R^{k^n} ~\big|~ \Gamma x=0\right\}, \\ &H=\varUpsilon_{k^n}\cap S, \\ &U=\left\{\ltimes_{i=1}^nx_i~\big|~x_i\in \varUpsilon_{k},\; i=1,\cdots,n\right\}. \end{align*}
The following proposition comes from the definition.
${\bf Proposition 4.}$ $x\in \varUpsilon_p$ is a Nash equilibrium, if and only if $$ x\in H\cap U. $$
According to this proposition,we define two mappings:
1) $\varphi:U \to H$ as
\[\varphi (x) = \arg \mathop {\min }\limits_y y - x,\quad y \in H,\;x \in U.\]
(39)
2) $\pi:H \to U$ as
$$\pi (y) = _{i = 1}^n\left[ {D_i^{[n,k]}y} \right].$$
(40)
To see $\varphi$ is well defined,we consider the following
problem: for a given $x_0\in R^n$,minimize $(y-x_0)^{\rm
T}(y-x_0)$,i.e.,
\[\min {y^{\text{T}}}y - 2x_0^{\text{T}}y,\]
(41)
\[{\text{s}}.{\text{t}}.\left\{ {\begin{array}{*{20}{l}}
{Ay = b,} \\
{y \geqslant 0,}
\end{array}} \right.\]
(42)
This is a quadratic programming problem; by checking the Karush-Kuhn-Tucker (KKT) condition,the solution is unique. That is, $\varphi$ is well defined[24].
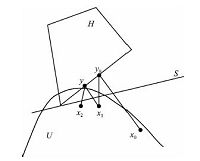
Now we are ready to present the following algorithm,as shown in Fig. 2.
|
Download:
|
| Fig. 2.Searching algorithm. | |
${\bf Algorithm 1.}$
${\bf Step 1.}$ Choose a point $x_0\in U$. Find $y_0=\varphi(x_0)\in H$,and then find $x_1=\pi(y_0)\in U$.
${\bf Step $k$.}$ Find $y_{k-1}=\varphi(x_{k-1})\in H$,and then find $x_k$ $=$ $\pi(y_{k-1})$ $\in$ $U$.
${\bf Last step.}$ If
\[\pi ({y_k}) = {y_k}\]
(43)
${\bf Example 4.}$ Consider the game of rock-scissors-paper (R-S-P). The payoff bi-matrix is shown in Table VI.
|
|
Table VI PAYOFF BI-MATRIX OF |
Now assume there is a network of three players and the network graph is a complete graph,i.e., any two nodes are connected. It is easy to figure out the payoff matrix as shown in Table VII.
|
|
Table VII OVERALL PAYOFF BI-MATRIX |
It follows that \begin{align*} G_1=&\ [ 0,1,-1,1,2,0,-1,0,-2,-2,-1,0,-1,0,\\ ~&~~ 1,0,1,2,2,0,1,0,-2,-1,1,-1,0 ],\\ G_2=&\ [ 0,1,-1,-2,-1,0,2,0,1,1,2,0,-1,0,\\ ~&~~ 1,0,-2,-1,-1,0,-2,0,1,2,1,-1,0 ],\\ G_3=&\ [ 0,-2,2,1,-1,0,-1,0,1,1,-1,0,2,0,\\ ~&~ {-2},0,1,-1,-1,0,1,0,1,-1,-2,2,0 ]. \end{align*}
Using formula (36),we set \[\begin{gathered} {R_1} = {G_1}\gamma _1^1 = {G_1}(\delta _3^1 - \delta _3^3)D_r^{[3,{3^2}]}, \hfill \\ {R_2} = {G_1}\gamma _1^2 = {G_1}(\delta _3^2 - \delta _3^3)D_r^{[3,{3^2}]}, \hfill \\ {R_3} = {G_2}\gamma _2^1 = {G_2}{W_{[3,3]}}(\delta _3^1 - \delta _3^3)\left( {{I_3} \otimes D{r^{[3,3]}}} \right), \hfill \\ {R_4} = {G_2}\gamma _2^2 = {G_2}{W_{[3,3]}}(\delta _3^2 - \delta _3^3)\left( {{I_3} \otimes D_r^{[3,3]}} \right), \hfill \\ {R_5} = {G_3}\gamma _3^1 = {G_3}{W_{[3,9]}}(\delta _3^1 - \delta _3^3)\left( {{I_9} \otimes D_r^{[3,1]}} \right), \hfill \\ {R_6} = {G_3}\gamma _3^2 = {G_3}{W_{[3,9]}}(\delta _3^2 - \delta _3^3)\left( {{I_9} \otimes D_r^{[3,1]}} \right). \hfill \\ \end{gathered} \] Then it is easy to calculate $R_i$,$i=1,2,3,4,5,6$,as \begin{align*} R_1=&\ [ -2, 1, -2, 1, 4, 1, -2, 1, -2, -2, 1, -2, 1, 4,\\ &~~ 1, -2, 1, -2, -2, 1, -2, 1, 4, 1, -2, 1, -2 ],\\ R_2=&\ [ -4, -1, -1, -1, 2, 2, -1, 2, 2, -4, -1, -1, -1, 2,\\ ~&~~ 2, -1, 2, 2, -4, -1, -1, -1, 2, 2, -1, 2, 2 ], \end{align*} \begin{align*} R_3=&\ [ -2, 1, -2, -2, 1, -2, -2, 1, -2, 1, 4, 1, 1, 4,\\ ~&~~ 1, 1, 4, 1, -2, 1, -2, -2, 1, -2, -2, 1, -2 ],\\ R_4=&\ [ -4, -1, -1, -4, -1, -1, -4, -1, -1, -1, 2, 2, -1, 2,\\ ~&~~ 2, -1, 2, 2, -1, 2, 2, -1, 2, 2, -1, 2, 2 ],\\ R_5=&\ [ -2, -2, -2, 1, 1, 1, -2, -2, -2, 1, 1, 1, 4, 4,\\ ~&~~ 4, 1, 1, 1, -2, -2, -2, 1, 1, 1, -2, -2, -2 ],\\ R_6=&\ [ -4, -4, -4, -1, -1, -1, -1, -1, -1, -1, -1, -1, 2, 2,\\ ~&~~ 2, 2, 2, 2, -1, -1, -1, 2, 2,2, 2,2, 2 ]. \end{align*}
Finally,equation (38) becomes
\begin{align}\label{4.10}
\begin{bmatrix}
R_1\\
R_2\\
\vdots\\
R_6
\end{bmatrix}x=0.
\end{align}
(44)
It is easy to check that the strategy
\begin{align}\label{4.11}
x^*_i(t)=
\begin{cases}
R,& P(R)=\dfrac{1}{3},\\[2mm]
S,& P(S)=\dfrac{1}{3},\\[2mm]
P,& P(C)=\dfrac{1}{3},
\end{cases}\quad i=1,\cdots,3
\end{align}
(45)
In fact,there are infinitely many Nash equilibriums. Algorithm 1 can be used to calculate some of them: Randomly choose an initial point as \begin{align*} &x_1^0=\left[\begin{array}{ccc}0.422&0.298&0.280\end{array}\right]^\mathrm{T},\\ &x_2^0=\left[\begin{array}{ccc}0.468&0.146&0.386\end{array}\right]^\mathrm{T} ,\\ &x_3^0=\left[\begin{array}{ccc}0.443&0.224&0.334\end{array}\right]^\mathrm{T}, \end{align*} then a Nash equilibrium is calculated as \begin{align*} &x_1^*=\left[\begin{array}{ccc}0.303&0.268&0.429\end{array}\right]^\mathrm{T},\\ &x_2^*=\left[\begin{array}{ccc}0.303&0.268&0.429\end{array}\right]^\mathrm{T},\\ &x_3^*=\left[\begin{array}{ccc}0.364&0.398&0.238\end{array}\right]^\mathrm{T}. \end{align*}
Another initial point is chosen as \begin{align*} &x_1^0=\left[\begin{array}{ccc}0.115&0.082&0.803\end{array}\right]^\mathrm{T},\\ &x_2^0=\left[\begin{array}{ccc}0.423&0.507&0.070\end{array}\right]^\mathrm{T} ,\\ &x_3^0=\left[\begin{array}{ccc}0.542&0.447&0.011\end{array}\right]^\mathrm{T}, \end{align*} then the corresponding Nash equilibrium is \begin{align*} &x_1^*=\left[\begin{array}{ccc}0.303&0.268&0.429\end{array}\right]^\mathrm{T},\\ &x_2^*=\left[\begin{array}{ccc}0.303&0.268&0.429\end{array}\right]^\mathrm{T} ,\\ &x_3^*=\left[\begin{array}{ccc}0.364&0.398&0.238\end{array}\right]^\mathrm{T}. \end{align*}
VI. NASH EQUILIBRIUM(S) OF NEGSFirst,we consider the Nash equilibrium of a networked game (NG).
A.Static CaseCombining the results in the last two sections,it is clear that the algorithm developed in Section V can be used directly to find the static Nash equilibrium(s) based on the network profile dynamics obtained in Section IV. But as the size of the network is not small, getting the overall network profile dynamics is a heavy job. In this section,we consider how to get the global Nash equilibrium via the local one.
Let $(N,E)$ be a graph. $(N',E')$ is called a subgraph of $(N,E)$ if 1) $N'\subset N$,$E'\subset E$; and 2) if $(a,b)\in E$ and $a$,$b$ $\in$ $N'$,then $(a,b)\in E'$. Let $((N,E),G,\Pi)$ be an NEG. $(N',E')$ is a subgraph of $(N,E)$. Then $((N',E'),G,\Pi)$ is called a sub-NEG of $((N,E),G,\Pi)$.
Note that subgraph $(N',E')$ is uniquely determined by $N'$. So, we can simply say $N'$ is a subgraph of $(N,E)$. If there is no possible confusion,we can also simply say $N'$ is a sub-NEG of $((N,E),G,\Pi)$.
Now for each $U_i$,$i\in N$,we consider a sub networked static
game. Using Theorem 4 and Algorithm 1,we can find the
equilibrium:
\begin{align}\label{5.1}
e_i=\left\{x_i^*,x_{j,i}^*\big|j\in U_i\backslash\{i\}\right\}.
\end{align}
(46)
${\bf Definition 7.}$ The Nash equilibrium (46),obtained from the neighborhood $U_i$,is called a local Nash equilibrium of the NEG.
The following result is obvious.
${\bf Theorem 5.}$ Assume there exists a set of local Nash
equilibriums
$$
e_i=\left\{x_i^*,x_{j,i}^*\big|j\in U_i\backslash\{i\}\right\},
\quad i=1,\cdots,n,
$$
such that
\begin{align}\label{5.6}
x_{j,i}^*=x_j^*\in e_j,\quad j\in U_i,\ i=1,\cdots,n.
\end{align}
(47)
${\bf Example 5.}$ Consider a cycle network described in Fig. 3. Assume each player plays with its neighbors the game of rock-scissors-paper as in Example 4.
|
Download:
|
| Fig. 3.A cycle network. | |
It is easy to check that the strategy $$ x_i(t)= \begin{cases} R,& P(R)=\dfrac{1}{3},\\[2mm] S,& P(S)=\dfrac{1}{3},\\[2mm] P,& P(C)=\dfrac{1}{3}, \end{cases}\quad i=1,\cdots,n $$ is both local and global Nash equilibrium.
B.Dynamic Case
In the dynamic case,that is,game $G$ is played repeatedly for
infinite times (or for $n$ times),denoted by $G_{\infty}$ (or
$G_n$),we first need payment criteria to verify the Nash
equilibrium. The following criterion is adopted[25]:
\[{E_i} = \sum\limits_{t = 1}^\infty {{\lambda ^t}{E_i}(t),} \]
(48)
An obvious fact is: if profile $\{(x_1^*(t),\cdots,x_n^*(t)|t=1, 2$,$\cdots\}$ is a Nash equilibrium for $G_{\infty}$,then $\{(x_1^*(t),\cdots,x_n^*(t)|$ $1\leq t\leq s\}$ is also the Nash equilibrium for the finite time game $G_{t}$,$1\leq t\leq s$.
Particularly,the initial profile $\{(x_1^*(1)$,$\cdots$, $x_n^*(1)\}$ is a Nash equilibrium for $G_1$,which is considered as a static game.
Assume the SUR is fixed. Based on the above consideration,the following sufficient condition is obvious.
${\bf Proposition 5.}$ $\{(x_1^*(t),\cdots, x_n^*(t)|t=1,2,\cdots\}$ is a Nash equilibrium for $G_{\infty}$, if
1) $x(1)=\ltimes_{j=1}^nx_j^*(1)$ is a Nash equilibrium for the static game $G_{1}$;
2) $x(1)$ is a fixed point for the strategy dynamics
\begin{align}\label{5.8}
x_i(t+1)=M_ix(t),\quad i=1,\cdots,n.
\end{align}
(49)
The following is a trivial example.
${\bf Example 6.}$ Recall Example 4. It was shown there that $$ x^*_i=\left[\frac{1}{3},~\frac{1}{3},~\frac{1}{3}\right]^{\rm T},\quad i=1,2,3 $$ is a Nash equilibrium for the static game of rock-scissors-paper. To see whether it is also the Nash equilibrium,we have to check (49). Using Table VII and the technique demonstrated in Example 2,we can have the strategy dynamics of (49) with \begin{align*} M_1=&\ [ 1,1,1,1,1,1,3,1,3,1,1,2,2,\\ &\ \ 2,2,2,2,2,3,3,3,3,2,2,3,3,3 ],\\[1mm] M_2=&\ [ 1,1,3,1,1,1,3,1,3,1,1,2,1,\\ &\ \ 2,2,2,2,2,3,3,3,3,2,2,3,2,3 ],\\[1mm] M_3=&\ [ 1,1,3,1,2,2,3,3,3,1,1,1,1,\\ &\ \ 2,2,3,2,3,1,1,3,2,2,2,3,2,3 ]. \end{align*}
Then it is ready to verify that $$ x^*=\ltimes_{i=1}^3x^*_i= \Big[\underbrace{\frac{1}{27},\frac{1}{27},\cdots,\frac{1}{27}}_{27}\Big]^{\rm T} $$ is a fixed point of (49). We conclude that $$ x(t)=x^*,\quad t=1,2,\cdots $$ is the Nash equilibrium of the NEG.
VII. CONCLUSIONIn this paper,we first give a detailed explanation for the structure of NEGs. The FEE is introduced and detailed algorithm for profile dynamics is proposed. This part is based on our recent work[19],in which some related techniques have been developed.
The main contribution of this paper is to investigate the Nash equilibrium(s) of NEGs. First,an algorithm is presented to calculate Nash equilibrium(s) of multi-player games. By analyzing the relationship between local and global Nash equilibriums,the above algorithm is applicable to find (one time) static Nash equilibrium(s) for NEGs. Finally,we present a sufficient condition to obtain dynamic Nash equilibrium(s) via static ones. What we did in this paper is a framework. Many problems remain for further investigation,and the technique proposed in this paper seems promissing.
| [1] | Axelrod R. The Evolution of Cooperation. New York:Basic Books, 1984 |
| [2] | Smith J M, Price G R. The logic of animal conflict. Nature, 1973, 246(5427):15-18 |
| [3] | Holme P, Saramäki J. Temporal networks. Physics Reports, 2013, 519(3):97-125 |
| [4] | Lv L, Medo M, Yeung C H, Zhang Y C, Zhang Z K, Zhou T. Recommender systems. Physics Reports, 2012, 519(1):1-49 |
| [5] | Bilbao J M. Cooperative Games on Combinatorial Structures. Boston:Kluwer Acadmic Publisher, 2000 |
| [6] | Branzei R, Dimitrov D, Tijs S. Models in Cooperative Game Theory (2nd edition). Berlin:Springer-Verlag, 2008 |
| [7] | Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature, 2004, 428:643-646 |
| [8] | Nowak M A, May R M. Evolutionary games and spatial chaos. Nature, 1992, 359(6398):826-829 |
| [9] | Santos F C, Santos M D, Pacheco J M. Social diversity promotes the emergence of cooperation in public goods games. Nature, 2008, 454(7201):213-216 |
| [10] | Rong Zhi-Hai, Tang Ming, Wang Xiao-Fan, Wu Zhi-Xi, Yan Gang, Zhou Tiao. Survey on complex networks. Journal of University of Electronic Science and Technology of China, 2012, 41(6):801-807(in Chinese) |
| [11] | Wang Long, Fu Feng, Chen Xiao-Jie, Wang Jing, Li Zhuo-Zheng, Xie Guang-Ming, Chu Tian-Guang. Evolutionary games on complex networks. CAAI Transactions on Intelligent Systems, 2007, 2(2):1-10(in Chinese) |
| [12] | Perc M. Evolution of cooperation on scale-free networks subject to error and attack. New Journal of Physics, 2009, 11:033027 |
| [13] | Szolnoki A, Perc M, Danku Z. Towards effective payoffs in the Prisoner's Dilemma game on scale-free networks. Physica A, 2008, 387(8-9):2075-2082 |
| [14] | Wang Z, Szolnoki A, Perc M. Evolution of public cooperation on interdependent networks:the impact of biased utility functions. EPL, 2012, 97(4):48001 |
| [15] | Wang Z, Szolnoki A, Perc M. Interdependent network reciprocity in evolutionary games. Scientific Reports, 2013, 3:1183 |
| [16] | Perc M, Gardeñes J G, Szolnoki A, Floria L M, Moreno Y. Evolutionary dynamics of group interactions on structured populations:a review. Journal of Royal Society Interface, 2013, 10(80):20120997 |
| [17] | Szabó G, Tõke C. Evolutionary Prisoner's Dilemma game on a square lattice. Physical Review E, 1998, 58(1):69 |
| [18] | Traulsen A, Nowak M A, Pacheco J M. Stochastic dynamics of invasion and fixation. Physical Review E, 2006, 74:011909 |
| [19] | Cheng D Z, He F, Qi H S, Xu T. Modeling, analysis and control of networked evolutionary games. IEEE Transactions on Automatic Control[Online], available:http://lsc.amss.ac.cn/-dcheng/preprint/NTGAME02.pdf |
| [20] | Cheng D Z, Qi H S, Li Z Q. Analysis and Control of Boolean Networks-A Semi-Tensor Product Approach. London:Springer, 2011 |
| [21] | Cheng D Z, Qi H S, Zhao Y. An Introduction to Semi-Tensor Product of Matrices and Its Applications. Singapore:World Scientific, 2012 |
| [22] | Gibbons R. A Primer in Game Theory. Glasgow:Bell and Bain Ltd., 1992 |
| [23] | Xie Zheng. An Introduction to Game Theory. Beijing:Science Press, 2010(in Chinese) |
| [24] | Bazaraa M S, Sherali H D, Shetty C M. Nonlinear Programming-Theory and Algorithms (3rd edition). Hoboken:John Wiley and Sons, 2006 |
| [25] | Pal R, Datta A, Dougherty E R. Optimal infinite-horizon control for probabilistic Boolean networks. IEEE Transactions on Signal Processing, 2006, 54(6):2375-2387 |
 2014, Vol.1
2014, Vol.1